Таким образом, хеш-таблица, построенная по хеш-функции S1 требует при поиске по одному разу каждого слова 89 лишних операций, хеш-таблица, построенная по хеш-функции S2, требует при поиске по одному разу каждого слова 44 лишние операции, а хеш-таблица, построенная по хеш-функции S3 требует 40 лишних операций. Таким образом, наиболее предпочтительная хеш-функция S3.
Задание 3. Работа со структурами данных (коллекциями)

Имеется двусвязный список и число D. Найти в двусвязном списке первое встретившееся число D и перенести элементы перед найденным в обратном порядке в результирующую очередь. Если перед найденным элементом нет чисел, то очередь останется пустой. На форму вывести перенесенные элементы, и затем первый элемент в полученной очереди. Если очередь осталась пустой, то вывести «null».

Исходный контейнер

LinkedList link = new LinkedList();
Результирующий контейнер

Queue Q = new Queue();
Метод для ввода исходных данных

string[] St = textBox1.Text.Split(',');

bool Num;

int num1;

for (int i = 0; i < St.Length; i++)

{

Num = int.TryParse(St[i], out num1);

if (Num) link.AddLast(int.Parse(St[i]));

else MessageBox.Show("Введены не корректные данные");

}

int D = int.Parse(textBox3.Text);


Действия в соответствии с заданием (перенос элементов очереди в список)

LinkedListNode node;

node = link.First;

while (node!= null && node.Value!=D)

node = node.Next;

string Str1;

if (node!=null) node = node.Previous;

string Str = null;

while (node != null)

{

Q.Enqueue(node.Value);

Str1 = node.Value.ToString();

Str = Str + Str1 + ',';

node = node.Previous;

}

Вывод результата на форму

if (Q.Count() != 0) {

int a = Q.Peek();

Str1 =a.ToString();

Str = Str + Str1; }

else Str = "null";
textBox2.Text = Str;

Задание 4. Рекурсивные алгоритмы

Вычислить рекурсивно сумму чисел от 1 до n по формуле sum(n)=sum(n,2)+sum(n-1,2), где n – целое положительное число, sum(n,a)=n+sum(n-a,a), sum(1,2)=1, sum(2,2)=2.
Аргумент n функции sum(n,a) при a=2 уменьшается на каждом шаге на 2. В определенный момент будет вызвана функция sum(1,2)=1 или sum(2,2)=2 (то есть равная 1 аргументу). С этого значения начинаются шаги рекурсивного выхода.

static int Sum(int x, int a)

{

if (x > 2) return Sum(x - a, a) + x;

else return x;

}

Таким образом весь текст консольной программы будет иметь вид:

namespace ConsoleApp1

{

using System;
namespace ConsoleApp3

{

class Program

{

static int Sum(int x, int a)

{

if (x > 2) return Sum(x - a, a) + x;

else return x;

}
static void Main(string[] args)

{

int a = int.Parse(Console.ReadLine());

int S;

if (a > 1) S = Sum(a, 2) + Sum(a - 1, 2);

else S = a;

Console.WriteLine(S.ToString());

}

}

}

}



Задание 5. Деревья поиска

Дерево двоичного поиска для множества чисел S – это размеченное бинарное дерево, каждой вершине которого сопоставлено число из множества S, причем все пометки удовлетворяют следующему простому правилу: «если больше – направо, если меньше - налево».

Сортировка с помощью двоичного дерева — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения из потока (например, файла, сокета или консоли).

Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка O(log(n)). Соответственно, для n объектов сложность будет составлять O(n*log(n)), что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок». Однако, сложность добавления объекта в разбалансированное дерево может достигать O(n), что может привести к общей сложности порядка O(n²).

Бинарное дерево, соответствующее бинарному поиску среди n записей, можно построить следующим образом: при n=0 дерево сводится к узлу 0. В противном случае корневым узлом является 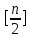, левое поддерево соответствует бинарному дереву с 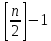узлами, а правое – дереву с 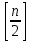узлами и числами в узлах, увеличенными на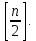

Число узлов, порожденных отельным узлом (число поддеревьев данного корня), называется его степенью. Узел с нулевой степенью называется листом или концевым узлом. Максимальное значение степени всех узлов данного дерева называется степенью дерева.

Алгоритм поиска по бинарному дереву.

Вначале аргумент поиска сравнивается с ключом, находящимся в корне. Если аргумент совпадает с ключом, поиск закончен, если не совпадает, то в случае, когда аргумент оказывается меньше ключа, поиск продолжается в левом поддереве, когда больше ключа – в правом поддереве. Увеличив уровень на 1, повторяют сравнение, считая текущей узел корнем. Исходное множество должно быть упорядочено по возрастанию.

---

Смотрите также файлы

• Практическое задание Каковы, на Ваш взгляд, последствия внедрения профстандартов.docx

• Миссионеры и людоеды.pdf

• биология как наука.docx

• Нгммммщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщщ.docx

• Краткое описание выступления Жукова Кирилла Валерьевича, обучающегося 9 Г класса на защите темы индивидуального итогового проекта Тема проекта.doc