Файл: арифметикалы Жне геометриялы прогрессияларТАырыбын йренгендегі оушыларды ойлау жйесіні алыптасуы таджигитов А. А., Тулебаева А. М.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 13

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

УДК 372. 851
«АРИФМЕТИКАЛЫҚ ЖӘНЕ ГЕОМЕТРИЯЛЫҚ ПРОГРЕССИЯЛАР»ТАҚЫРЫБЫН ҮЙРЕНГЕНДЕГІ ОҚУШЫЛАРДЫҢ ОЙЛАУ ЖҮЙЕСІНІҢ ҚАЛЫПТАСУЫ
Таджигитов А.А., Тулебаева А.М.

(М.Қозыбаев атындағы СҚМУ)

Оқушылардың танымдық іс-әрекетін белсендендіру және ойлау жүйесін жетілдіру педагогиканың мәңгі мәселелерінің бірі болып табылады. К.Д.Ушинский өз еңбектерінде «мектепте баланы ойын-сауық, таңғажайыптармен қызықтырмай, керісінше – оны жағалай айнала қоршаған нәрселерден қызықты нәрсе табуға үйрету керек» деп атап көрсеткен болатын. Қазіргі уақытта да аталған сауал педагогтар мен оқушылардың барлық дәуірлері үшін өзекті болып қалып отыр.

Сонда танымдық белсенділік және ойлау жүйесі дегеніміз нені білдіреді?

Оқу мен шешімді қабылдауы, талдау қабілетің едәуір жылдамдатуы, әлемнің тәжірибелік қабылдау тәсілдерінің бірі – ойлау жүйесі.

А.К Маркова танымдық белсенділіктің көрінісі ретінде «Оқытуға таным ретінде белсенді қараудың барлық түрлерін: оқытудың таным ретіндегі бала үшін мәнінің, мәнділігінің болуын, барлық танымдық уәждердің түрлерін» түсінеді. Оқушылардың танымдық үрдістегі белсенді бастамасын мойындай отырып, ол осының негізінде оқушы оқу қызметінің субъектісі ретінде қалыптасады деп айтады.

П.М Лебедевтің айтуынша, «танымдық белсенділік – оқушылардың білімді меңгеруге деген бастамашыл қарым-қатынасы, сондай-ақ оқыту кезіндегі қызығушылықтың, өзінділіктің және еріктік ынтаның көрінісі» болып табылады.

Жоғарыда аталған анықтамалардың бағыттылығына назар аудару керек: олардың барлығы оқушының ұстанымын сипаттайды, себебі әңгіме оның танымдық белсенділігі мен ойлау қабілеті туралы айтылып отыр. Сонымен бірге танымдық іс-әрекетті белсендендіру – екі жақты үрдіс. Таным үрдісін белсендендіретін шарттарды алдымен мұғалім қалыптастырады, ал осы шарттардың нәтижесін – яғни танымдық белсенділікті көрсететін – оқушы болып табылады.

Танымдық үрдістің өзін кезектескен тізбек ретінде көрсетеді: қабылдау, есте сақтау, сақтау, қайта жандандыру, алынған білімді түсіндіру. Танымды белсендендіру барлық кезектескен кезеңдерде іске асуы мүмкін екендігі белгілі. Бірақ, педагог қалыптастырған шарттарға оқушының жауаптық реакциясы түріндегі белсенділік жағдайы қандай да бір кезеңде де көрінуі мүмкін.

Сонымен, танымдық белсенділікті кейін қалыптасатын, бекитін және ерекше ұйымдасқан танымдық үрдіс кезінде дамитын жекелеген қасиет ретінде анықтауға болады, бұл кезде оқушылардың жеке және жас ерекшеліктері ескерілуі керек.


Орта мектептегі алгебра курсында «Арифметикалық және геометриялық прогрессиялар» тақырыбы оқшау үйретіледі, тек тоғызыншы сыныпта ғана мектеп бағдарламасының басқа тарауларымен аз байланыса отырып оқытылады. Бірақ, п-дік мүшенің формулалары мен алғашқы п мүшелердің қосындысын ғана білуді қажет ететін бұл тапсырмаларға қарамастан, оларды шешу үшін ұлттық бірінғай тесті (ҰБТ) мен жоғары оқу орындарына түсу емтихандарында ұсынылатын арифметикалық және геометриялық прогрессиялардың қасиеттерін де білу керек. Ал оқушылардың білімдері жеткілікті жоғары деңгейде болу үшін, прогрессияны оқыту кезінде оның танымдық іс-әрекетін белсендендіру керек. Сондықтан, аталған тақырып бойынша теориялық және практикалық зерттеулер қазіргі уақытта өзекті болып табылады және әр түрлі деңгейдегі орта мектептердің: жалпы білім беретін, және математикалық бағыттағы күнделікті қажеттіліктерімен ғана шартталған.

Аталған жұмыстың мақсаты «Арифметикалық және геометриялық прогрессиялар» тақырыбын оқушылардың танымдық іс-әрекетін белсендендіру және ойлау жүйесін жүйелеу тұрғысынан оқыту әдістемесін жетілдіру болып табылады.

Қойылған мақсатты іске асыру бірқатар нақты міндеттерді шешуді қажет етті.

  1. Прогрессияларды оқыту әдістемесін оқушылардың танымдық іс-әрекетін белсендендіру негізінде жетілдіру.

  2. Қазіргі уақытта бар арифметикалық және геометриялық прогрессиялардың анықтамаларын, формулалары мен қасиеттерін зерттеу.

  3. «Арифметикалық және геометриялық прогрессиялар» тақырыбын оқу бойынша бүтін теориялық базаны қалыптастыру.

  4. Ұсынылған әдістеменің тиімділігін анықтау мақсатымен практикалық тексеріс жүргізу.

Қойылған міндеттерді шешу үшін келесі әдістер қолданылды:

  1. ғылыми және әдістемелік әдебиеттерді, сондай-ақ оқу құралдарын талдау;

  2. таңдалған теориялық және практикалық материалды мұқият зерттеу және өңдеу;

  3. «Арифметикалық және геометриялық прогрессиялар» тақырыбы бойынша тапсырмаларды шешу;

  4. «Арифметикалық және геометриялық прогрессиялар» тақырыбын оқытудың қолда бар тәжірибесін зерделеу және жалпылау;

Түлектік біліктілік жұмысының практикалық маңыздылығы оны жалпы білім беретін орта мектептің алгебра курсында «Арифметикалық және геометриялық прогрессиялар» тақырыбын оқыту кезінде, сондай-ақ оқушыларды ҰБТ және жоғары оқу орындарына түсу емтихандарын тапсыру кезінде септігін тигізетін ғылыми-әдістемелік құрал ретінде қолданылуы мүмкін екендігімен анықталады.


Сонда арифметикалық және геометриялық прогрессиялар дегеніміз не ? − деген сұрақ туындайды.

Арифметикалық прогрессия деп екіншісінен бастап әрбір мүшесі сол санмен қосылған алдыңғы мүшеге тең болатын жүйе. Ал геометриялық прогрессиядегеніміз нөлден басқа мүшелер жүйесі, ондағы әрбір мүше екіншісінен бастап дәл сол санға көбейтілген алдыңғы мүшеге тең болады.

Прогрессия
Арифметикалық
Геометриялық

Анықтама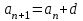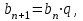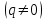




Прогрессияның n-ші мүшесінің формуласы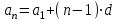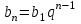




Алғашқы n-ші мүшесінің қосындысын табу формуласы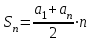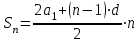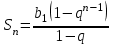






Прогрессиялардың өзіне тән қасиеттері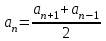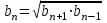




Прогрессияға арналғанесептердің шығару жолы:

1- есеп. 218; 212; 206; 200; 194; ... арифметикалық прогрессияның 122 -мүшесін есептейік.

Шешуі: Бұл прогрессияда 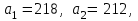демек, .

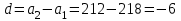Формула бойынш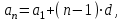а, онда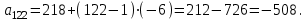

Жауабы:

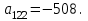
2 – есеп: 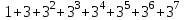өрнегінің қосындысын табыңдар.

Шешуі: Бұл қосынды геометриялық прогрессияның алғашқы сегіз мүшесінің қосындысы болғандықтан, 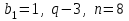және 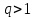екенін ескеріп және алғашқы n – ші мүшесінің формуласын қолдану арқылы 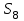-ді таба аламыз, сонда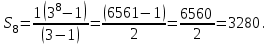


Жауабы:

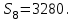
3 – есеп: Қосындысы 15-ке тең арифметикалық прогрессияны құрайтын үш сан берілген. Егер оларға сәйкес 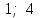және 19 сандарын қосса, онда шыққан үш сан геометриялық прогрессияны құрайды. Берілген сандарды табыңдар.

Шешуі: Есептің шарты бойынша 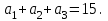Арифметрикалық прогрессия айырымының қасиеті бойынша 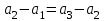, онда 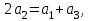сонда 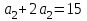болады. Бұдан 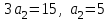. Сонда .

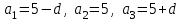Енді әрқайсысына есептің шарты бойынша сәйкес санды қосып, геометриялық прогрессияның мүшелерін аламыз:







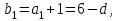
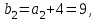
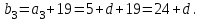
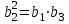теңдеуі бойынша, келесі теңдеуді аламыз: .

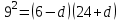Теңдеуді шешсек, 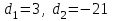шығады. Енді 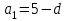теңдігін және шыққан айырымның мәнін қолданып, бірінші мүшені есептейміз, яғни 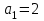немесе 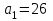. Сонда 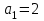және 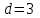болғанда,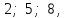
ал немесе 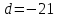болғанда, 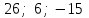сандарын аламыз.

Жауабы: 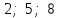және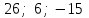

«Тоқсан сөздің тобықтай түйіні»,- демекші мақаламның түйініне келетін болсам.
«Арифметикалық және геометриялық прогресиялар» тақырыбын тереңірек түсіну үшін көптеген арнайы әдебиет қарастырып, қажетті материал жинақтау қажет. Мақаланың мақсаты прогрессиялар теориясын тереңдетіп зерттеу және стандартты емес есептерді шешу үшін оның қосымшалары прогрессиялар туралы оқудағы теориялық материалды жүйелеу және оның практикада қолданылуын көрсету болды.

Соңғы уақытта «Арифметикалық және геометриялық прогрессиялар» тақырыбы кең қолданылуда. Сондықтан бұл тақырып бойынша материалдарды қарастыру өзекті және талап етілуде.
Әдебиет:

  1. Бартенев Ф.А. Нестандартные задачи по алгебре: Пособие для учителей. – М.: Просвещение, 1976. – 95 б.

  2. Әбілқасымова А., Бекбоев И., Абдиев А., Жұмағұлова З., «Алгебра», 9 сынып. Математика. – Алматы:Атамұра, 2006. – 37 б.

  3. Шыныбеков А.Н.,Алгебра, 9 сынып. – Алматы: Атамұра, 2005. – 37 б.

  4. Коротаева Е.В. Обучающие технологии в познавательной деятельности школьников // Библиотека журнала «Директор школы». – 2003. – № 2. – Б. 114 – 153.

Смотрите также файлы