Файл: Задача Получить оптимальный вариант решения транспортной задачи для следующих условий.docx

Скачать файл (0,05Мб)

Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 26

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задача 1.

Получить оптимальный вариант решения транспортной задачи для следующих условий

Пункты потребления		Пункты отправления				Потребность в грузе
Пункты потребления		А₁	А₂	А₃
	U/V
Б₁	0	4	4	2	40
Б₂		2	4	6	180
Б₃		3	2	3	50
Б₄		2	4	2	160
Б₅		6	2	4	170
Наличие груза		210	120	270

Примечание: в правой части каждого прямоугольника указана величина расстояния между соответствующими пунктами.

Решение:

Для решения задачи необходимо выполнение следующего условия:
суммарные запасы продукции у поставщиков должны равняться суммарной потребности потребителей.

Проверим.
Запасы поставщиков: 210 + 120 + 270 = 600 единиц продукции.

Потребность потребителей: 40 + 180 + 50 + 160 + 170 = 600 единиц продукции.

Суммарные запасы продукции у поставщиков равны суммарной потребности потребителей.

Для решения задачи необходимо выполнение следующего условия:
количество задействованных маршрутов = количество поставщиков + количество потребителей - 1.

Поэтому если возникнет ситуация, в которой будет необходимо исключить столбец и строку одновременно, мы исключим что-то одно.

В первую очередь, будем задействовать маршруты с наименьшей стоимостью доставки.

Требуется

составить план перевозок, при котором общая стоимость доставки продукции

Поставщик	Потребитель					Запас
Поставщик	B ₁	B ₂	B ₃	B ₄	B ₅	Запас
A ₁	4	180 2	30 3	2	6	~~210~~ 30 нет
A ₂	4	4	2	4	120 2	~~120~~ нет
A ₃	40 2	6	20 3	160 2	50 4	~~270~~ ~~110~~ 70 50 нет
Потребность	40 нет	~~180~~ нет	50 20 нет	~~160~~ нет	~~170~~ 50 нет

Стоимость доставки продукции, для начального решения, не сложно посчитать.

1802 + 303 + 1202 + 402 + 203 + 1602 + 50*4 = 1350 ден. ед.

Полученное решение является оптимальным?

Проверим.

Каждому поставщику A _i ставим в соответствие некоторое число U _i, называемое потенциалом поставщика.
Каждому потребителю B _j ставим в соответствие некоторое число V _j , называемое потенциалом потребителя.

Для задействованного маршрута:

потенциал поставщика + потенциал потребителя = тариф задействованного маршрута.

Последовательно найдем значения потенциалов.
Значение одного потенциала необходимо задать. Пусть u₁ = 0.

Поставщик

Потребитель

B ₁

B ₂

B ₃

B ₄

B ₅

A ₁

180

2

30

3

u₁ = 0

A ₂

120

2

u₂ = -2

A ₃

40

2

20

3

160

2

50

4

u₃ = 0

v₁ = 2

v₂ = 2

v₃ = 3

v₄ = 2

v₅ = 4

A₃B₁:	v₁ + u₃ = 2	v₁ = 2 - 0 = 2
A₃B₃:	v₃ + u₃ = 3	v₃ = 3 - 0 = 3
A₃B₄:	v₄ + u₃ = 2	v₄ = 2 - 0 = 2
A₃B₅:	v₅ + u₃ = 4	v₅ = 4 - 0 = 4
A₁B₃:	v₃ + u₁ = 3	u₁ = 3 - 3 = 0
A₂B₅:	v₅ + u₂ = 2	u₂ = 2 - 4 = -2
A₁B₂:	v₂ + u₁ = 2	v₂ = 2 - 0 = 2

Найдем оценки незадействованных маршрутов (c_ij - стоимость доставки).

A₁B₁ :	Δ₁₁ = c₁₁ - ( u₁ + v₁ ) = 4 - ( 0 + 2 ) = 2
A₁B₄ :	Δ₁₄ = c₁₄ - ( u₁ + v₄ ) = 2 - ( 0 + 2 ) = 0
A₁B₅ :	Δ₁₅ = c₁₅ - ( u₁ + v₅ ) = 6 - ( 0 + 4 ) = 2
A₂B₁ :	Δ₂₁ = c₂₁ - ( u₂ + v₁ ) = 4 - ( -2 + 2 ) = 4
A₂B₂ :	Δ₂₂ = c₂₂ - ( u₂ + v₂ ) = 4 - ( -2 + 2 ) = 4
A₂B₃ :	Δ₂₃ = c₂₃ - ( u₂ + v₃ ) = 2 - ( -2 + 3 ) = 1
A₂B₄ :	Δ₂₄ = c₂₄ - ( u₂ + v₄ ) = 4 - ( -2 + 2 ) = 4
A₃B₂ :	Δ₃₂ = c₃₂ - ( u₃ + v₂ ) = 6 - ( 0 + 2 ) = 4

Нет отрицательных оценок. Следовательно, уменьшить общую стоимость доставки продукции невозможно.

Ответ: S_min = 1350 ден. ед.

Задача 2.

Для вывозки зерна из сельской местности на элеватор требуется 10 автомобилей MAN TGS 33.360 (грузоподъемность – 20т), работающих по 14 часов ежедневно. На сколько сократится необходимое количе6ство автомобилей, если пункты будут оборудованы современными средствами механизации, и время погрузки и разгрузки одного автомобиля сократится с 0,8 ч до 0,5 ч? Расстояние ездки с грузом – 20 км, коэффициент использования пробега за ездку – 0,5, коэффициент использования грузоподъемности 1,0, техническая скорость – 30 км/ч, нулевой пробег каждого автомобиля в день – 5 км.

Решение

-время, затрачиваемое на одну поездку до сокращения времени погрузки-разгрузки:

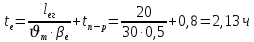
-время нулевого пробега:

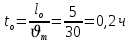
- время работы на маршруте:

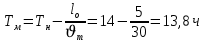
-число ездок за рабочий день:

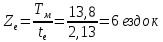
- производительность автопоезда грузоподъемностью q_H= 20 т за день:

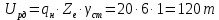
Потребность в подвижном составе для работы на линии:

-число автомобилей в эксплуатации:

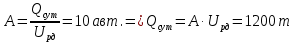
-время, затрачиваемое на одну поездку после сокращения времени погрузки-разгрузки:

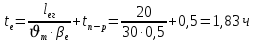
-число ездок за рабочий день:

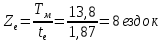
- производительность автопоезда грузоподъемностью q_H= 20 т за день:

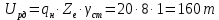
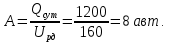
Определяем:

насколько уменьшится потребность в подвижном составе:

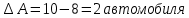
Ответ:необходимое количество автомобилей сократиться на 2 единицы.

Задача 3.

Интервал движения автобусов на городском тангенциальном маршруте составляет 4 мин. Количество промежуточных остановок на маршруте – 12. Время простоя автобуса на каждой промежуточной остановке – 20 с. Техническая скорость – 24 км/ч. Скорость сообщения 20 км/ч. Эксплуатационная скорость – 16 км/ч. Сколько автобусов работает на маршруте?

Задача 4.

Годовой объем перевозок тарно-упаковочных грузов в контейнерах – 11520 т. Средняя грузоподъемность одного контейнера – 1 т. Коэффициент использования грузоподъемности контейнера – 0,8. Время оборота контейнера – 10 дней. Количество дней работы погрузочно-разгрузочных пунктов – 360. Определить потребное количество контейнеров.

Решение

- потребное количество контейнеров:

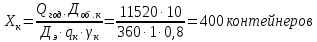
Ответ:необходимое количество контейнеров – 400.
Задача 5.

Построить эпюру групотоков для автомобильной линии с конечными пунктами А и В. Промежуточные пункты С и Д. Величины грузопотоков ( в тоннах) между пунктами даны в таблице.

Пункты отправления	Пункты получения
Пункты отправления	А	С	Д	В
А С Д В	- 2100 800 600	1100 - 1000 800	500 1800 - 1700	200 900 900 -