Файл: Левченко Ирина Анатольевна Место работы гоу лнр Перевальская гимназия 1 общая информация по уроку класс укажите класс, к которому относится урок.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа: разработка технологической карты урока
Инструкция по выполнению практической работы: выберите класс, тему урока в соответствии с ПРП и заполните представленную ниже таблицу. Для каждого учебного задания, включенного в урок, укажите планируемые результаты, на достижение которых это задание направлено.
1. ИНФОРМАЦИЯ О РАЗРАБОТЧИКЕ ПЛАНА
| ФИО разработчика | Левченко Ирина Анатольевна |
| Место работы | ГОУ ЛНР «Перевальская гимназия №1» |
2. ОБЩАЯ ИНФОРМАЦИЯ ПО УРОКУ
| Класс (укажите класс, к которому относится урок): | 8 класс (геометрия) |
| Место урока (по тематическому планированию ПРП) | 26 (II четверть) |
| Тема урока | Применение теоремы Пифагора при решении задач |
| Уровень изучения (укажите один или оба уровня изучения (базовый, углубленный), на которые рассчитан урок): | базовый уровень |
| Тип урока (укажите тип урока): | +☐ урок-закрепление |
| Планируемые результаты (по ПРП): | |
| Личностные: понимание математической науки как сферы человеческой деятельности, этапов её развития и значимости для развития цивилизации; овладение языком математики и математической культурой как средством познания мира; овладение простейшими навыками исследовательской деятельности. | |
| Метапредметные: — работа над понятием информация-знание; — выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев); — выбирать форму представления информации и иллюстрировать решаемые задачи схемами. | |
| Предметные: — закрепить знание теоремы Пифагора; — понимать, как найти неизвестную сторону прямоугольного треугольника при помощи теоремы Пифагора; — уметь применять полученные знания при решении практических задач. | |
| Ключевые слова (введите через запятую список ключевых слов, характеризующих урок): прямоугольный треугольник, катет, гипотенуза, теорема Пифагора, пифагоровы треугольники, египетский треугольник | |
| Краткое описание (введите аннотацию к уроку, укажите используемые материалы/оборудование/электронные образовательные ресурсы): учебник: Геометрия 7–9 классы: учеб. для общеобразоват. организаций / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.] — 6-е изд. — М. : Просвещение, 2016. — 383 с.: ил. сборник ОГЭ: Математика. Подготовка к ОГЭ-2023. 9-й класс. 40 тренировочных вариантов по демоверсии 2023 года: учебно-методическое пособие / под ред. Ф. Ф. Лысенко, С. О. Иванова. — Ростов н/Д: Легион, 2022. — 368с. — (ОГЭ). карточки с заданием, тетрадь, чертежные инструменты | |
3. БЛОЧНО-МОДУЛЬНОЕ ОПИСАНИЕ УРОКА
| БЛОК 1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала |
| Этап 1.1. Мотивирование на учебную деятельность |
| Укажите формы организации учебной деятельности на данном этапе урока. Опишите конкретную учебную установку, вопрос, задание, интересный факт, которые мотивируют мыслительную деятельность школьника (это интересно/знаешь ли ты, что) |
| Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. Сообщение темы урока. Здравствуйте, ребята! На прошлом уроке мы с вами выучили теорему Пифагора, ее доказательство. Сегодня мы закрепим знания, решая задачи с помощью данной теоремы. В качестве домашнего задания вы должны были подготовить коротенькие сообщения о том, где в современном мире используется теорема Пифагора. Примерные ответы детей: Окна. В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. По теореме Пифагора рассчитывается длина такого ребра, как гипотенуза прямоугольного треугольника. Строительство крыши. При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. При проектировании любых строительных объектов возникает необходимость вычислять стороны прямоугольных треугольников по известным сторонам. Подобные задачи решаются в нашей повседневной жизни. Молниеотвод. Гроза и ее непременный атрибут молния – атмосферное явление, таящее в себе достаточно большую опасность. Достаточно сказать, что в год в мире от удара молнии гибнет более 3000 человек. Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту также помогает теорема Пифагора. Мобильная связь. В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, радиусе R = 200 км, если известно, что радиус Земли равен 6380 км). Эта задача также решается при помощи теоремы Пифагора. Планируемые результаты. Коммуникативные: начинают сотрудничество с учителем и сверстниками. Регулятивные: умеют мобилизовать свои силы. Личностные: мотивация учения. |
| Этап 1.2. Актуализация опорных знаний |
| Укажите формы организации учебной деятельности и учебные задания для актуализации опорных знаний, необходимых для изучения нового |
| Прежде чем начать наш урок, повторим основное. Устно ответьте на вопросы: 1.Какой треугольник называется прямоугольным? 2 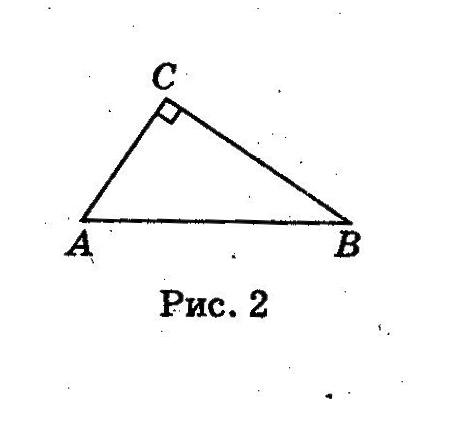 . Как называются его стороны? 3. Что такое гипотенуза? 4. Что такое катет? 5. Назовите, пользуясь рисунком, гипотенузу и катет. 6. Как найти площадь прямоугольного треугольника? 7. Что такое квадрат? 8. Как найти его площадь? 9. Сторона квадрата 8 м. Найдите его площадь. Планируемые результаты. Познавательные: структурируют собственные знания. Коммуникативные: выражают свои мысли с достаточной полнотой и точностью; слушают и понимают речь других. Регулятивные: контролируют и оценивают процесс и результаты деятельности. Личностные: оценивают уровень усвоенного им материала. |
| Этап 1.3. Целеполагание |
| Назовите цель (стратегия успеха): ты узнаешь, ты научишься |
| Во время нашего урока мы с вами закрепим как связаны между собой стороны прямоугольного треугольника; отработаем умения находить третью сторону, если известны две другие стороны прямоугольного треугольника. |
| БЛОК 2. Освоение нового материала |
| Этап 2.1. Осуществление учебных действий по освоению нового материала |
| Укажите формы организации учебной деятельности, включая самостоятельную учебную деятельность учащихся (изучаем новое/открываем новое). Приведите учебные задания для самостоятельной работы с учебником, электронными образовательными материалам (рекомендуется обратить внимание учеников на необходимость двукратного прочтения, просмотра, прослушивания материала. 1) на общее понимание и мотивацию 2) на детали). Приведите задания по составлению плана, тезисов, резюме, аннотации, презентаций; по наблюдению за процессами, их объяснением, проведению эксперимента и интерпретации результатов, по построению гипотезы на основе анализа имеющихся данных и т.д. |
| Формы работы: фронтальная, индивидуальная, работа в парах, работа в группах. Проверить знание формулировки теоремы Пифагора в ходе устного опроса. |
| Этап 2.2. Проверка первичного усвоения |
| Укажите виды учебной деятельности, используйте соответствующие методические приемы. (Сформулируйте/Изложите факты/Проверьте себя/Дайте определение понятию/Установите, что (где, когда)/Сформулируйте главное (тезис, мысль, правило, закон) |
| А теперь давайте проверим ваши знания на практике. На доске вы видите задачи на рисунках. Три человека решают у доски, остальные в тетрадях. 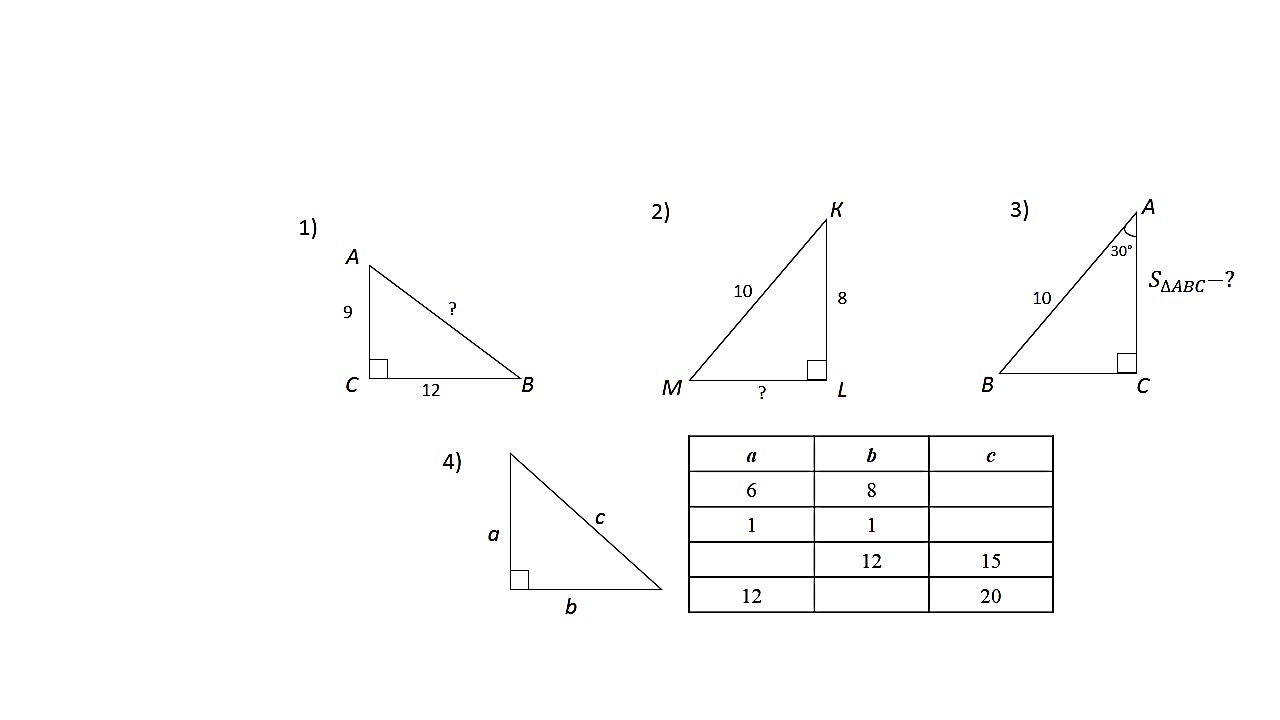 Планируемые результаты. Коммуникативные: умеют вступать в диалог, участвуют в коллективном обсуждении вопроса. Познавательные: строят логической цепи рассуждений, выдвигают гипотезы и их обоснование. Предметные: умеют применять теорему Пифагора для решения задач. Личностные: формирование готовности к самообразованию. |
| БЛОК 3. Применение изученного материала |
| Этап 3.1. Применение знаний, в том числе в новых ситуациях |
| Укажите формы организации соответствующего этапа урока. Предложите виды деятельности (решение задач, выполнение заданий, выполнение лабораторных работ, выполнение работ практикума, проведение исследовательского эксперимента, моделирование и конструирование и пр.), используйте соответствующие методические приемы (используй правило/закон/формулу/теорию/идею/принцип и т.д.; докажите истинность/ложность утверждения и т.д.; аргументируйте собственное мнение; выполните задание; решите задачу; выполните/сделайте практическую/лабораторную работу и т.д.). |
| У 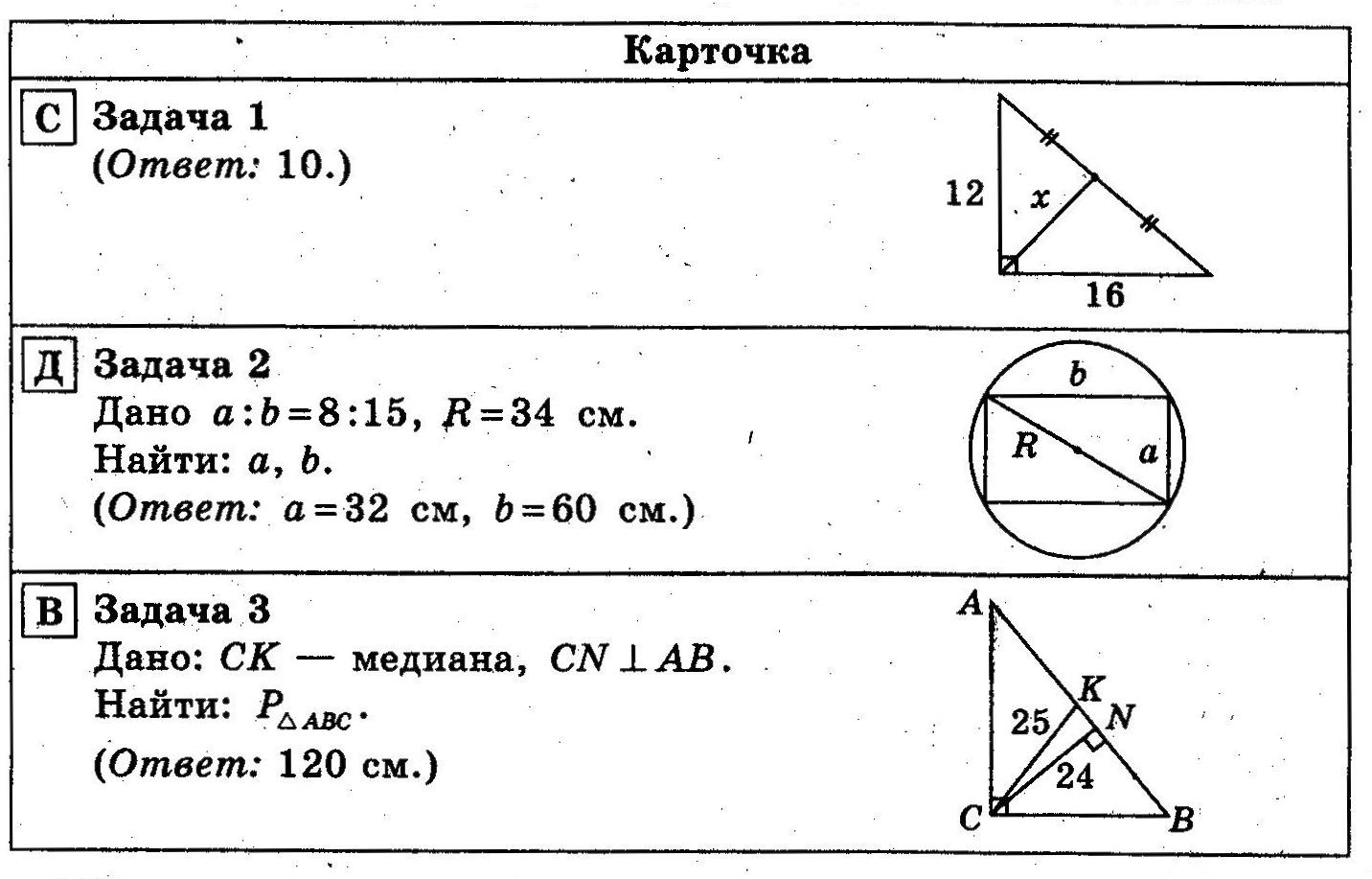 чащиеся объединяются в группы однородного состава и решают задания на карточках по готовым чертежам. Внутри группы учащиеся делятся тоже на 3 группы, и каждая такая «маленькая» группа решает по одной задаче. Потом они обмениваются решениями. Учитель вызывает учащихся для комментария решений. Планируемые результаты. Коммуникативные: работают в группе: находят общее решение; слушают партнёра; формулируют, аргументируют и отстаивают своё мнение. Познавательные: построение логической цепи рассуждений, выдвижение гипотез и их обоснование. Регулятивные: умеют ясно, точно, грамотно излагать свои мысли в устной и письменной речи. |
| Этап 3.2. Выполнение межпредметных заданий и заданий из реальной жизни |
| Подберите соответствующие учебные задания |
| Давайте решим задачу, с которой может столкнуться каждый. (Один ученик решает у доски, остальные в тетради). На какое расстояние следует отодвинуть от стены дома нижний конец лестницы, длина которой 13 м, чтобы верхний ее конец оказался на высоте 12 м? Планируемые результаты. Предметные: умеют применять теорему Пифагора для решения задач. Личностные: формирование готовности к самообразованию. Познавательные: понимают и используют математические средства наглядности (чертежи.) для иллюстрации, интерпретации, аргументации. |
| Этап 3.3. Выполнение заданий в формате ГИА (ОГЭ, ЕГЭ) |
| Подберите соответствующие учебные задания |
| А теперь давайте с вами решим задачи из сборника ОГЭ. (Один ученик решает у доски, остальные в тетради). Вариант 9, № 23. Катеты прямоугольного треугольника равны 12 и 16. Найдите высоту, проведенную к гипотенузе. Планируемые результаты. Личностные: формирование готовности к самообразованию. Познавательные: находят в различных источниках информацию, необходимую для решения математических проблем. Регулятивные: выбирает действия в соответствии с поставленной задачей и условиями её реализации. |
| Этап 3.4. Развитие функциональной грамотности |
| Подберите соответствующие учебные задания |
| Давайте решим с вами следующие задачи. (Два ученика решают у доски, остальные в тетради). Задача 1. 12 апреля 1961 года Ю.А.Гагарин на космическом корабле «Восток» был поднят над землёй на максимальную высоту 327 км. На каком расстоянии от земли от корабля находился в это время наиболее удаленные от него и видимые космонавтом участники поверхности Земли? (Радиус Земли считать равным 6400 км.) Задача 2. От пристани одновременно отплыли два парохода: один на юг со скоростью 16 морских миль в час, а другой на запад со скоростью 12 морских миль в час. Какое расстояние будет между пароходами через 2,5 ч.(1 морская миля=1,85 км.) Планируемые результаты. Личностные: формирование готовности к самообразованию. Познавательные: находят в различных источниках информацию, необходимую для решения математических проблем. Регулятивные: выбирают действия в соответствии с поставленной задачей и условиями её реализации. |
| Этап 3.5. Систематизация знаний и умений |
| Подберите учебные задания на выявление связи изученной на уроке темы с освоенным ранее материалом/другими предметами |
| Решение задач из учебника: № 487, 493. (Два ученика решают у доски, остальные в тетради). № 487. Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 см. Найдите высоту, проведённую к основанию. № 493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см. Планируемые результаты. Регулятивные: адекватно оценивают правильность или ошибочность выполнения учебной задачи. Познавательные: строят логические рассуждения. Личностные: формирование готовности к самообразованию. |
| БЛОК 4. Проверка приобретенных знаний, умений и навыков |
| Этап 4.1. Диагностика/самодиагностика |
| Укажите формы организации и поддержки самостоятельной учебной деятельности ученика, критерии оценивания |
| К каждому заданию на уроке формируются четкие критерии, по которым учащиеся могут сами объективно оценить результат своей работы. |
| БЛОК 5. Подведение итогов, домашнее задание |
| Этап 5.1. Рефлексия |
| Введите рекомендации для учителя по организации в классе рефлексии по достигнутым либо недостигнутым образовательным результатам |
| Учащиеся анализируют свою работу и заканчивают ответ Я узнал…. Я научился… Теперь я умею ... Мне понравилось … Было трудно… Мне показалось важным… |
| Этап 5.2. Домашнее задание |
| Введите рекомендации по домашнему заданию. |
| Повторите пар. 3, п. 55-56, решите задачи: 1. Найдите сторону ромба, если его диагонали равны 12 см и 16 см. 2. Основания равнобокой трапеции равны 21 см и 37 см, а боковая сторона – 10 см. Найдите высоту трапеции. Напоминаю, что к каждой задаче должен быть выполнен рисунок. Планируемые результаты. Личностные: повышение внутренней мотивации. Регулятивные: способны к аналитическим действиям. Коммуникативные: умеют аргументировать свой ответ. Познавательные: умеют ориентироваться в своей системе знаний. |