ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Класс: 8 Урок №_____ Дата__________
Тема урока: Неравенства
Цель урока: совершенствовать навыки решения неравенств и систем неравенств; рассмотреть более сложные задания; проверить знания и умения учащихся по данной теме.
Планируемые результаты:
обучающиеся должны знать:
- понятия: «числовое неравенство», «неравенство с переменной», «решение неравенства с переменной», «линейное неравенство», «равносильное неравенство», «равносильное преобразование неравенства», «правила для решения неравенств»
обучающиеся должны уметь:
- решать линейные неравенства и отображать множество его решений на координатной прямой.
Личностные: планировать свои действия в соответствии с учебным заданием.
Метапредметные: формировать умение создавать обобщения, устанавливать аналогии, классифицировать.
Тип урока: повторение
Оборудование: учебник, карточки
ХОД УРОКА
Содержание урока
I. Организационный момент (Приветствие учителя.Вопросы при необходимости).
II. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Дорогие ребята! Сегодня на уроке мы должны обобщить, систематизировать и проверить знания, умения и навыки в процессе решения неравенств и их систем.
Чтобы легче всем жилось,
Чтоб решалось, чтоб моглось,
Улыбнись, удача, всем,
Чтобы не было проблем.
Открываем тетради и проверяем правильность выполнения домашних заданий.
III. Актуализация знаний.
Проверка домашнего задания.
№ 849 (а, д, ж, з, и).
Р е ш е н и е
а)
> 1; ∙ 5 > 1 ∙ 5; 2x> 5;
x> 5 : 2;
x> 2,5.
д) 2 >
; 2 ∙ 5 >
∙ 5; 10 > 6 – x;
x> 6 – 10;
x> –4.
ж)
≥ 0; ∙ 42 ≥ 0 ∙ 42; 12 – 7x ≥ 0;
–7x ≥ –12;
х ≤ (–12) : (–7);
х ≤
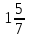
з)
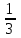(х + 15) > 4; 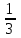(х + 15) ∙ 3 > 4 ∙ 3; х + 15 > 12;
x> 12 – 15;
х> – 3.
и) 6 ≤
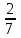(х + 4); 6 ∙ 7 ≤
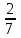(х + 4) ∙ 7; 42 ≤ 2х + 8;
–2x ≤ 8 – 42;
–2x ≤ –34;
х ≥ 17.
О т в е т: а) х> 2,5; д) х> –4; ж)х ≤
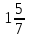; з) х> –3; и) х ≥ 17.№ 851 (а, в).
Р е ш е н и е
| а)  ;2(7 – 2у) > 3у – 7; 14 – 4у> 3у – 7; –4у – 3у> –14 – 7; –7у> –21; у< (–21) : (–7); у< 3. | б) 5y – 1 > 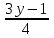 ;4(5y – 1) > 3y – 1; 20y – 4 > 3y – 1; 20y – 3y> 4 – 1; 17y> 3; y>  . |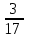
О т в е т: а) при у< 3; в) при y>
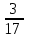.Устный счет.
1. Укажите все целые числа, принадлежащие промежутку: [-4; 4];
Укажите какое – либо число, принадлежащее промежутку (3,5; 3,6 ) ;
Принадлежит ли промежутку [8; 41] число 40,9 ? (слайд)
2. Какие неравенства соответствуют промежуткам:
;
;
;
; 
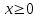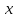<5; -3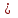
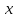<5;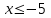 
? (слайд).3. Изобразите геометрическую модель промежутков:
.(слайд)IV . Обобщение и систематизация знаний.
Прочитайте название нашей новой темы: ваши предположения «Что значит -решить неравенство?»
Верно: Решить неравенство – найти значение переменной,
которое обращает его в верное числовое неравенство.
Существуют правила решения неравенств:
-
Если из одной части неравенства перенести в другую слагаемое с противоположным знаком. То получится равносильное ему неравенство. (разбор правила по презентации) -
А) Если обе части неравенства умножить или разделить на одно и тоже положительное число, то получится равносильное ему неравенство.
Б) А как же быть, если необходимо разделить на отрицательное число? Ответ на этот вопрос вы получите разобрав пример № 2 в учебнике на стр, 178.
(ответы учащихся) верно (разбор примера презентации)
Итак, при делении (умножении) на отрицательное число знак неравенства меняется на противоположный.
V. Первичное закрепление:
Решите неравенство:
а)
;
б)
;
(слайд).Работа с учебником.
№ 883 (б, г), № 884 (б).
Р е ш е н и е
№ 883.
б) Допустимы те значения переменной, при которых подкоренные выражения неотрицательны:
; 
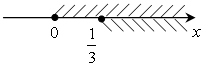.г)
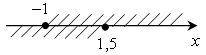; [–1; 1,5].О т в е т: б)
; г) [–1; 1,5].№ 884.
б) В область определения функции y =
входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.
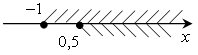
Знаменатель равен нулю, если:
=
;2х – 1 = х + 1;
2х – х = 1 + 1;
х = 2.
Значит, из области определения функции необходимо исключить х = 2.
; [0,5; 2) 
(2; +∞).О т в е т: [0,5; 2)
(2; +∞).3. № 886 (б, г).
Р е ш е н и е
б)
; (0,1; +∞).г)
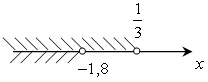; (–∞; –1,8).О т в е т: б) (0,1; +∞); г) (–∞; –1,8).
VI. Информация о домашнем задании.:
№ 836 (д), № 837 (а,б) , № 840 (а,б).
VIII. Подведение итогов: Что значит «Решить неравенство с одной переменной»
1 правило решения неравенств? 2 правило решения неравенств?
Оценка деятельности учащихся. (учителем)
IX. Рефлексия:
| Урок | Я на уроке | Итог |
| 1. интересно | 1. работал | 1. понял материал |
| 2. скучно | 2. отдыхал | 2. узнал больше, чем знал |
| 3.безразлично | 3.помогал другим | 3.не понял |
Спасибо за урок .