ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 310
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ОГЭ по математике. 2022
Тренировочный вариант №5. Шины
Часть 1
Ответами к заданиям 1–19 являются число или последовательность цифр, которыеследуетзаписатьв БЛАНКОТВЕТОВ № 1справаотномера соответствующегозадания, начиная с первой клеточки. Если ответом является последовательностьцифр,тозапишите еёбезпробеловидругихдополнительныхсимволов.Каждыйсимволпишитевотдельнойклеточкевсоответствиисприведённымивбланкеобразцами.
Прочитайтевнимательнотекстивыполнитезадания1–5.

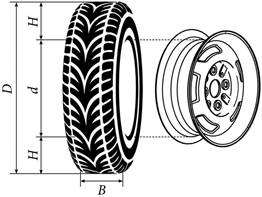
Рис. 1 Рис. 2
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр Hна

рисунке 2) к ширине шины, то есть
????
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса Dлегко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит внедорожники определённой модели и устанавливает на них колёса с шинами маркировки 215/65 R16.
1
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
-
Ширина шины (мм)
Диаметр диска (дюймы)
16
17
18
215
215/65
215/60
–
225
225/65; 225/60
225/55
–
235
235/60
235/55; 235/50
235/50
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.
Ответ:.
2
На сколько миллиметров радиус колеса с шиной маркировки 215/55 R17 меньше, чем радиус колеса с шиной маркировки 275/50 R17?
Ответ:.
3
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 235/50 R18?
Ответ:.
4
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах. Ответ:.
5
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 225/65 R16? Результат округлите до десятых.
Ответ:.
6

Найдите значение выражения
(
7
На координатной прямой отмечены точки A,B,C, и D.
 Одна из них соответствует числу 107. Какая это точка?
Одна из них соответствует числу 107. Какая это точка?13
1) А 2) В 3) С 4) D
Ответ:.

8
 Найдите значение выражения √16????18
Найдите значение выражения √16????18 ????14
при ???? = 3.
Ответ:.
9
Решите уравнение (???? + 10)(− ???? − 8) = 0.
Если уравнеyие имеет более одного корня, в ответ запишите больший из корней. Ответ:.
10
На экзамене 30 билетов, Серёжа не выучил 9 из них. Найдите вероятность того, что ему попадётся выученный билет.
Ответ:.
11
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ГРАФИКИ
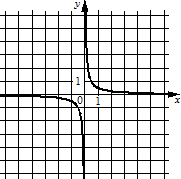
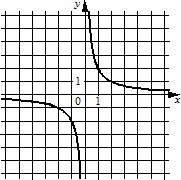
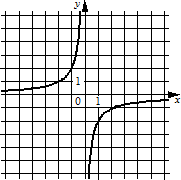 1) 2) 3)
1) 2) 3)ФОРМУЛЫ
 А) ???? = 2
А) ???? = 2????
Б) ???? = 1
 2????
2????В) ???? = − 2
 ????
????| А | Б | В |
| | | |
В таблице под каждой буквой укажите соответствующий номер: Ответ:
12
Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I — сила тока (в амперах), R— сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R, если мощность составляет 98 Вт, а сила тока равна 7 А. Ответ дайте в омах.
Ответ:.
13
Укажите системы неравенств
{???? + 4 ≥ −3,4
???? + 5 ≤ 0
1) [−7,4; −5] 3) (−∞; −7,4]
2) [−5; +∞) 4) (−∞; −7,4] ???? [−5; +∞)
Ответ:.
14
При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 9° C. Найдите температуру вещества (в градусах Цельсия) через 6 минут после начала проведения опыта, если его начальная температура составляла − 6° C .
 Ответ:.
Ответ:.
15
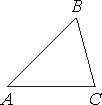
В треугольнике АВС угол А равен 45°, угол В равен 60°, ВС=4√6. Найдите АС.
Ответ:.
16
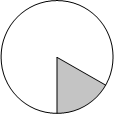
Площадь круга равна 112. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Ответ:.
17
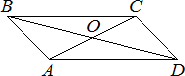
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=8, BD=14, AB=5. Найдите DO.
Ответ:.
18
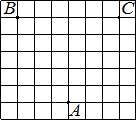
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.
19
Ответ:. Какое из следующих утверждений верно?
-
Треугольник со сторонами 1, 2, 4 существует. -
Если диагонали параллелограмма равны, то этот параллелограмм является ромбом. -
Основания любой трапеции параллельны.
В ответ запишите номер выбранного утверждения. Ответ:.
Часть 2.
Привыполнениизаданий20–25используйтеБЛАНКОТВЕТОВ№2.Сначалаукажите номер задания, а затем запишите его решение и ответ. Пишите чётко иразборчиво.
20
Решите уравнение ????(????2 + 4???? + 4) = 3(???? + 2).
21
Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
22
Постройте график функции ???? = 2,5|????|−1.
|????|−2,5????2
Определите, при каких значениях ???? прямая ???? = ???????? не имеет с графиком общих точек.
23
Высота AH ромба ABCD делит сторону CD на отрезки DH=12 и CH=3. Найдите высоту ромба.
24
Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
25
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Ответы:
-
1.
235
2.
19,25
3.
6,3
4.
685,9
5.
1,9
6.
70,5
7.
1
8.
36
9.
-8
10.
0,7
11.
132
12.
2
13.
1
14.
-60
15.
12
16.
14
17.
7
18.
5
19.
3
20.
-3; -2; 1
21.
11 кг
22.
0; ±6,25
23.
9
24.
-
25.
1,6