Файл: Контрольная работа по дисциплине Логика студент группы 666 пвв проверила Минск 2023 содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
БЕЛЕТ
Кафедра «Информационные технологии в управлении»
Контрольная работа
по дисциплине: «Логика»
Выполнил: студент группы 666
ПВВ
Проверила:
Минск 2023
СОДЕРЖАНИЕ
| Введение | 3 | |
| 1. | Понятие логического закона | 4 |
| 2. | Основные логические законы | 7 |
| 3. | Понимание законов мышления в математической логике | 10 |
| Заключение | 12 | |
| Список использованной литературы | 13 | |
ВВЕДЕНИЕ
Рассматривая вопрос о предмете той или иной науки, нельзя обойтись без выяснения специфики её законов. Это относится и к логике.
Любое высказывание может быть оценено как истинное или ложное. Однако способы установления истинности или ложности высказываний разных типов могут существенно отличаться друг от друга. В некоторых случаях значения высказываний устанавливают путем непосредственного обращения к действительности. В других случаях оценка высказываний осуществляется в рамках конкретных научных теорий. Однако для определенного класса высказываний вопрос об их истинности или ложности может быть решен с использованием исключительно логических средств, на основе анализа их логических форм.
В этой работе предпринимается попытка сформировать понятие о логическом законе, его основных видах. Также затрагивается тема законов мышления в математической логике.
-
Понятие логического закона
Как было упомянуто выше, вопрос об истинности или ложности решается логическими средствами.
Для демонстрации этого способа используем следующее высказывание: «Идёт дождь, или неверно, что идёт дождь».
Заменяя параметром p высказывание «Идёт дождь», получаем логическую форму высказывания: «p или неверно, что p».
В данном высказывании имеет место два положения дел: ситуация, описанная в p, или отсутствие такой ситуации. Здесь используются логические термины «или» и «неверно, что» - они представляют логическое содержание. Это содержание, дополненное содержанием высказывания «Идёт дождь», образует конкретное содержание.
Подставляя вместо p истинное или ложное высказывание, мы в любом случае получаем истинное высказывание. Истинность высказывания обусловлена его логической формой.
Высказывания, истинные в силу своей логической формы, называют логически истинными. Сами же логические формы таких высказываний, зафиксированные в языке, содержащем параметры, называют логическими законами.
Логический закон – это такая логическая форма высказывания, которая принимает значение «истина» при любой интерпретации параметров, входящих в её состав [2, с.31].
Кроме логически истинных существует еще один тип высказываний, значения которых можно установить, основываясь только на анализе их логических форм. Это логически ложные высказывания. Их логические формы принимают значение «ложь» при любой интерпретации параметров в их составе.
Модифицируя пример выше, получаем: «Идёт дождь, и неверно, что идёт дождь».
Его логическая форма: p и неверно, что p.
Очевидно, что в результате подстановки вместо параметры p в форму произвольного высказывания обязательно получится ложное высказывание. Поэтому это высказывание ложно в силу своей логической формы.
Высказывания, которые не являются ни логически истинными, ни логически ложными, называют логически недетерминированными. Их значения невозможно установить, пользуясь исключительно логическими средствами, поскольку некоторые высказывания такой формы истинны, а некоторые ложны.
Пример логически недетерминированного высказывания: «Идёт дождь или светит Солнце».
Его логическая форма: p или q, где p – «Идёт дождь», q – «Светит Солнце».
Если при интерпретации параметров p и q вместо какого-нибудь из них подставить истинное высказывание, то выражение превратится в истинное высказывание. Если же и вместо p, и вместо q подставить ложные высказывания, то получится ложное выражение.
Логическая форма может выявляться с разной степенью глубины. Для решения вопроса о том, является ли некоторое высказывание логически истинным, нужен соответствующий уровень анализа при выявлении его формы.
Пример: «Всякий школьник не остроумен, или некоторые школьники остроумны».
Данное высказывание состоит из двух отличных друг от друга простых высказываний, которые связаны союзом «или».
Логическая форма: p или q, где p – «Всякий школьник не остроумен», q – «Некоторые школьники остроумны».
Выражение логически недетерминированное – не относится к числу логических законов.
Логическая форма с учетом внутренней структуры высказываний:
Всякий S не есть P или некоторый S есть P, где S – «Школьник», P – «Остроумный человек».
В такой интерпретации данное выражение является логическим законом, поскольку любое высказывание этой формы истинно.
-
Основные логические законы
Среди большого количества логических законов закон тождества, закон противоречия, закон исключенного третьего и закон достаточного основания считаются основными. Первые три закона были сформулированы еще Аристотелем, а четвертый – Лейбницем и до сих пор не утратили своей ценности.
Согласно закону тождества, всякое высказывание об одном и том же предмете в одно и то же время и в одном и том же отношении должно быть тождественно самому себе, сколько бы раз не воспроизводилось. Закон тождества может быть выражен формулой p→p.
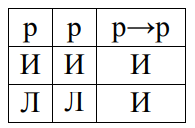
С законом тождества связано такое свойство логического мышления, как определенность. Несоблюдение требований закона тождества приводит к двусмысленности и неясности: «Она спрятала в карман записку от мужа». Часто мысль, высказанная вслух с некоторыми грамматическими ошибками, звучит абсурдно: «В деревне волки церковь съели». (Если же написать и произнести это выражение правильно, получится: «В деревне Волки церковь из ели».) Чаще всего нарушение требований закона тождества связано с синонимичностью и омонимичностью естественного языка и ассоциативностью человеческого мышления.
Закон противоречия гласит: два высказывания, находящиеся в отношении отрицания, не могут быть одновременно истинными, по крайней мере одно из них ложно. Для того чтобы закон противоречия действовал, надо рассуждать об одном и том же предмете, в одно и то же время в одном и том же отношении.
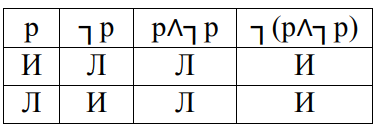
В законе противоречия зафиксировано такое свойство логического мышления, как непротиворечивость.
Подобно закону противоречия закон исключенного третьего выражает последовательность и непротиворечивость мышления. Закон противоречия касается всех несовместимых высказываний, в то время как закон исключенного третьего действует в отношении только противоречащих высказываний. Закон исключенного третьего: два противоречащих друг другу высказывания не могут быть ни одновременно истинными, ни одновременно ложными, одно из них истинно, другое – ложно, третьего не дано.
В соответствии с требованиями закона исключенного третьего только одна из альтернатив является истинной: «Число 7 либо четное, либо нечетное», «Студент Н. либо имеет водительское удостоверение, либо не имеет».
В XVIII в. Г. Лейбниц обратил внимание на такое свойство логического мышления, как обоснованность, и сформулировал закон достаточного основания: всякая истинная мысль должна быть обоснована. На символическом языке логики высказываний закон достаточного основания не записывается. Любая истинная мысль имеет основание в реальности. Поэтому мы можем найти и указать основания нашей мысли. Ложь же противоречит реальности. В сфере познавательной деятельности принимать истинность мысли на веру недопустимо. Достаточным основанием признания мысли истинной может быть личный опыт человека, непосредственное сопоставление некоторых мыслей с фактами действительности. Так же, опираясь на закрепленный в науке опыт человечества, мы можем логически обосновывать наши мысли, выводя их из уже установленных положений. Соблюдение закона достаточного основания делает наше мышление обоснованным и убедительным. Эти характеристики отличают научное мышление от ненаучного. Таким образом, достаточным основанием какой-либо мысли может быть любая другая, уже проверенная истинная мысль, из которой с необходимостью вытекает истинность данной мысли.
-
Понимание законов мышления в математической логике
Создателем современной символической логики следует считать Джорджа Буля. Буль для превращения логики в точную науку стал использовать математические обозначения. Он писал: «...необходимо связать логику не с философией, а с математикой» [3, с.68].
Буль строит алгебру высказываний (алгебру логики) как алгебру классов, в которой классы множеств соответствуют объёмам понятий. Буль обозначает универсальное множество символом 1, пустое множество символом 0, для обозначения классов использует переменные x, y, …. На множестве классов вводит двухместные операции x + y (сложение, соответствующее объединению множеств с исключением их общей части) и x * y (умножение, соответствующее пересечению множеств), одноместную операцию 1 - x (дополнение до универсума). В булевой алгебре для сложения и умножения выполняются коммутативный и ассоциативный законы, умножение дистрибутивно относительно сложения. Если использовать современные обозначения для дополнения, то следующие свойства операций в алгебре Буля можно записать в виде x * !x = 0, x + !x = 1. Буль отмечает, что логика отличается алгебры тем, что в логике выполняется равенство x * x = x тогда как в алгебре равенство x^2 = x выполняется только тогда, когда x = 1 или x = 0.
Традиционная логика Аристотеля имеет дело с понятиями, суждениями и умозаключениями. Суждения описывают простейшие взаимоотношения между понятиями. Четыре классических типа суждений:

В современной символике представляются так:

Формальная логика устанавливает ряд свойств суждений. Одно из таких свойств — отношение противоречия между суждениями типов A и O (а также между I и E): суждение типа A истинно тогда и только тогда, когда суждение типа O с теми же членами ложно. Например, 3 из истинности суждения «Все птицы — животные» вытекает ложность суждения «Некоторые птицы — не животные». Другим важнейшим разделом традиционной логики является учение о силлогизмах — элементарных умозаключениях, с помощью которых суждение с субъектом S и предикатом P (заключение силлогизма) выводится из двух других суждений (посылок силлогизма). Посылки силлогизма, помимо членов S и P, содержат еще один, средний член M. Пример:

Этот силлогизм построен по следующей схеме, содержащей три общеутвердительных суждения:
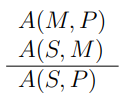
В современных обозначениях ему соответствует схема вывода:
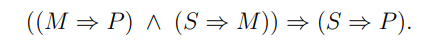
ЗАКЛЮЧЕНИЕ
Логический закон как ничто другое помогает разобраться в истинности или ложности того или иного явления. Четкая формулировка условий и следующий за ними закономерный вывод на основе анализа логических форм позволяет решать эту важную задачу. Основные логические законы являются прочным фундаментом, позволяющим решать сложные логические задачи и, соответственно, устанавливать истинность либо ложность события. Математизация законов мышления формализует и делает более лаконичными условия и вытекающие из них выводы, что способствует скорейшему решению различного рода задач.
Обобщая, можно сказать, что строгость и доказательность логических законов являются гарантом безошибочности и точности в следующих из вытекающих условий выводов.