ТИПОВОЕ ЗАДАНИЕ ПО ДИСЦИПЛИНЕ «ФИНАНСОВАЯ МАТЕМАТИКА» ДЛЯ ЗАОЧНИКОВ(задачи №№1-2 по теме «Ссудный и учетный процент»; задачи №№ 3-4 по теме «Различные способы начисления процентов. Простой и сложный процент»; задачи №№ 5-8 по теме «Финансовая рента», задачи№№9-10 – по теме «Способы начисления амортизации»)Вариант 8.Задача 1. X=30000; n=3; d=15. Задача 2. P= 80000; n=4; i= 20. Задача 3. Y=60000; n=5; ic=18. Задача 4. j1= 24; j2=18; j2=16. Задачи 5-8.  R = 50 тыс. руб. n = 10 лет. j = 10% Задачи 9-10. С = 1 млн. руб. Спи = 6 лет. Q1= 50 тыс.ед. Q2= 70 тыс.ед. Q3= 90 тыс.ед. Q4= 100 тыс.ед. Q5=140тыс.ед.  Q6 = 150 тыс.ед.

1. 
   Задача 1. Вексель номиналом X рублей учтен в банке за n месяцев до погашения. Определите сумму, полученную владельцем векселя, если ставка учетного процента равен d (% годовых).
   

Решение:x (номинал векселя)=30000 руб.; n(период до погашения)=3 мес.; d(ставка учетного процента)=15%. Определим сумму, полученную по векселю по формуле простого процента:S=P (1+nd) или при неполном сроке лет:S= P* (1+ 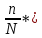d) где: S = будущая сумма,P = номинал векселя (первоначальная сумма),n = срок оплаты;d процентная ставка,n = срок оплаты – 3 месяца = 90 днейN – количество дней в году = 365Сумма, полученная по векселю составит:S = 30000 (1+ 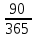* 0,15) = 31109,6 руб.Ответ: Владелец векселя получит сумму в размере 31109,6 руб.

2. 
   Задача 2. Покупатель приобретает в магазине товар по цене P рублей. На всю сумму он берет кредит, который должен быть возвращен в течение n лет. Определите всю сумму долга, при условии, что ставка простого ссудного процента равна i (% годовых).
   

Решение:P (сумма кредита – первоначальная сумма)= 80000 руб.; N (срок кредита)=4 года; I (процент по кредиту)= 20%Сумму долга определяем по формуле простого процента:S=P (1+nd) где: S = сумма долга – будущая сумма,

---

P = сумма кредита – первоначальная сумма,n = срок кредита;d ставка ссудного процента.S=80000*(1+0,2*4) = 144000 руб.Ответ: Сумма долга составит 144000 руб.

3. 
   Задача 3. Какой величины достигнет размер долга, равный Y руб., через n лет при росте по сложной процентной ставке i_с (% годовых)?
   

Решение:Y (размер долга - первоначальный)=60000 руб.; n (период)=5 лет; i_c (процентная ставка сложная)=18%Сумму будущего долга определяем по формуле сложного процента:S=Y (1+i_c)ⁿ где: S = сумма будущего долга,Y = сумма кредита – первоначальная сумма,n = срок кредита;i_c сложная процентная ставка.S=60000 (1+0,18)⁵ = 137265,5 руб.Ответ: Сумма будущего долга составит 137265,5 руб. 

4. 
   Задача 4. Рассчитайте эффективные процентные ставки по депозитным договорам и определите наиболее выгодный процент для вкладчика:
   

а) годовой процент j₁(%), периодичность начисления один раз в полгода;б) годовой процент j₂(%, периодичность начисления один раз в квартал;в) годовой процент j₃(%), периодичность начисления один раз в год.Решение:j1(годовой процент с периодичностью 1 раз в полгода)= 24%; j2(годовой процент с периодичностью 1 раз в квартал)=18%; j3(годовой процент с периодичностью 1 раз в год)=16%.Годовую эффективную ставку процента определим по формуле:iэ = 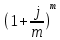– 1где: iэ – эффективная годовая процентная ставка;m – количество начислений в году;j 1,2,3– годовой процент (номинальная процентная ставка).i_э1=(1+ 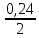)² – 1= 0,2544 = 25,44%;i_э2=(1+ 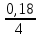)⁴ – 1= 0,1925 = 19,25%;i_э3=(1+ 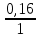)¹ – 1= 0,16= 16%;Ответ: Эффективная процентная ставка i_э1=25,44%, i_э2=19,25%, i_э3=16%. Эффективная ставка процента

---

показывает реальный доход инвестора от вклада или эффективность роста денег на счету вкладчика, следовательно наиболее выгодным процентом будет являться i_э1=25,44%

5. 
   Задача 5. На счет в банке в течение n лет ежегодно (в начале каждого года) вносится сумма в размере R руб., на которую в конце года 1 раз в год начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада).
   

Решение:R (вносимая в банк сумма)= 50 тыс. руб. n = (период вложения средств)= 10 летj (номинальная процентная ставка) =10% Так как период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. 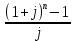конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента.Сумма всех взносов с начисленными процентами будет равна:FVA = R где: FVA – наращенная сумма – сумма всех взносов с начисленными процентами;R – вносимая в банк сумма;j – номинальная процентная ставка;n – период вложения средств.FVA = 50000 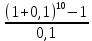= 796871,2 руб.Сумма взносов в течение 10 лет составит:P = n * RP =10 * 50000 = 500000 руб.Сумма начисленных процентов будет равна:I = FVA – PI = 796871,2 – 500000 = 296871,2 руб.Ответ: Доход владельца счета за весь срок ренты составит 296871,2 руб.

5. 
   Задача 6. На счет в банке в течение n лет ежегодно (в начале каждого года) вносится сумма в размере R руб, на которую ежеквартально (в конце каждого квартала) начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада).
   

---

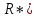
Решение:R (вносимая в банк сумма)= 50 тыс. руб. n = (период вложения средств)= 10 летj (номинальная процентная ставка) =10% Взносы начисляются в начале периода ренты, значит аннуитет пренумерандо Рассчитать будущую стоимость аннуитета пренумерандо можно воспользовавшись следующей формулой.FVA = 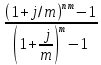* (1+j/m) где: FVA – наращенная сумма – сумма всех взносов с начисленными процентами;R – вносимая в банк сумма;j – номинальная процентная ставка;n – период вложения средств.FVA = 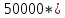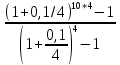* (1+0,1/4) = 50000* 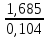*1,025 = 831876,7 руб.Сумма взносов в течение 10 лет составит:P = n * RP =10 * 50000 = 500000 руб.Сумма начисленных процентов будет равна:I = FVA – PI = 831876,7 – 500000 = 331876,7 руб.Ответ: Доход владельца счета за весь срок ренты составит 331876,7 руб.

5. 
   Задача 7. На счет в банке в течение n лет ежегодно вносится сумма в размере R руб, но взносы поступают ежеквартально, равными частями (т.е. R/4). На размер годовых поступлений R ежеквартально начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада).
   

Решение:

5. 
   Задача 8. На счет в банке в течение n лет ежегодно вносится сумма в размере R руб, но взносы поступают ежеквартально, равными частями (т.е. R/4). На размер годовых поступлений R ежемесячно начисляются проценты по номинальной ставке j процентов годовых. Определить доход владельца счета за весь срок ренты (т.е. сумму начисленных процентов, которую банк должен выплатить владельцу счета по истечении срока вклада)
   

FVA =

5. 
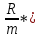
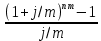
   Задача 9. Определить годовую норму амортизации и годовую сумму амортизационных отчислений для каждого года срока полезного использования основных средств, используя способ списания стоимости по сумме числе лет срока полезного использования, если известна первоначальная стоимость объекта основных средств С и срок его полезного использования C_пи.
   

---

Решение:С (первоначальная стоимость основных средств) = 1 млн. руб. С_пи (срок полезного использования) = 6 лет. Q1(объем продукции)= 50 тыс.ед. Q2(объем продукции)= 70 тыс.ед. Q3(объем продукции)= 90 тыс.ед. Q4(объем продукции)= 100 тыс.ед. Q5(объем продукции)=140 тыс.ед.  Q6 (объем продукции)= 150 тыс.ед.Норма амортизации – это установленный в процентах от стоимости размер амортизации за определенный период времени по конкретному виду основных фондов. 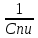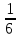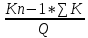Рассчитывается по формуле:Na = *100где: Na – норма амортизационных отчислений;С_пи – срок полезного использования.Na = *100 = 16,66%Сумму амортизации за каждый год использования основного средства по способу списания стоимости по сумме числе лет срока полезного использования рассчитывается по формуле: Аi = где: Аi – годовая сумма амортизационных отчислений для каждого года;K_n-1 – количество лет, оставшихся до конца срока полезного использования основного средства;∑K – сумма чисел лет срока полезного использования, ед.С – первоначальная сумма основных средств.Сумма чисел лет срока полезного использования основных средств равна:1 + 2 + 3 + 4 + 5 + 6= 21 год.В первый год эксплуатации основных средств годовая сумма амортизации составит:6: 21 × 1000000 руб. = 285714,3 руб.Во второй год эксплуатации основных средств годовая сумма амортизации составит:5 : 21 × 1000000 руб. = 238095,2 руб.В третий год эксплуатации основных средств сумма амортизации составит:4: 21 × 1000000 руб. = 190476,2 руб.В четвертый год эксплуатации основных средств сумма амортизации составит:3: 21 × 1000000 руб. = 142857,1 руб.В пятый год эксплуатации основных средств сумма амортизации составит:2: 21 × 1000000 руб. = 95238,1 руб.В шестой год эксплуатации основных средств сумма амортизации составит:

---

Смотрите также файлы

• Для практической работы.docx

• Правописание частицы не с глаголами.docx

• Провести анализ эффективности использования основных средств организации. Провести факторный анализ влияния изменения среднегодовой стоимость основных средств и фондоотдачи на изменение выручки организации.docx

• Методические указания по подготовке курсовой работы по дисциплине с 13 Гражданское право.docx

• Международного и промышленного менеджмента и коммуникации.docx