1. 
   Гармонические колебания. Собственные колебания механических систем. Уравнение колебаний. Дифференциальное уравнение. Энергия колебаний.
   

Гармонические колебания – колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.



Собственные колебания – колебания, происходящие под воздействием внутренней возвращающей силы. Например, в случае математического маятника это сила тяжести, а в случае пружинного маятника – сила упругости.

Дифференциальное уравнение, описывающее гармоническое колебание:



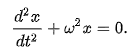
При гармонических колебаниях происходит превращение потенциальной энергии в кинетическую и обратно, при этом полная энергия системы остается неизменной.

2. 
   Математический, пружинный и физический маятник.
   

Математи́ческий ма́ятник представляет собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения. При этом другой конец нити или стержня неподвижен.





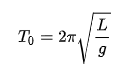
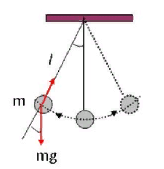
Пружинный маятник представляет собой груз, прикрепленный к пружине, массой которой можно пренебречь. В пружинном маятнике колебания совершаются под действием силы упругости. Пока пружина не деформирована, сила упругости на тело не действует.




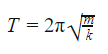
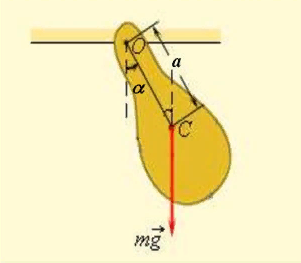
Физический маятник представляет собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

---

3. 
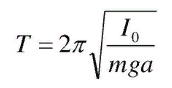
   Затухающие колебания – характеристики. Вынужденные колебания. Резонанс (уравнения, рисунки)
   

Затухающие колебания характеризуются коэффициентом затухания:



Логарифмический декремент затухания:



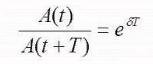
Добротность – отношение энергии систем в момент времени t к убыли этой энергии за один последующий период затухающих колебаний.



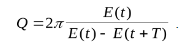
Вынужденные колебания – колебания, происходящие под воздействием внешней периодической силы на данную системы.

Резонанс – явление резкого возрастания амплитуды колебаний, в следствие совпадения частоты и фазы внешней периодической силы с частотой и фазой собственных колебаний.



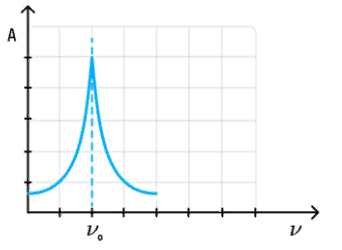
Явление резонанса может нести как пользу, так и вред: из-за него происходит обрушение зданий и сооружений, но он же является основой, главным фактором в работе музыкальных инструментов.

4. 
   Виды волн. Дифференциальное волновое уравнение. Уравнение плоской волны. Длина волны, волновое число, фазовая скорость
   

Волны бывают продольными и поперечными. Если колебания возмущенной величины происходят перпендикулярно направлению распространения волны, то волна называется поперечной, а если параллельно, то продольной. Так, поплавок на воде колеблется вверх-вниз, а волна распространяется в горизонтальном направлении и потому является поперечной.

Дифференциальное волновое уравнение:

---

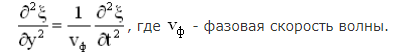
Уравнение плоской волны:



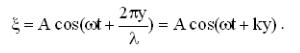
Длиной волны   называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна  ).

Фазовая скорость   - это скорость распространения данной фазы колебаний, т.е. скорость волны.

Связь длины волны  , фазовой скорости   и периода колебаний Т задается соотношением:

.

Волново́е число́ — это отношение 2π радиан к длине волны:

5. 
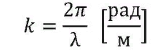
   Электромагнитные волны. Вектора, характеризующие электромагнитную волну- уравнения. Шкала электромагнитных волн.
   

Взаимное образование электрических и магнитных полей приводит к понятию электромагнитной волны — распространение единого электромагнитного поля в пространстве.

Так как электромагнитная волна образована электрическим и магнитным полем, то и описывается она с помощью векторов напряженности и магнитной инудукции.



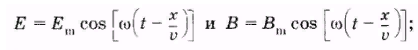
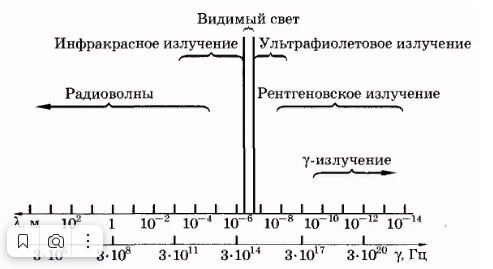
Шкала электромагнитных волн.

Вся шкала условно подразделена на шесть диапазонов: радиоволны (длинные, средние и короткие), инфракрасные, видимые, ультрафиолетовые, рентгеновские волны и гамма-излучение.

6. 
   Световые волны. Когерентные источники. Интерференция света
   

Световые волны – группа электромагнитных волн, у которых длина волны находится в диапазоне примерно от 380 нм до 780 нм.

---

Интерференцией света называется наложение когерентных световых волн, в результате которого происходит перераспределение световой энергии в пространстве, и в одних точках пространства наблюдается усиление световых колебаний, а в других – ослабление. Когерентными называются волны, имеющие одинаковую частоту и постоянную во времени разность фаз колебаний. Никакие два светящихся тела, кроме лазеров, не могут являться источниками когерентных световых волн. Свет от светящегося тела представляет собой совокупность множества электромагнитных волн, которые излучаются отдельными атомами и молекулами нагретого тела. Для получения двух когерентных источников света на практике используют щели Юнга, таким образом из одного источника света получают два источника две щели, от которых идет один и тот же свет).

При рассмотрении интерференции света важно понимать разность пройденных волнами расстояний – разность хода. При интерференции образуются чередующиеся светлые и темные пятна.

Условие максимума(светлые пятна):



Условие минимума(темные пятна):

7. 
   Дифракция Фраунгофера на щели и на дифракционной решетке. Дифракционные спектры. Условие возникновение максимумов дифракционной картины. Чем отличаются дифракционные картины при дифракции на щели и дифракционной решетке.
   

Дифракция Фраунгофера на одиночной щели. Параллельный пучок монохроматического света падает нормально на непрозрачную преграду, (рисунок 6.4.1), в котором прорезана узкая щель ВС, имеющая постоянную ширину   и длину   . Условие   позволяет рассматривать эту щель, как узкую щель бесконечной длины. В соответствии с принципом Гюйгенса – Френеля точки щели являются вторичными источниками волн, колеблющимися в одной фазе, так как плоскость щели совпадает с фронтом падающей волны. 

---

Дифракция Фраунгофера на дифракционной решетке. Дифракционной решеткой называется совокупность большого числа узких одинаковых, отстоящих друг от друга на одно и то же расстояние, щелей (рисунок 6.4.2). Расстояние d между серединами соседних щелей называется периодом решетки. Период решетки равен сумме ширины щели а и расстояния между щелями b, т.е.   . Решетка также характеризуется числом штрихов на единицу длины  , где N – полное число штрихов в решетке,  – длина решетки.

Дифракционная картина представляет собой систему светлых пятен, расположенных в определенном порядке на плоскости экрана. Размеры этих пятен уменьшаются при увеличении числа щелей, а яркость возрастает. Такая же картина получается, если на одно стекло нанести ряд взаимно перпендикулярных полос. За счет большего количества лучей дифракционная картина получается более выраженной(пятна ярче, границы более чёткие)

Дифракционный спектр:

8. 
   Поляризованный свет. Законы Малюса и Брюстера
   

Поляризация света — выделение из пучка естественного света лучей, поляризованных в определенной плоскости.

Поляризованный свет — свет, в котором колебания вектора подчинены определенному закону.

Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла ϕ между плоскостями поляризации падающего света и поляризатора.



Закон Брюстера — закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом преломлённый луч частично поляризуется в плоскости падения, и его поляризация достигает наибольшего значения. Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера. При падении под углом Брюстера отражённый и преломлённый лучи взаимно перпендикулярны.

---

Смотрите также файлы

• Дополнительное образование настоящее и будущее.docx

• Министерство образования Красноярского края краевое государственное бюджетное.docx

• Понятие обязательства вследствие причинения вреда и условия его возникновения.docx

• Выполнение практических заданий по дисциплине макроэкономика.docx

• Календарнотематическое планирование составлено.doc