Файл: По данным лабораторных испытаний необходимо построить график компрессионной зависимости вида.docx
Добавлен: 06.12.2023
Просмотров: 13
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Архитектурно-строительный институт
(наименование института полностью)
Кафедра /департамент /центр Центр архитектурных, конструктивных решений и
организации строительства
(наименование кафедры/департамента/центра полностью)
08.03.01 Строительство
(код и наименование направления подготовки, специальности)
Промышленное и гражданское строительство
(направленность (профиль) / специализация)
Практическое задание № 2
по учебному курсу «Механика Грунтов»
(наименование учебного курса)
Вариант 10
| Студент | (И.О. Фамилия) | |
| Группа | (И.О. Фамилия) | |
| Преподаватель | Е. А. Ушакова (И.О. Фамилия) | |
Тольятти 2022
Задача 2.1.
Исходные данные.
По данным лабораторных испытаний необходимо построить график компрессионной зависимости вида
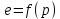. Вычислите для заданного расчетного интервала давлений коэффициент относительной сжимаемости mν и модуль деформации E. Дайте оценку степени сжимаемости грунта. Определите разновидность грунтов по деформируемости. Начальная высота образца грунта h = 20 мм.Разновидность грунта – суглинок с коэффициентом пористости e = 0,6 д.е.
| № вар. | Полная осадка грунта Si , мм при нагрузке Pi, Мпа | Интервал давлений, МПа | ||||||
| | 0,05 | 0,1 | 0,2 | 0,3 | 0,5 | P1 | P2 | |
| 10 | 0,05 | 0,27 | 0,42 | 0,55 | 0,81 | 0,1 | 0,5 | |
Построение компрессионной кривой
Для построения компрессионной кривой и определения коэффициента относительной сжимаемости грунта mν необходимо вычислить коэффициенты пористости грунта ei, соответствующие заданным ступеням нагрузки, по формуле:
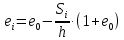, (2.1)где
ei – искомое значение коэффициента пористости грунта после уплотнения под нагрузкой;
e0 – начальное значение коэффициента пористости грунта после уплотнения под нагрузкой;
Si– полная осадка образца грунта при заданной нагрузке, измеренная от начала загружения;
h – начальная высота образца грунта.
Коэффициенты пористости при соответствующих давлениях:
,
,
,
,
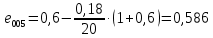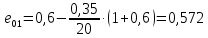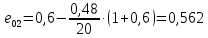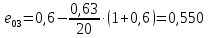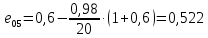.По полученным данным строится компрессионная кривая, показанная на рисунке 2.1.
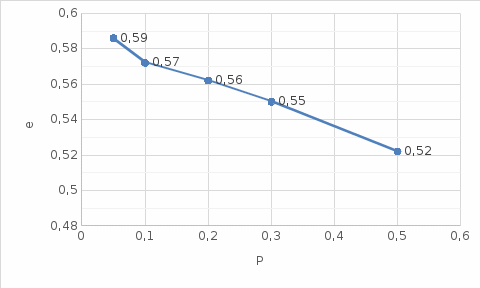
Рисунок 2.1 – График компрессионной зависимости.
В пределах давлений, указанных в задании, определяется коэффициент сжимаемости грунта:
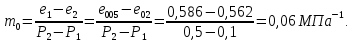(2.2)Коэффициент относительной сжимаемости определяется по формуле:
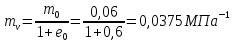. (2.3)Модуль деформации грунта определяется по формуле:
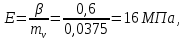(2.4)где
β – коэффициент, учитывающий отсутствие поперечного расширения грунта в приборе и назначаемый в зависимости от коэффициента Пуассона ν, определяемый по формуле:
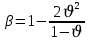. (2.5)При отсутствии экспериментальных данных допускается принимать β, равным для песков – 0,8; супесей – 0,7; суглинков – 0,6; глин – 0,4.
Вывод: по таблице Б.1 приложения Б определяется разновидность грунта по деформируемости – грунт является среднедеформируемым.
Задача 2.2.
Исходные данные.
По полученным экспериментальным данным определите нормативное значение угла внутреннего трения φн и сцепление снгрунта. Постройте график сдвига вида
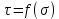.| № вар | Предельное сопротивление образца грунта сдвигу τi, МПа, при нормальном давлении, передаваемом на образец грунта σi, МПа | |||||
| | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
| 10 | 0,12 | 0,16 | 0,196 | 0,235 | 0,27 | 0,308 |
Решение.
По полученным экспериментальным данным необходимо построить график сдвига вида
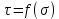, как показано на рисунке 2.2.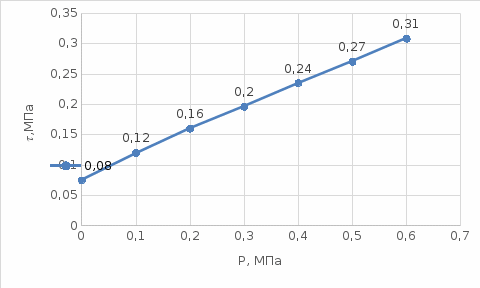
Рисунок 2.2 - График сдвига вида
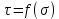.Для определения нормативного значения угла внутреннего трения грунта и сцепления грунта следует воспользоваться формулами, составленными на основе законов математической статистики:
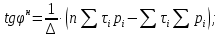(2.6)
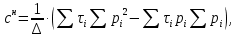(2.7)где
n – число экспериментов по определению сопротивления грунта сдвигу (n = 6);
Δ – общий знаменатель этих выражений, определяемый по формуле:
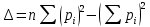. (2.8)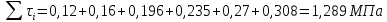
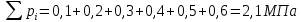
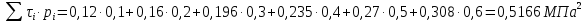
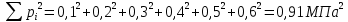
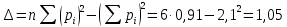
Нормативное значение сцепления грунта:
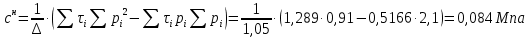.Нормативное значение тангенса угла внутреннего трения грунта:
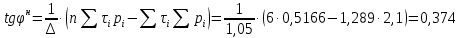.Нормативное значение угла внутреннего трения грунта: φ = 20,5º.
Задача 2.3.
Исходные данные.
Поверхность грунтового потока имеет угол уклона α. Коэффициент фильтрации грунта Кф. Необходимо определить ориентировочное время заполнения водой траншеи заданной ширины, которая пересекает грунтовый поток и заглублена ниже уровня грунтовых вод.
| № вар | Угол наклона α, град | Коэффициент фильтрации, Кф, м/сут | Ширина траншеи L, м |
| 10 | 33 | 50 | 2,5 |
Решение
Необходимо определить градиент гидравлического напора:
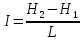(2.9)Как видно из рисунка 2.3, гидравлический градиент напора будет равен:
.
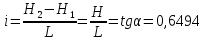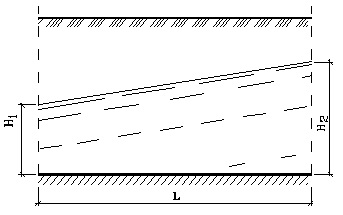
Рисунок 2.3 – Определение градиента гидравлического напора
Скорость фильтрации определяется по формуле:
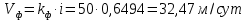. (2.10)Скорость фильтрации Vф – это расход поровой воды через единицу поперечного сечения в единицу времени.
Тогда грунтовый поток пройдет путь, равный ширине траншеи, за время:
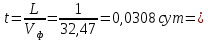0,7392 часа =44,352 мин. (2.11)Полученное время можно считать временем (ориентировочным) заполнения траншеи водой.
Приложение Б
Таблица Б.1 – Разновидности грунтов по деформируемости (ГОСТ 25100-2011)
| Разновидность грунтов | Модуль деформации Е, МПа |
| Очень сильно деформируемые | Е ≤ 5 |
| Сильнодеформируемые | 5 < E ≤ 10 |
| Среднедеформируемые | 10 < E ≤ 50 |
| Слабодеформируемые | E > 50 |