Файл: исследование квадратичной функции с помощью паскаль.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- Закрашивает один пиксел с координатами (x,y) цветом color LineTo(x,y) - рисует отрезок от текущего положения пера до точки (x,y); координаты пера при этом также становятся равными (x,y).
Line(x1,y1,x2,y2) - рисует отрезок с началом в точке (x1,y1) и концом в точке (x2,y2).
SetPenColor(color) - устанавливает цвет пера, задаваемый параметром color.
SetPenWidth(n) - устанавливает ширину (толщину) пера, равную n пикселям.
Rectangle(x1,y1,x2,y2) - рисует прямоугольник, заданный координатами противоположных вершин (x1,y1) и (x2,y2).
FloodFill(x,y,color) - заливает область одного цвета цветом color, начиная с точки (x,y).
SetBrushColor(color) - устанавливает цвет кисти. Заливка кистью распространяется на замкнутый контур, описание которого следует за процедурой установки цвета кисти.
Ellipse(x1,y1,x2,y2) - рисует эллипс, заданный своим описанным прямоугольником с координатами противоположных вершин (x1,y1) и (x2,y2).
Circle(x,y,r) - рисует окружность с центром в точке (x,y) и радиусом r.
Arc(x,y,r,a1,a2) - Рисует дугу окружности с центром в точке (x,y) и радиусом r, заключенной между двумя лучами, образующими углы a1 и a2 с осью OX (a1 и a2 – вещественные, задаются в градусах и отсчитываются против часовой стрелки).
2.1. Теоретическая часть
Функция вида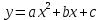
, где a≠0
называется квадратичной функцией.
В уравнении квадратичной функции:
a - старший коэффициент
b - второй коэффициент
с - свободный член.
Графиком квадратичной функции является квадратичная парабола.
Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции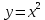
при любых значениях остальных коэффициентов.
Если старший коэффициент a >0, то ветви параболы направлены вверх.
Если старший коэффициент a <0, то ветви параболы направлены вниз.
Второй параметр для построения графика функции - значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) – это точки пересечения графика функции y=f(x) с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю
, чтобы найти координаты точек пересечения графика функции y=f(x) с осью ОХ, нужно решить уравнение f(x)=0.
В случае квадратичной функции
нужно решить квадратное уравнение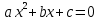 
.
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: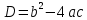
, который определяет число корней квадратного уравнения.
И здесь возможны три случая:
, 
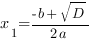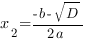
Следующий важный параметр графика квадратичной функции - координаты вершины параболы:
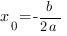
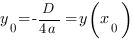
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции - точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c.
То есть точка пересечения параболы с осью OY имеет координаты (0;c).[2]
2.2. Практическая часть
Исследование № 1
Цель: с помощью программы в Pascal проанализировать изменение графика функции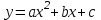
от коэффициента a.
Ход работы:
1. Построить графики функции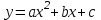 с разными коэффициентами a.
2. Сравнить результаты и сделать вывод.
Вывод: 1) Знак коэффициента
отвечает за направление ветвей. При а>0 ветви направлены вверх, при а <0 — вниз.
2) Абсолютная величина коэффициента (модуля) отвечает за “расширение”, “сжатие” параболы. Если |a|>1, тем уже парабола, |a| <0, тем шире парабола.
Исследование № 2
Цель: с помощью программы в Pascal проанализировать изменения графика функции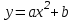
от коэффициента b.
Ход работы:
1. Построить графики функции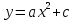
с разными коэффициентами c.
2. Сравнить результаты и сделать вывод.
Вывод: если c>0, то график функции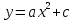
смещается по оси Оу вверх на c единиц, если c<0, график смещается вниз на c единиц.
Исследование № 3
Цель: решить квадратное уравнение.
Ход работы:
Пример 1. Решить уравнение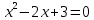
Пример 2. Решить уравнение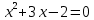
Пример 3. Решить уравнение
Решить уравнение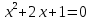
Заключение
Мы познакомились с языком программирования Паскаль, узнав его историю, к примеру, мы узнали, что этому языку уже более 50 лет. Далее разобрались с его особенностями, а также с языковыми конструкциями. Следующим этапом, приступили к разработке программы. Для этого мы тщательно изучили вопрос о решении уравнений через Дискриминант, изучили формулы и последовательность решения. Используя базовые команды смогли написать рабочую программу. Данный проектный продукт можно использовать для того, чтобы построить график функции, проверить, правильные ли получились корни в ответе.
Список литературы
Приложение 1
program proekt;
uses graphABC;
var b,c,gx,gy,x0,k,y0,x1,y1,i:integer;
x,y,D,x11,x22,a:real;
begin
writeln( 'Введите коэффициенты уравнения');
readln (a,b,c);
if a>0 then writeln ('Ветви параболы направлены вверх') else writeln ('Ветви параболы направлены вниз');
if c>0 then writeln ('График функции сместится по оси оу вверх на ' , c ) else writeln ('График функции сместится по оси оу вниз на ' , c );
gx:=1000;
gy:=1300;
k:=10; //масштаб
setwindowsize (gx,gy);
x0:=gx div 2; //центр Х
y0:=gy div 2; //центр Y
///ось х
line(0,y0,gx,y0);
line(gx,y0,gx-10,y0+10);
line(gx,y0,gx-10,y0-10);
textout(gx-10,y0+10,'X');
/// ось y
line(x0,0,x0,gy);
line(x0,0,x0-10,10);
line(x0,0,x0+10,10);
textout(x0+10,10,'Y');
///цикл для цены деления X
i:=-20;
while i<21 do
begin
line(x0+i*k,y0+5,x0+i*k,y0-5);
textout(x0+i*k,y0+10,inttostr(i));
i:=i+2;
end;
///цикл для цены деления Y
i:=-20;
while i<21 do
begin
if i<>0 then
begin
line(x0+5,y0+i*k,x0-5,y0+i*k);
textout(x0+10,y0-i*k,inttostr(i));
end;
i:=i+2;
end;
x:=-5;
while x<=5 do
begin
y:=a*x*x+b*x+c;
x1:=x0+ round(x*k); //коорд Х относительно центра
y1:=y0- round(y*k); //коорд Y относительно центра
setpencolor(clred);
circle(x1,y1,2);
floodfill(x1,y1,clred);
x:=x+0.1;
end;
D := sqr(b) - 4 * a * c;
if D < 0 then
writeln('Квадратное уравнение не имеет корней')
else
begin
if D = 0 then
begin
{квадратное уравнение имеет два одинаковых корня}
x11 := -b / (2 * a);
x22 := x11;
end
else
begin
{уравнение имеет два разных корня}
x11 := (-b + sqrt(D)) / (2 * a);
x22 := (-b - sqrt(D)) / (2 * a);
end;
{вывод корней уравнения}
writeln('x1 = ', x11:8:3);
writeln('x2 = ', x22:8:3);
end;
end.21>21>0>
Line(x1,y1,x2,y2) - рисует отрезок с началом в точке (x1,y1) и концом в точке (x2,y2).
SetPenColor(color) - устанавливает цвет пера, задаваемый параметром color.
SetPenWidth(n) - устанавливает ширину (толщину) пера, равную n пикселям.
Rectangle(x1,y1,x2,y2) - рисует прямоугольник, заданный координатами противоположных вершин (x1,y1) и (x2,y2).
FloodFill(x,y,color) - заливает область одного цвета цветом color, начиная с точки (x,y).
SetBrushColor(color) - устанавливает цвет кисти. Заливка кистью распространяется на замкнутый контур, описание которого следует за процедурой установки цвета кисти.
Ellipse(x1,y1,x2,y2) - рисует эллипс, заданный своим описанным прямоугольником с координатами противоположных вершин (x1,y1) и (x2,y2).
Circle(x,y,r) - рисует окружность с центром в точке (x,y) и радиусом r.
Arc(x,y,r,a1,a2) - Рисует дугу окружности с центром в точке (x,y) и радиусом r, заключенной между двумя лучами, образующими углы a1 и a2 с осью OX (a1 и a2 – вещественные, задаются в градусах и отсчитываются против часовой стрелки).
2.1. Теоретическая часть
Функция вида
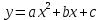, где a≠0 называется квадратичной функцией.В уравнении квадратичной функции:
a - старший коэффициент
b - второй коэффициент
с - свободный член.
Графиком квадратичной функции является квадратичная парабола.
Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции
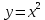при любых значениях остальных коэффициентов.Если старший коэффициент a >0, то ветви параболы направлены вверх.
Если старший коэффициент a <0, то ветви параболы направлены вниз.
Второй параметр для построения графика функции - значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) – это точки пересечения графика функции y=f(x) с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю
, чтобы найти координаты точек пересечения графика функции y=f(x) с осью ОХ, нужно решить уравнение f(x)=0.
В случае квадратичной функции
нужно решить квадратное уравнение 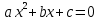.Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант:
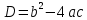, который определяет число корней квадратного уравнения.И здесь возможны три случая:
-
Если D<0
,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. -
Если D=0 ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. -
Если D>0 ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
, Следующий важный параметр графика квадратичной функции - координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции - точка пересечения параболы
с осью OY.Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы
с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c.То есть точка пересечения параболы с осью OY имеет координаты (0;c).[2]
2.2. Практическая часть
Исследование № 1
Цель: с помощью программы в Pascal проанализировать изменение графика функции
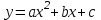от коэффициента a.Ход работы:
1. Построить графики функции
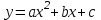с разными коэффициентами a.2. Сравнить результаты и сделать вывод.
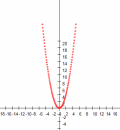
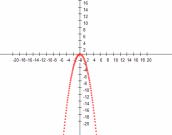
| a=1, b=0, c=0 | a=-1, b=0, c=0 |
 |  |
| a=2, b=0, c=0 | a=0.25, b=0, c=0 |
 |  |
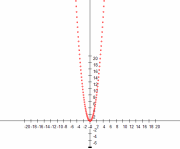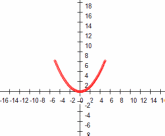Вывод: 1) Знак коэффициента
отвечает за направление ветвей. При а>0 ветви направлены вверх, при а <0 — вниз. 2) Абсолютная величина коэффициента (модуля) отвечает за “расширение”, “сжатие” параболы. Если |a|>1, тем уже парабола, |a| <0, тем шире парабола.
Исследование № 2
Цель: с помощью программы в Pascal проанализировать изменения графика функции
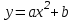от коэффициента b.Ход работы:
1. Построить графики функции
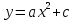с разными коэффициентами c.2. Сравнить результаты и сделать вывод.
| a=1, b=0, c=3 | a=1, b=0, c=-2 |
 |  |
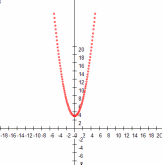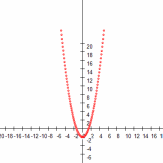Вывод: если c>0, то график функции
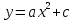смещается по оси Оу вверх на c единиц, если c<0, график смещается вниз на c единиц.Исследование № 3
Цель: решить квадратное уравнение.
Ход работы:
-
С помощью программы в Pascal решить квадратное уравнение. -
Решить уравнение, используя формулы корней квадратных уравнений. -
Сравнить результаты и сделать вывод.
Пример 1. Решить уравнение
-
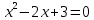
Построим график функции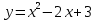
. -
Данное уравнение не имеет корней, так как дискриминант <0.
| График функции 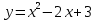| Выводы |
 |  |
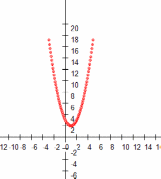Пример 2. Решить уравнение
-
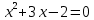
Построим график функции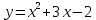
. -
Уравнение имеет 2 разных корня, так как дискриминант >0.
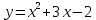| | Выводы |
 |  |
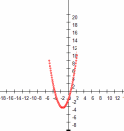Пример 3. Решить уравнение
Решить уравнение
-
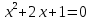
Построим график функции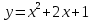
. -
Уравнение имеет 2 одинаковых корня, так как дискриминант = 0.
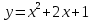| | Выводы |
 |  |
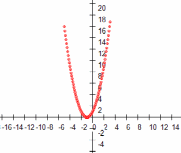Заключение
Мы познакомились с языком программирования Паскаль, узнав его историю, к примеру, мы узнали, что этому языку уже более 50 лет. Далее разобрались с его особенностями, а также с языковыми конструкциями. Следующим этапом, приступили к разработке программы. Для этого мы тщательно изучили вопрос о решении уравнений через Дискриминант, изучили формулы и последовательность решения. Используя базовые команды смогли написать рабочую программу. Данный проектный продукт можно использовать для того, чтобы построить график функции, проверить, правильные ли получились корни в ответе.
Список литературы
-
Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г.Мордкович. - 12-е изд., стер. - М.: Мнемозина, 2010. - 215 с. -
Симонович С.В. Информатика: Базовый курс / С.В.Симонович и др. - СПб.: Питер, 2001. - 640с. -
Семакин И.Г. Основы программирования: Учебник для сред. проф. образования / И.Г.Семакин, А.П.Шестаков. – 2-е изд., стер. – М.: Издательский центр «Академия», 2003. -
https://ru.wikipedia.org/wiki/Паскаль_(язык_программирования)
Приложение 1
program proekt;
uses graphABC;
var b,c,gx,gy,x0,k,y0,x1,y1,i:integer;
x,y,D,x11,x22,a:real;
begin
writeln( 'Введите коэффициенты уравнения');
readln (a,b,c);
if a>0 then writeln ('Ветви параболы направлены вверх') else writeln ('Ветви параболы направлены вниз');
if c>0 then writeln ('График функции сместится по оси оу вверх на ' , c ) else writeln ('График функции сместится по оси оу вниз на ' , c );
gx:=1000;
gy:=1300;
k:=10; //масштаб
setwindowsize (gx,gy);
x0:=gx div 2; //центр Х
y0:=gy div 2; //центр Y
///ось х
line(0,y0,gx,y0);
line(gx,y0,gx-10,y0+10);
line(gx,y0,gx-10,y0-10);
textout(gx-10,y0+10,'X');
/// ось y
line(x0,0,x0,gy);
line(x0,0,x0-10,10);
line(x0,0,x0+10,10);
textout(x0+10,10,'Y');
///цикл для цены деления X
i:=-20;
while i<21 do
begin
line(x0+i*k,y0+5,x0+i*k,y0-5);
textout(x0+i*k,y0+10,inttostr(i));
i:=i+2;
end;
///цикл для цены деления Y
i:=-20;
while i<21 do
begin
if i<>0 then
begin
line(x0+5,y0+i*k,x0-5,y0+i*k);
textout(x0+10,y0-i*k,inttostr(i));
end;
i:=i+2;
end;
x:=-5;
while x<=5 do
begin
y:=a*x*x+b*x+c;
x1:=x0+ round(x*k); //коорд Х относительно центра
y1:=y0- round(y*k); //коорд Y относительно центра
setpencolor(clred);
circle(x1,y1,2);
floodfill(x1,y1,clred);
x:=x+0.1;
end;
D := sqr(b) - 4 * a * c;
if D < 0 then
writeln('Квадратное уравнение не имеет корней')
else
begin
if D = 0 then
begin
{квадратное уравнение имеет два одинаковых корня}
x11 := -b / (2 * a);
x22 := x11;
end
else
begin
{уравнение имеет два разных корня}
x11 := (-b + sqrt(D)) / (2 * a);
x22 := (-b - sqrt(D)) / (2 * a);
end;
{вывод корней уравнения}
writeln('x1 = ', x11:8:3);
writeln('x2 = ', x22:8:3);
end;
end.21>21>0>