Файл: Лабораторная работа 2 Упругие и неупругие удары по курсу Физика 1 Тема Законы сохранения Цель работы Выбрать физические модели для анализа взаимодействия двух тел.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 22
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 2 «Упругие и неупругие удары»
по курсу «Физика 1»
Тема 3. Законы сохранения
Цель работы:
-
Выбрать физические модели для анализа взаимодействия двух тел. -
Исследовать физические характеристики, сохраняюшиеся при столкновениях. -
Экспериментальное определение зависимости тепловыделения при неупругом столкновении от соотношения масс при разных скоростях.
-
Зарисовка модели «Упругие и неупругие соударения»:

Эксперимент 1. Абсолютно упругий удар
-
Проведем измерения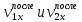 для абсолютно упругого удара тележек и запишем данные в таблицу 2.
для абсолютно упругого удара тележек и запишем данные в таблицу 2.
Таблица 2
Результаты измерений и расчетов для абсолютно упругого удара
| Номер измерения | 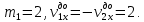 | ||||
| m2, кг | 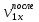 , м/с , м/с | 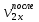 , м/с , м/с | 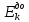 , Дж , Дж | 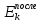 , Дж , Дж | |
| 1 | 1 | -0,7 | 3,3 | 6,00 | 5,90 |
| 2 | 2 | -2,00 | 2,00 | 8,00 | 8,00 |
| 3 | 3 | -2,8 | 1,2 | 10,00 | 10,00 |
| 4 | 4 | -3,3 | 0,7 | 12,00 | 11,87 |
| 5 | 5 | -3,7 | 0,3 | 14,00 | 13,92 |
| 6 | 6 | -4,00 | 0,00 | 16,00 | 16,00 |
| 7 | 7 | -4,2 | -0,2 | 18,00 | 17,78 |
| 8 | 8 | -4,4 | -0,4 | 20,00 | 20,00 |
| 9 | 9 | -4,5 | -0,5 | 22,00 | 21,38 |
| 10 | 10 | -4,7 | -0,7 | 24,00 | 24,54 |
-
Рассчитаем кинетические энергии системы до и после соударения по формулам
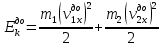
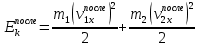
Полученные значения занесем в таблицу 2.
Вывод: Из таблицы 2 видно что, при абсолютно упругом столкновении кинетическая энергия до столкновения равна кинетической энергии после столкновения.
Эксперимент 2. Абсолютно неупругий удар (
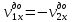 )
)-
Вывод формулы для относительной величины тепловой энергии δ при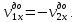
Абсолютно неупругий удар - столкновение двух тел, после которого форма и размеры тел не восстанавливаются, тела “слипаются” и движутся как одно целое с одной скоростью. Суммарный импульс двух неупруго сталкивающихся тел сохраняется, а кинетическая энергия становится меньше, так как часть энергии переходит в конечном итоге в тепловую:
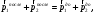
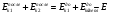
Используя, определение импульса и определение абсолютно неупругого удара, преобразуем закон сохранения импульса, спроектировав его на ось
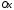 , вдоль которой движутся тела, в следующее уравнение:
, вдоль которой движутся тела, в следующее уравнение: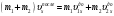
а закон для кинетической энергии преобразуем в такое уравнение:
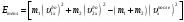 .
.Помножив и разделив второе уравнение на
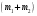 и используя первое уравнение, получим:
и используя первое уравнение, получим: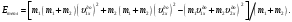
Относительная величина тепловой энергии
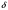 равна отношению
равна отношению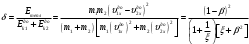 ,
,где
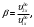
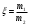 .
.Если
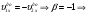
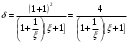
-
Проведем измерения и расчет ξ,
и расчет ξ,  и
и  для абсолютно неупругого удара тележек при
для абсолютно неупругого удара тележек при  и запишем данные в таблицу 3.
и запишем данные в таблицу 3.
Таблица 3
Результаты измерений и расчетов для абсолютно неупругого удара
| Номер измерения | 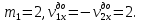 | |||||||
| m2, кг | 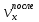 , м/с , м/с |  , Дж , Дж |  , Дж , Дж | 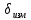 | 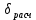 | β | ξ | |
| 1 | 1 | 0,7 | 6,00 | 0,73 | 0,88 | 0,88 | -1 | 2,00 |
| 2 | 2 | 0,0 | 8,00 | 0,00 | 1,00 | 1,00 | -1 | 1,00 |
| 3 | 3 | -0,4 | 10,00 | 0,40 | 0,96 | 0,96 | -1 | 0,60 |
| 4 | 4 | -0,7 | 12,00 | 1,47 | 0,88 | 0,88 | -1 | 0,50 |
| 5 | 5 | -0,9 | 14,00 | 2,84 | 0,80 | 0,80 | -1 | 0,40 |
| 6 | 6 | -1,0 | 16,00 | 4,00 | 0,75 | 0,75 | -1 | 0,33 |
| 7 | 7 | -1,1 | 18,00 | 5,45 | 0,70 | 0,70 | -1 | 0,29 |
| 8 | 8 | -1,2 | 20,00 | 7,20 | 0,64 | 0,64 | -1 | 0,25 |
| 9 | 9 | -1,3 | 22,00 | 9,30 | 0,58 | 0,58 | -1 | 0,22 |
| 10 | 10 | -1,3 | 24,00 | 10,14 | 0,57 | 0,57 | -1 | 0,20 |
-
Рассчитаем по формуле
по формуле
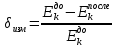
-
Рассчитаем по выведенной формуле и внесем значения в таблицу 3.
по выведенной формуле и внесем значения в таблицу 3. -
Построим график зависимости δ(ξ).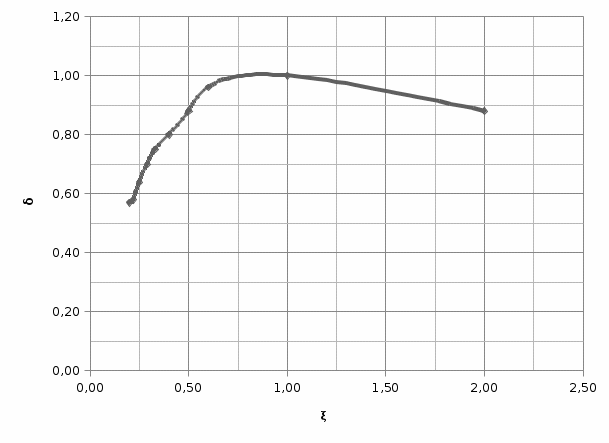
Вывод: При абсолютно неупругом ударе при равенстве масс и скоростей сталкивающихся тел кинетическая энергия равна нулю и полностью переходит в тепловую, а с ростом массы второго тела направление движения ударившихся тел меняется на противоположное и все большее количество кинетической энергии переходит в тепловую и относительная величина тепловой энергии
 стремится к 1.
стремится к 1. Эксперимент 3. Абсолютно неупругий удар при m1 = m2.
-
Вывод формулы для относительной величины тепловой энергии δ при m1 = m2
Относительная величина тепловой энергии
 равна отношению:
равна отношению: ,
,где

 .
.Если
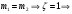

-
Проведем измерения и расчет β,
и расчет β,  и
и  для абсолютно неупругого удара тележек при m1 = m2 и запишем данные в таблицу 4.
для абсолютно неупругого удара тележек при m1 = m2 и запишем данные в таблицу 4.
Таблица 4
Результаты измерений и расчетов для абсолютно неупругого удара
| Номер измерения | 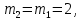 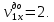 | |||||||
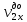 , м/с , м/с |  , м/с , м/с |  , Дж , Дж |  , Дж , Дж |  |  | β | ξ | |
| 1 | 0 | 1 | 4,00 | 2,00 | 0,50 | 0,50 | 0,00 | 1 |
| 2 | -0,2 | 0,9 | 4,04 | 1,62 | 0,60 | 0,60 | -0,10 | 1 |
| 3 | -0,4 | 0,8 | 4,16 | 1,28 | 0,69 | 0,69 | -0,20 | 1 |
| 4 | -0,6 | 0,7 | 4,36 | 0,98 | 0,78 | 0,78 | -0,30 | 1 |
| 5 | -0,8 | 0,6 | 4,64 | 0,72 | 0,84 | 0,84 | -0,40 | 1 |
| 6 | -1 | 0,5 | 5,00 | 0,50 | 0,90 | 0,90 | -0,50 | 1 |
| 7 | -1,2 | 0,4 | 5,44 | 0,32 | 0,94 | 0,94 | -0,60 | 1 |
| 8 | -1,4 | 0,3 | 5,96 | 0,18 | 0,97 | 0,97 | -0,70 | 1 |
| 9 | -1,6 | 0,2 | 6,56 | 0,08 | 0,99 | 0,99 | -0,80 | 1 |
| 10 | -1,8 | 0,1 | 7,24 | 0,02 | 1,00 | 1,00 | -0,90 | 1 |
-
Рассчитаем по формуле
по формуле

-
Рассчитаем по выведенной формуле и внесем значения в таблицу 3.
по выведенной формуле и внесем значения в таблицу 3. -
Построим график зависимости δ(β).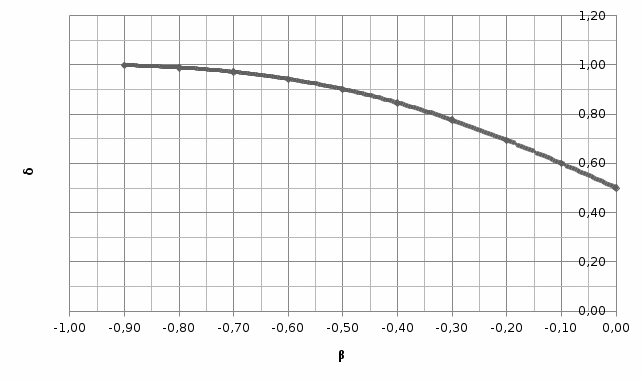
Вывод: При равенстве масс, сталкивающихся тел и с увеличением скорости второго тела кинетическая энергия столкнувшихся тел уменьшается, а тепловая энергия возрастает.