Файл: Практическое задание 2 (вариант 5) Граничные условия в электростатическом поле.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.12.2023

Просмотров: 153

Скачиваний: 10

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 2 (вариант 5)Граничные условия в электростатическом полеЗаданиеРассматривается двухслойный плоский конденсатор, подключенный к источнику напряжения U (см. рис. 1). Заданы пробивные напряженности слоев Епроб1 и Епроб2.Требуется:– рассчитать напряженность 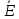, электрическое смещение 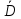, поляризацию 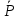для каждого слоя конденсатора;– определить плотность свободных зарядов σна обкладках конденсатора и плотность связанных зарядов σсвяз на границе раздела диэлектриков;– определить электрическую емкость конденсатора на единицу площади;– рассчитать пробивное напряжение Uпроб.– построить график распределения потенциала φ вдоль оси x.Ответы привести к размерности: E1 , E2 – [кВ/см]; D1, D2, P1, P2, σ, σсвяз– [пКл/см2];Uпроб. 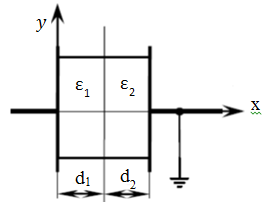– [кB];C – [пФ/см2].Сделать необходимые выводы.Рис. 1. Двухслойный конденсаторТаблица 1 – Исходные данные

Вариант
U, кВ
Епроб1 , кВ/см
Епроб2 , кВ/см
d1, см
d2, см
1
2

5Д
15
16
32
3,0
7,0
2
1
Решение.Линии напряженности электрического конденсатора перпендикулярны этим обкладкам от одной обкладки к другой. Выразим и определим напряженность, создаваемую свободными зарядами.
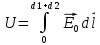
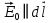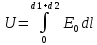
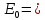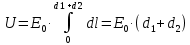
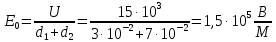
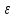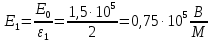
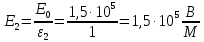
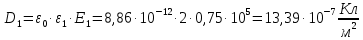
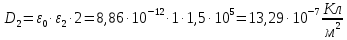
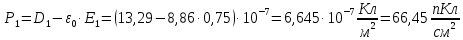
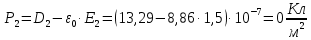
Так как, ,то можно перейти от векторов к скалярным величинам:В конденсаторе поле между обкладками однородно ( const), следовательно:Значит:Рассчитаем напряженность в области диэлектриков с разными :Рассчитаем электрическую индукцию в каждом из диэлектриков:Рассчитаем поляризованность каждого из диэлектриков:Так как, 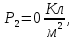то 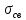(поверхностная плотность свободного заряда на границе раздела диэлектриков) создается только вторым диэлектриком: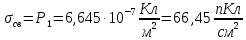Для свободных зарядов на обкладках: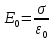Выразим 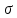из формулы: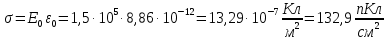Представим конденсатор с двумя диэлектриками в виде схемы последовательного соединения двух конденсаторов, в каждом из которых содержится по одному диэлектрику.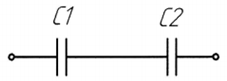Рисунок 2 - Преобразование конденсатора с двумя диэлектриками в схему последовательного соединения двух конденсаторов. 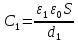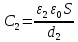; Рассчитаем

результирующую емкость конденсаторов, соединенных последовательно:



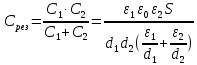
Рассчитаем удельную емкость данного конденсатора, приходящуюся на единицу площади обкладки:



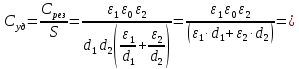
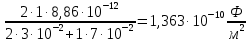= 0,01363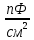

Рассчитаем напряженности электрического поля, созданного свободными зарядами, при которых напряженность поля в диэлектрике будет равна пробивному значению и пробивное напряжение конденсатора:







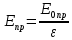
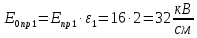
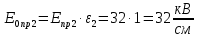
Сравним полученные напряженности электрического поля свободных зарядов между собой. Они равны, поэтому для расчета пробивного напряжения используем:





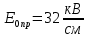
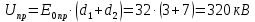
Составим уравнения для вычисления потенциала в различных областях конденсатора.

По формуле связи между напряженностью и потенциалом:



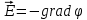
Так как между обкладками конденсатора величина потенциала изменяется только вдоль оси :



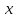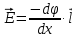
Так как вектор напряженности сонаправлен с осью 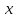, перейдем от векторных единиц к их модулям: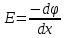





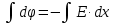
Учтем, что поле между обкладками конденсатора - однородное.



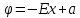
В первом диэлектрике:



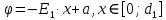
Вычислим значение постоянной интегрирования :



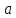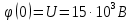
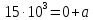
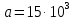
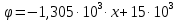
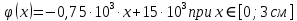
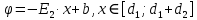
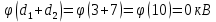
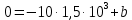
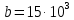
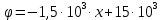
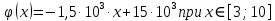
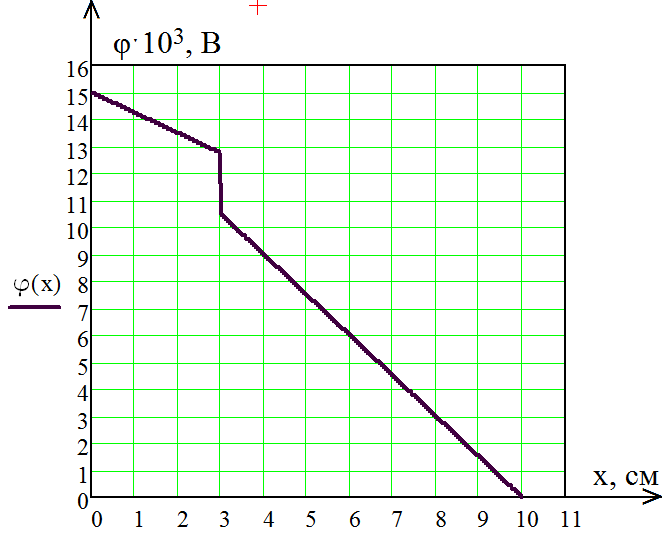
Запишем уравнения для потенциала в различных областях конденсатора.Для области первого диэлектрика:Во втором диэлектрике:Вычислим значение постоянной интегрирования b:Для области второго диэлектрика:График зависимости 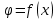для всех областей конденсатора на одной координатной плоскости изображен на рис.3.Вывод: в результате выполнения работы получены навыки расчета параметров электрического поля внутри конденсатора, емкости конденсатора, содержащего между обкладками более одного диэлектрика и влияние неоднородности диэлектрика между обкладками на распределение потенциала. 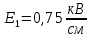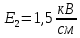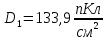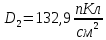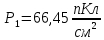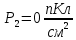Рассчитаны следующие величины: Напряженность электрического поля в области первого диэлектрика:Напряженность электрического поля в области второго диэлектрика:Электрическая индукция в области первого диэлектрика:Электрическая индукция в области второго диэлектрика:Поляризованность первого диэлектрика:Поляризованность второго диэлектрика:Поверхностную плотность свободного заряда на границе раздела диэлектриков: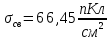Поверхностную плотность заряда на обкладках:
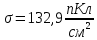
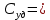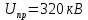
Удельную емкость конденсатора на единицу площади обкладки: = 0,01363 Пробивное напряжение для данного конденсатора: ˑРисунок 3 Зависимости двухслойного конденсатора Вывод: электрический потенциал имеет скачкообразное изменение на границе раздела слоев.

Смотрите также файлы