Файл: Лабораторная работа 2 по дисциплине Компьютерная графика Студент Группа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
| Кафедра | Вычислительной техники |
Лабораторная работа №2 по дисциплине
«Компьютерная графика»
| Студент: |
| Группа: |
| Преподаватель: |
Новосибирск
2023
Цель работы
Построить линию пересечения двух пересекающихся треугольников двумя способами.
-
используя общее уравнение плоскости; -
используя параметрическое уравнение плоскости.
Принцип работы
Способы нахождения пересечения двух треугольников:
-
с помощью общих уравнений плоскостей треугольников:
Уравнение прямой пересечения представляется как система из общих уравнений плоскостей треугольников, далее находится уравнение плоскости, содержащее сторону 1-ого треугольника и пересекающее плоскость 2-ого, данное уравнение плоскости добавляется в систему общих уравнений плоскостей треугольников, затем вычисляются координаты точки пересечения путем решения системы уравнений.
-
c помощью параметрического уравнения прямой пересечения плоскостей треугольников:
Уравнение прямой пересечения представляется в каноническом виде (коэффициенты направляющего вектора находятся как векторное произведение нормалей к плоскостям треугольников, а точка, принадлежащая прямой, подбирается путем решения системы уравнений, содержащих общие уравнения плоскостей треугольников). Каноническое уравнение данной прямой переводится в параметрическую форму. В каноническое уравнение стороны 1-ого треугольника, пересекающей плоскость 2-ого, подставляются выраженные через параметр координаты прямой пересечения, далее вычисляется значение параметра. Вычисленное значение параметра подставляется в параметрическое уравнение прямой пересечения для
нахождения координат точки пересечения
Ход работы
Зададим координаты вершин треугольников и отобразим их вместе с нормалями к их плоскостям:

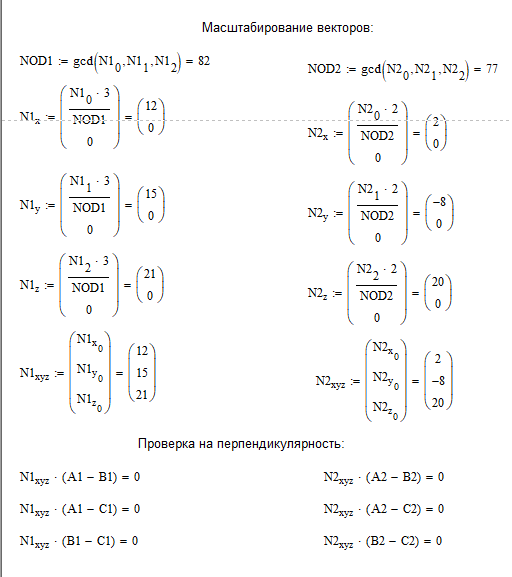
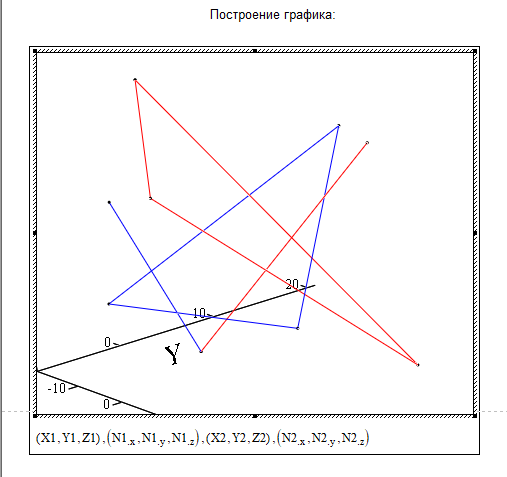
Реализация 1 способа.





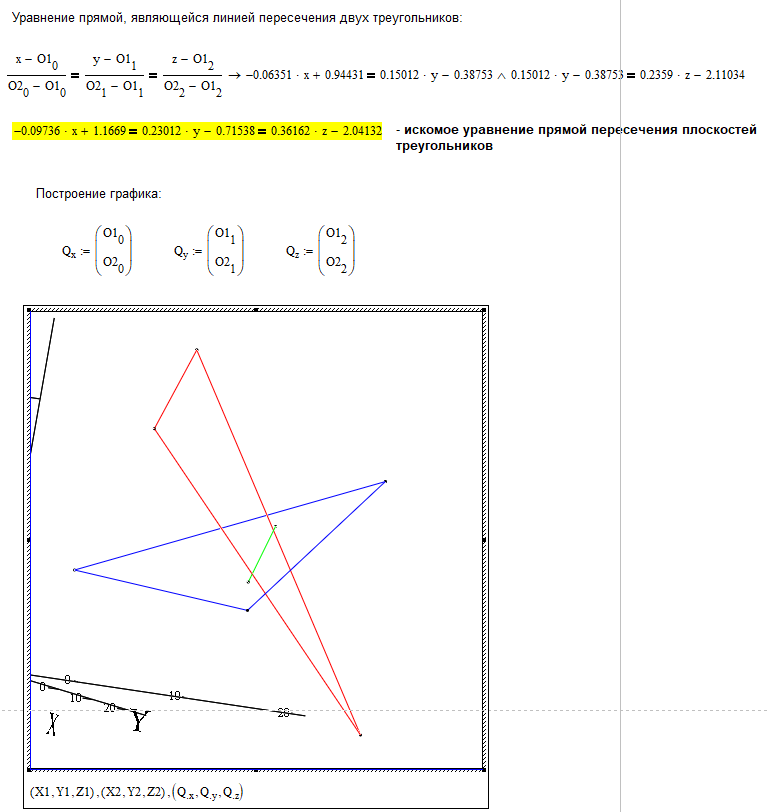
Реализация 2 способа.



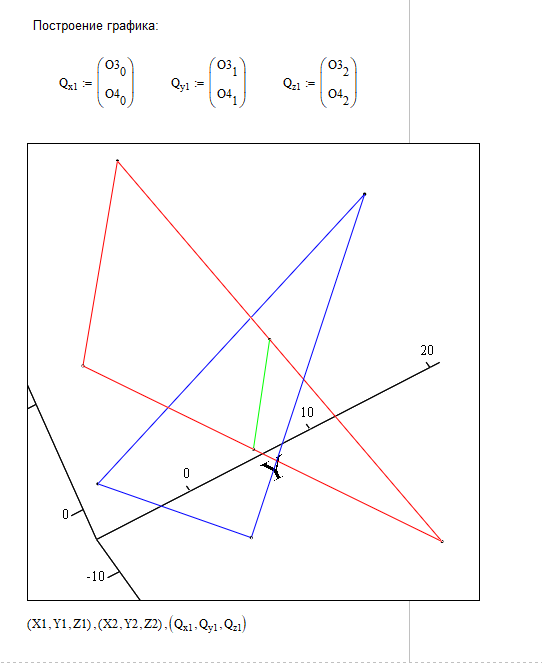
Вывод
В ходе выполнения лабораторной работы было изучено два способа построения линии пересечения двух пересекающихся треугольников: с использованием общего уравнения плоскости и с использованием параметрического уравнения плоскости. Первый метод может быть достаточно сложным в реализации и требует дополнительных вычислений. Использование параметрического уравнения плоскости позволяет более просто и эффективно вычислить точки пересечения двух треугольников. Этот метод является более точным и быстрым в реализации. Таким образом, можно сделать вывод, что использование параметрического уравнения плоскости является более предпочтительным способом при построении линии пересечения двух пересекающихся треугольников в компьютерной графике.