Лекция N 17

Метод симметричных составляющих

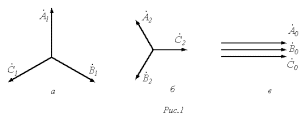
М етод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричных режимов их работы, в том числе с нестатической нагрузкой. В основе метода лежит представление несимметричной трехфазной системы переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех симметричных систем, которые называют симметричными составляющими. Различают симметричные составляющие прямой, обратной и нулевой последовательностей, которые различаются порядком чередования фаз.Симметричную систему прямой последовательности образуют (см. рис. 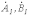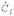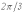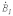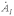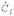1,а) три одинаковых по модулю вектора и со сдвигом друг по отношению к другу на рад., причем отстает от , а - от 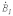. 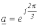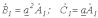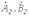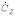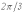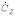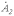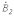Введя, оператор поворота , для симметричной системы прямой последовательности можно записать .Симметричная система обратной последовательности образована равными по модулю векторами и с относительным сдвигом по фазе на рад., причем теперь отстает от , а - от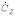

---

(см. рис. 1,б). Для этой системы имеем

.

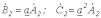Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе (см. рис. 1,в):

.

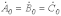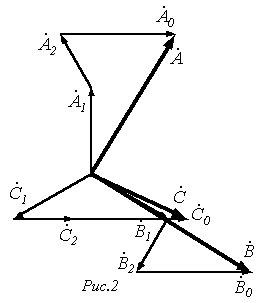
При сложении трех указанных систем векторов получается несимметричная система векторов (см. рис. 2).

Любая несимметричная система однозначно раскладывается на симметричные составляющие. Действительно,

;

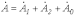(1)

;

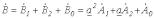(2)

.

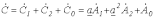(3)

Таким образом, получена система из трех уравнений относительно трех неизвестных 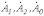, которые, следовательно, определяются однозначно. Для нахождения 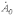сложим уравнения (1)…(3). Тогда, учитывая, что 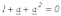, получим

.

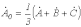(4)

Для нахождения 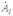умножим (2) на 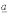, а (3) – на 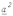, после чего полученные выражения сложим с (1). В результате приходим к соотношению

.

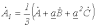(5)

Для определения с соотношением (1) складываем уравнения (2) и (3), предварительно умноженные соответственно на 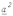и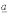

---

. В результате имеем:

.

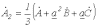(6)

Формулы (1)…(6) справедливы для любой системы векторов 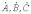, в том числе и для симметричной. В последнем случае 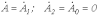.В заключение раздела отметим, что помимо вычисления симметричные составляющие могут быть измерены с помощью специальных фильтров симметричных составляющих, используемых в устройствах релейной защиты и автоматики.Свойства симметричных составляющих токов
и напряжений различных последовательностейРассмотрим четырехпроводную систему на рис. 3. Для т ока в нейтральном проводе имеем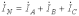 .Тогда с учетом (4)

,

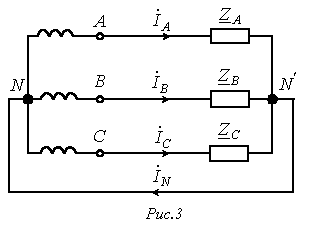
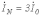(7)

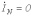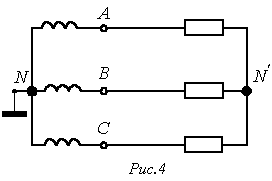
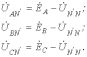
т.е. ток в нейтральном проводе равен утроенному току нулевой последовательности.Если нейтрального провода нет, то и соответственно нет составляющих тока нулевой последовательности.Поскольку сумма линейных напряжений равна нулю, то в соответствии с (4) линейные напряжения не содержат составляющих нулевой последовательности.Рассмотрим трехпроводную несимметричную систему на рис. 4.ЗдесьТогда, просуммировав эти соотношения, для симметричных составляющих нулевой последовательности фазных напряжений можно записать 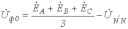.Если система ЭДС генератора симметрична, то из последнего получаем

.

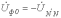(8)

Из (8) вытекает:

• 
  в фазных напряжениях симметричного приемника отсутствуют симметричные составляющие нулевой последовательности;
  
• 
  симметричные составляющие нулевой последовательности фазных напряжений несимметричного приемника определяются величиной напряжения смещения нейтрали;
  
• 
  фазные напряжения несимметричных приемников, с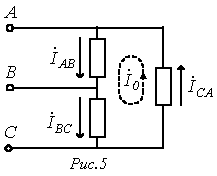 оединенных звездой, при питании от одного источника различаются только за счет симметричных составляющих нулевой последовательности; симметричные составляющие прямой и обратной последовательностей у них одинаковы, поскольку однозначно связаны с соответствующими симметричными составляющими линейных напряжений.
  

---

При соединении нагрузки в треугольник фазные ток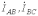и и 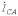могут содержать симметричные составляющие нулевой последовательности 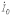. При этом 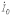(см. рис. 5) циркулирует по контуру, образованному фазами нагрузки.Сопротивления симметричной трехфазной цепи
для токов различных последовательностейЕсли к симметричной цепи приложена симметричная система фазных напряжений прямой (обратной или нулевой) последовательностей, то в ней возникает симметричная система токов прямой (обратной или нулевой) последовательности. При использовании метода симметричных составляющих на практике симметричные составляющие напряжений связаны с симметричными составляющими токов той же последовательности. 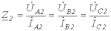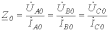Отношение симметричных составляющих фазных напряжений прямой (обратной или нулевой) последовательности к соответствующим симметричным составляющим токов называется комплексным сопротивлением прямой ,обратнойи нулевойпоследовательностей.Пусть имеем участок цепи на рис. 6. Для фазы А этого участка можно записать

.

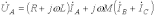(9)

Тогда для симметричных составляющих прямой и обратной последовательностей с учетом, того, что 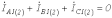, на основании (9) имеем  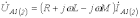 .О 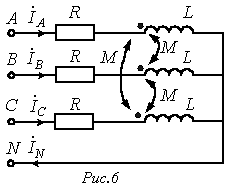тсюда комплексные сопротивления прямой и обратной последовательностей одинаковы и равны: 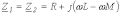.Для симметричных составляющих нулевой последовательности с учетом равенства 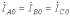соотношение (9) трансформируется в уравнение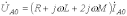

---

,

откуда комплексное сопротивление нулевой последовательности

.

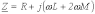В рассмотренном примере получено равенство сопротивлений прямой и обратной последовательностей. В общем случае эти сопротивления могут отличаться друг от друга. Наиболее типичный пример – различие сопротивлений вращающейся машины для токов прямой и обратной последовательностей за счет многократной разницы в скольжении ротора относительно вращающегося магнитного поля для этих последовательностей. 

 

Применение метода симметричных составляющих
для симметричных цепей

Расчет цепей методом симметричных составляющих основывается на принципе наложения, в виду чего метод применим только к линейным цепям. Согласно данному методу расчет осуществляется в отдельности для составляющих напряжений и токов различных последовательностей, причем в силу симметрии режимов работы цепи для них он проводится для одной фазы (фазы А). После этого в соответствии с (1)…(3) определяются реальные искомые величины. При расчете следует помнить, что, поскольку в симметричном режиме ток в нейтральном проводе равен нулю, сопротивление нейтрального провода никак ни влияет на симметричные составляющие токов прямой и обратной последовательностей. Наоборот, в схему замещения для нулевой последовательности на основании (7) вводится утроенное значение сопротивления в нейтральном проводе. С учетом вышесказанного исходной схеме на рис. 7,а соответствуют расчетные однофазные цепи для прямой и обратной последовательностей (рис. 7,б) и нулевой последовательности (рис. 7,в).



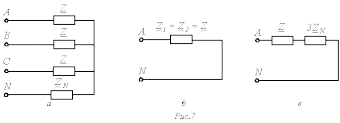
Существенно сложнее обстоит дело при несимметрии сопротивлений по фазам. Пусть в цепи на рис. 3 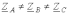. Разложив токи на симметричные составляющие, для данной цепи можно записать

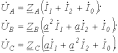(10)

В свою очередь

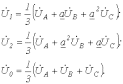(11)

Подставив в (11) значения соответствующих параметров из (10) после группировки членов получим

---

Смотрите также файлы

• 1. Что называют отношением двух чисел Приведите пример. Как можно записать отношение чисел а и b.docx

• Университет синергия Направление подготовки 38.docx

• Практическая работа к теме Страна патриотизм Тема занятия День народного единства. Что мы Родиной зовем Класс 57 классов.docx

• білас Саынов атындаы араанды техникалы университеті Апараттыесептеуіш жйелер кафедрасы.docx

• О применении судами общей юрисдикции общепризнанных принципов и норм международного права и международных договоров рф.doc