Добавлен: 06.12.2023
Просмотров: 30
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Муниципальное казеное образовательное учреждение
Сергокалинская СОШ № 2»им. Героя России М.Нурбагандова
ОБЪЁМНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
проектная работа
Выполнила:
Шахбанова Заира
ученица 6 г класса
Руководитель:
Тагирова Р.М.
СЕРГОКАЛА 2022г.
Содержание
Введение…………………………………………………………..
I. Теоретическая часть.
1.Что такое геометрические фигуры?...........................................
2.Связь плоских и объёмных геометрических фигур……………
II.Практическая часть.
1.План изготовления объёмных геометрических фигур…………
Заключение……………………………………………………....
Список литературы………………………………………………
Введение
Актуальность.
Геометрия имеет большое значение для развития мышления и воображения ребёнка. Окружающие нас предметы имеют в корне своего строения именно объёмную геометрическую фигуру. Для многих профессий знания объёмных геометрических фигур являются основополагающими. Поэтому я решила выбрать тему «Объёмные геометрические фигуры».
Цель: узнать, как самостоятельно изготовить объёмные геометрические фигуры.
Задачи:
1.Изучить литературу по заданной теме
2. Составить план изготовления объёмной геометрической фигуры
3.Сделать и оформить выводы
I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. Что такое геометрические фигуры
Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
Прямая
Это фигура полностью размещается в одной плоскости. Она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол
Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Четырехугольники
Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат – это четырехугольник с равными сторонами и углами.
Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда.
Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом отрезок, соединяющий центр и замкнутую линию (окружность), принято называть радиусом.
Интересный факт: если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
Треугольник
Это простая геометрическая фигура. Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
К этой категории стоит отнести геометрические фигуры разнообразных форм, ломаная линия контуров которых замыкается.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
К этой категории причисляют следующие конструкции:
куб;
призма;
сфера;
цилиндр;
пирамида;
тор,
конус.
В переводе с греческого языка термин «конус» обозначает сосновую шишку.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
2. Как связаны между собой объемные и плоские геометрические фигуры?
Объемные и плоские геометрические фигуры тесно связаны между собой.
Если плоскую геометрическую фигуру вращать вокруг оси, образуется объемная геометрическая фигура. Такие фигуры еще называют телами вращения. Так образуются конус, сфера, цилиндр, тор.
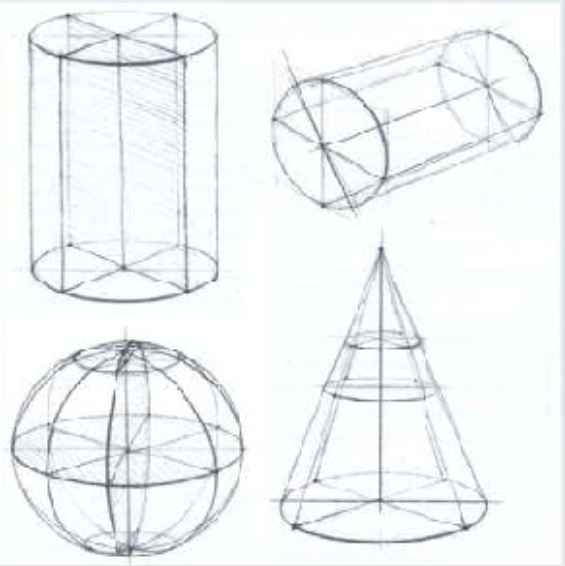
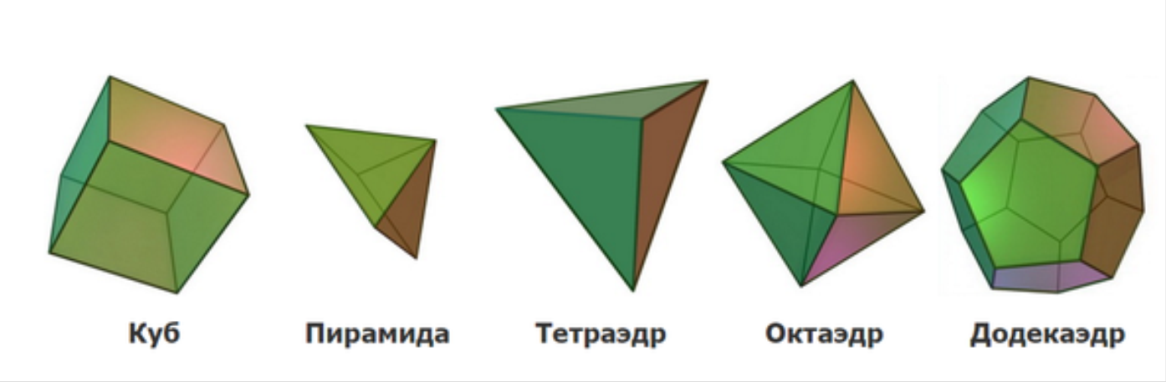
Еще бывают объемные геометрические фигуры, поверхность которых ограничена плоскими геометрическими фигурами. Например, куб имеет квадратные грани, пирамида – треугольные, призма – прямоугольниками и т.д.
II. ПРАКТИЧЕСКАЯ ЧАСТЬ
План изготовления объёмной геометрической фигуры
В первую очередь необходимо вооружиться подручными средствами: бумагой, линейкой, карандашом, ножницами, клеем.
Далее необходимо построить чертеж. Такой чертеж называется разверткой. Его построить достаточно сложно. Нужно точно откладывать размеры и размечать линии сгибов. Это под силу тем, кто уже изучал в школе черчение. Гораздо проще распечатать готовую развертку на принтере.
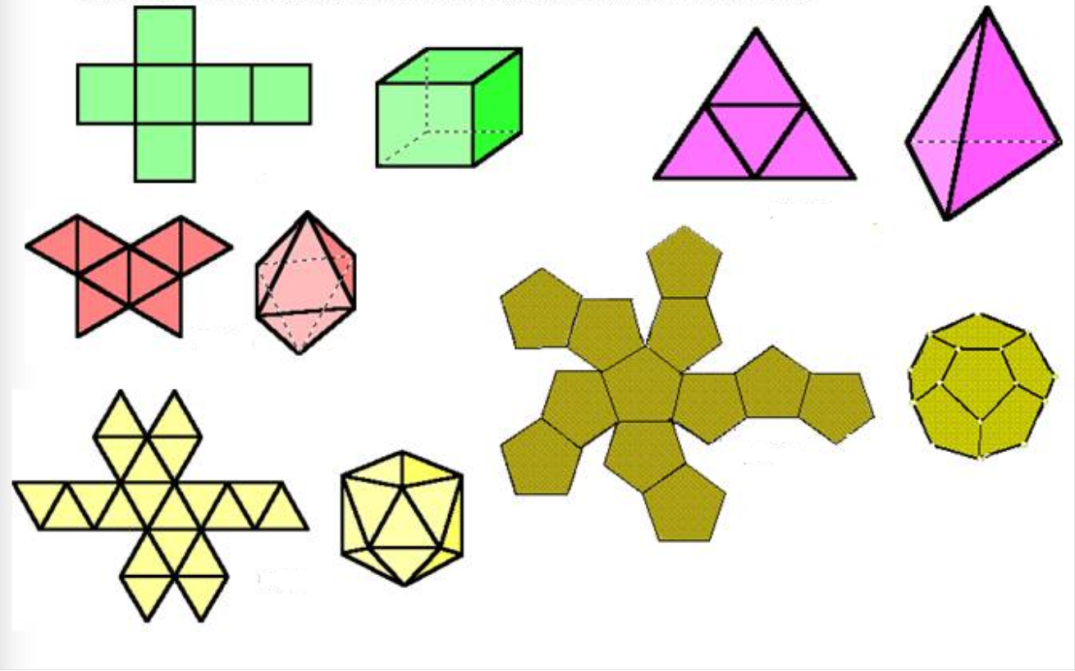
У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.д. Для любого выпуклого многогранника имеет место равенство:
B – P + Г = 2
где В – число вершин, Р – число ребер, Г – число граней многогранника.
Далее вырезаем заготовку по контуру. Обязательно необходимо предусмотреть участки для склеивания фигуры.
После этого нужно согнуть шаблон по линиям сгиба. Чтобы линия сгиба была ровной и острой, можно воспользоваться металлической линейкой.
Остается аккуратно склеить фигуру.
Заключение.
Выполняя эту работу, меня очень захватил процесс конструирования этих моделей. Для этого мне понадобились такие качества, как усидчивость, старательность, внимательность, ловкость рук. Но самое главное, это чувство радости от того, что у тебя получается.
В ходе работы над проектом, я училась самостоятельно искать ответы на вопросы, училась сотрудничать с родителями, братом. Училась преодолевать себя ради себя самой. Я училась задавать вопросы и обрабатывать анкеты, делать выводы.
В результате, я узнала алгоритм изготовления объёмных геометрических фигур.
Моя гипотеза о том, что если у фигуры 4 угла, значит это объёмная фигура не подтвердилась. Ведь у объёмных может быть и углов больше, а 4 угла может иметь и плоский прямоугольник.
Я сделала свой первый шаг в мир геометрии. Это только начало. В дальнейшем я бы хотела бы исследовать предметы, которые строятся на основе этих объёмных геометрических фигур. Но это тема уже следующего проекта.