Файл: Лабораторная работа 4 По дисциплине Разведочная геофизика Тема " Исследование структуры экспериментального сигнала с прогнозом ".docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Санкт-Петербургский горный университет»
Кафедра геофизических и геохимических методов поисков и разведки месторождений полезных ископаемых
ЛАБОРАТОРНАЯ РАБОТА №4
По дисциплине: Разведочная геофизика
Тема: "Исследование структуры экспериментального сигнала с прогнозом"
(подпись) (Ф.И.О.)
(подпись) (Ф.И.О.)
Санкт-Петербург
2021
Аннотация
Сегодня, чтобы получить инженерно-геологические сведения, необходимые для прогнозирования инженерно-геологической обстановки определенного земельного участка, применяется множество разнообразных технологий изысканий. На различных стадиях инженерно-геологических исследований может использоваться одновременно несколько методик анализа геологической среды. Составление формализованных моделей природно-технических систем в отсутствии фактических данных один из оптимальных способов представления всей картины требуемой ситуации. Опираясь на математические модели, можно сделать прогноз без подробной информации, то есть отсутствие съёмок, измерений, показателей и так далее в однородной среде. В неоднородной среде без минимальных данных обойтись будет гораздо сложнее, однако без подробнейшей рекогносцировки, несомненно, возможно изобразить определённый план, который требуется в настоящий момент.
Всё это можно отнести к разряду ранней диагностики, когда требуется определиться с масштабом планируемых изысканий на местности, финансового расчёта, поиска лучшего способа проведения исследований, а также геологических, геодезических, геофизических работ. Нельзя не отметить также оценку чрезвычайных ситуаций, когда присутствует необходимость моментального реагирования и устранения проблемы – это может быть экологическая катастрофа, природно-стихийные бедствия; прогноз сейсмической ситуации жилой, промышленной зон, а также в труднодоступной местности для рентабельности проводимых работ и безопасности человека и окружающей среды.
Одним словом, современное положение, начиная от экологии, заканчивая геополитическими и экономическими факторами заставляет человеческое общество более вдумчиво распределять ресурсы. Другими словами, без теоретической базы и модельных представлений, проведение любых работ считается необоснованным и вредит как планете, так и социуму и конкретно отдельно взятого человека.
Содержание
Введение
Жизнь любого человека сопровождается процессами моделирования и различными моделями. Использование различных учебных пособий, макетов в школьные годы, проведение лабораторных экспериментов, расчетов в студенческие годы, разработка чертежей, проектирование и расчет реальных устройств и процессов, построение теорий различного рода и назначения – примеры использования моделей и моделирования, когда реальные объекты и процессы заменяются их отображениями (моделями, описаниями и т. д.). Если кратко охарактеризовать моделирование, то оно заключается в замене реальной системы (процесса, явления) моделью, которая находится с ней (с ними) в некотором соответствии и способна воспроизводить интересующие исследователя свойства или характеристики реальной системы.
Безусловно, моделирование является не единственным методом изучения окружающего нас мира. Но роль моделирования в науке, в исследованиях инженерных, организационных, экономических объектов и систем и, вообще, в жизни человека, весьма велика. Можно утверждать: познание любого объекта, системы, процесса, явления сводится, по существу, к созданию его (ее) модели. Познание и изучение окружающего нас мира можно осуществлять различными способами и методами. Но при исследовании различных сложных объектов, явлений, процессов, при создании, организации и оптимизации сложных систем метод моделирования является одним из самых мощных методов. Так, перед изготовлением любого технического устройства или сооружения разрабатывается его модель-проект, человек, прежде чем совершить что-либо, обдумывает возможную последовательность действий и возможные последствия этих действий, организуя взаимодействие множества объектов, т.е. организуя деятельность некоторой системы, человек организует систему так, чтобы получить максимальный эффект от деятельности такой системы и т.д. Причиной все более расширяющегося применения моделей является то, что процессы, происходящие в модели, можно регистрировать, проверять их соответствие результатам теоретического анализа, заменять аналитические расчеты процессов их непосредственным наблюдением, т. е. эффективно решать все основные задачи экспериментального исследования.
Что такое модель? Это предельные упрощение исследования природных систем с целью их формального описания. Тогда как математическое моделирование – это знаковое моделирование, при котором описание объекта осуществляется на языке математики, а исследования модели проводятся с использованием тех или иных математических методов. В настоящее время это один из самых результативных и наиболее часто применяемых методов научного познания.
Преимуществами математического моделирования по сравнению с другими видами моделирования являются:
- экономичность, сбережение ресурсов реальной системы;
- возможность моделирования гипотетических, т. е. нереализованных в природе объектов и систем;
- возможность реализации режимов, опасных или трудновоспроизводимых в реальности;
- возможность изменения масштаба времени;
- универсальность технического и программного обеспечения, наличие пакетов прикладных программ для проведения широкого круга работ;
- возможности прогнозирования и выявления общих закономерностей;
- возможности сравнительно простого многофакторного анализа.
В качестве примеров математического моделирования в различных областях человеческой деятельности можно указать расчет траекторий космических аппаратов, прогнозирование погодных явлений, расчет и проектирование машин и устройств любой сложности, моделирование процессов в экономике, использование математических моделей в медицине, биологии и многое другое.
В геофизике формализованные модели природно-технических систем, возможные без фактических данных включают в себя следующие задачи:
1. Основываясь на математических моделях получить представление о геофизических данных исследуемого объекта.
2. Производить анализ объектов находящихся вне досягаемости прямых измерений с примерными прогнозами поведения среды (актуально при ЧП).
3. Выявление поведения объекта и его влияния на внешнюю среду на долгосрочную перспективу.
4. Оптимизация ввода и обработки массивов данных об объектах изыскания.
Применение обыкновенных дифференцированных уравнений (ОДУ) в описании динамики и в прогнозе горных систем.
Постановка аналитического моделирования характеризует то, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, дифференциальных, интегральных уравнений).
При моделировании основываясь на анализе возможных данных удается получить только для сравнительно простых систем. Для сложных систем часто возникают большие математические проблемы. Для применения аналитического метода идут на существенное упрощение первоначальной модели. Однако исследование на упрощенной модели помогает получить лишь ориентировочные результаты. Аналитические модели математически верно отражают связь между входными и выходными переменными и параметрами. Но их структура не отражает внутреннюю структуру объекта.
Конечно, нахождение решений при таком моделировании оказывается исключительно ценным для выявления общих теоретических закономерностей простых линейных цепей, систем и устройств. Но его сложность резко возрастает по мере усложнения воздействий на модель и увеличения порядка и числа уравнений состояния, описывающих моделируемый объект.
Разнообразие математических моделей, используемых в науках о Земле, делает невозможным их анализ или даже просто обзор. Так, например, математическое моделирование гравитационных и магнитных полей составляет значительную часть гравиметрии и магнитометрии. Моделирование свойств среды по результатам измерения гравитационных и магнитных полей составляет значительную часть теории интерпретации данных магниторазведки и гравиразведки. То же самое можно сказать о волновых сейсмических полях, полях температур, фильтрации и движения нефти в пласте в процессе эксплуатации нефтяных и газовых месторождений и многого другого. Поэтому целью и задачей настоящей работы служат внесение ясности в принципиальные вопросы построения математических моделей в некоторых распространённых разделах наук о Земле. При многообразии задач, возникающих при моделировании в науках о Земле, можно выделить три их класса, которые называются первой, второй и третьей задачами моделирования:
1) моделирование следствий из принятых моделей среды и моделей процессов, управляющих изучаемыми следствиями;
2) моделирование среды – создание моделей среды по известным следствиям и моделям процессов, управляющих наблюдаемыми следствиями;
3) моделирование процессов по известным моделям среды и наблюдаемым следствиям этих процессов.
Также стоит упомянуть о трех главных составляющих математической модели:
-
Предельное упрощение геометрии объекта; -
Граничные начальные условия; -
ДУ описывающее, случайный процесс
Геофизические математические задачи - задачи, возникающие при анализе физических явлений, изучаемых в связи с исследованиями строения Земли. В зависимости от природы изучаемых физических явлений различают следующие виды геофизических исследований: гравиразведку, основанную на изучении гравитационного поля; магниторазведку, основанную на изучении постоянного магнитного поля; сейсморазведку, основанную на изучении распространения упругих колебаний: электроразведку, основанную на изучении электрического поля постоянного тока или переменного электромагнитного поля; радиометрию, основанную на измерении интенсивности излучения естественной или вызванной радиоактивности горных пород. Измерение полей может производиться на поверхности Земли (наземные методы), в воздухе (аэроразведка) и в скважинах (каротаж скважин).
Математические задачи, возникающие в гравиразведке и в магниторазведке, схожи. В обоих случаях прямая задача сводится к решению уравнения Пуассона или неоднородного уравнения Лапласа в близи источника:
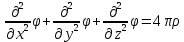, где φ – потенциал физического поля, ρ – объемная плотность физического поля.Или
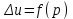- неоднородное уравнение Лапласа – уравнение Пуассона.Уравнение вида:
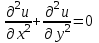или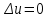 
- называется уравнением Лапласа. Оно описывает стационарный процесс с установившимся распределением температуры сплошной среды. Описывает любые установившиеся процессы. При наличии источников тепла получаем уравнение:
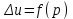- неоднородное уравнение Лапласа – уравнение Пуассона.Природный процесс существования магнитного и электрического полей основан на системе уравнений Максвелла, которые являются основополагающими для магниторазведки:
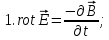
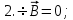
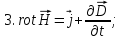
Из вышеприведённых уравнений Максвелла следует:
1) Электрическое и магнитное поля взаимосвязаны, т. е. в общем случае электрическое и магнитное поля не могут существовать независимо друг от друга. Следовательно, существует единое электромагнитное поле.
2) Уравнения Максвелла являются инвариантными относительно преобразований Лоренца, т. е. их вид не меняется при переходе от одной ИСО к другой. А также подтверждающий, что магнитных зарядов в природе не существует, магнитное поле не имеет стоков и истоков, то есть является замкнутым.
3) Уравнение показывает, что магнитные поля могу порождаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
4) Постулат Максвелла, выражающий закон создания электрических полей действием зарядов в произвольных средах.
Если рассматривать основополагающие физические законы в сейсморазведке, то сразу же вспоминаются законы оптики, а именно распространение акустической волны в однородной среде, то ее движение в общем случае описывают волновым уравнением (дифференциальным уравнением в частных производных).