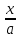Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым.



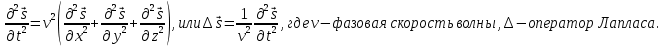
Применение данного уравнения распространяется в описании электромагнитной волны, задача малых поперечных колебаний струн, а также в описании колебательных процессов в акустических средах. Нахождение применения данного уравнения для описания гравитационных волн.

Уравнение диффузии представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным. В смысле интерпретации при решении уравнения диффузии речь идет о нахождении зависимости концентрации вещества (или иных объектов) от пространственных координат и времени, причем задан коэффициент (в общем случае также зависящий от пространственных координат и времени), характеризующий проницаемость среды для диффузии. При решении уравнения теплопроводности речь идет о нахождении зависимости температуры среды от пространственных координат и времени, причем задана теплоёмкость и теплопроводность среды (также в общем случае неоднородной).

В общем виде уравнение диффузии записывается следующим образом:



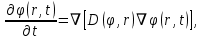
где φ(r, t) — плотность диффундирующего вещества в точке r и во время t и D(φ, r) — обобщённый коэффициент диффузии для плотности φ в точке r; ∇ — оператор набла. Если коэффициент диффузии зависит от плотности — уравнение нелинейно, в противном случае — линейно.

Если D — симметричный положительно определённый оператор, уравнение описывает анизотропную диффузию:



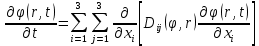
Если D постоянное, то уравнение сводится к уравнению теплопроводности:



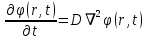
Решением уравнения диффузии будет выглядеть следующим образом:

Для одномерного случая:



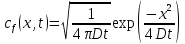
В случае произвольного начального распределения c(x, 0) общее решение уравнения диффузии представляется в интегральном виде как свёртка:



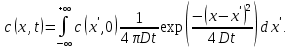
В стационарном случае уравнение диффузии сводится к решению уравнения Пуассона (неоднородное) или Лапласа (при f = 0):

---

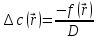
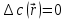
Уравнение неразрывности в дифференциальной форме

В потоках несжимаемой жидкости, в которых нет ни оттока, ни присоединения расхода, объемный расход в любом сечении постоянный. Можно поэтому предположить, что в каждой точке внутри потока должно выполняться соотношение, гарантирующее, что в ней не происходит ни исчезновения, ни возникновения жидкости. Таким уравнением является уравнение неразрывности в дифференциальной форме. Если поток в каждой точке задан вектором скорости U (x, y, z), то уравнение неразрывности будет выглядеть следующим образом:



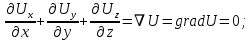
Уравнение неразрывности должно выполняться в каждой точке потока жидкости.

Решение уравнения неразрывности сводится к нахождению частных производных по трем координатам от функции трех переменных, затем находится сумма этих трех составляющих. Если полученный результат равен нулю, то справедливо судить о том, что условие неразрывности выполняется и потом жидкости может существовать.

Для аналитического моделирования характерно, что процессы функционирования системы записываются в виде некоторых функциональных соотношений (алгебраических, дифференциальных, интегральных уравнений).  Аналитическая модель может быть исследована следующими методами:

1) аналитическим, когда стремятся получить в общем виде явные зависимости для характеристик систем;

2) численным, когда не удается найти решение уравнений в общем виде и их решают для конкретных начальных данных;

3) качественным, когда при отсутствии решения находят некоторые его свойства.

Аналитические модели удается получить только для сравнительно простых систем. Для сложных систем часто возникают большие математические проблемы. Для применения аналитического метода идут на существенное упрощение первоначальной модели. Однако исследование на упрощенной модели помогает получить лишь ориентировочные результаты. Аналитические модели математически верно отражают связь между входными и выходными переменными и параметрами. Но их структура не отражает внутреннюю структуру объекта.

Например, подключив RC –цепь к источнику постоянного напряжения ε, можно составить аналитическое выражение для временной зависимости напряжения u(t) на конденсаторе C:

---

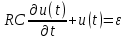
Это линейное дифференциальное уравнение (ДУ) и является аналитической моделью данной простой линейной цепи. Его аналитическое решение, при начальном условии u(0) = 0, означающем разряженный конденсатор в момент начала моделирования, позволяет найти искомую зависимость – в виде формулы:



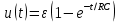
Однородные и неоднородные модели и их применимость в горном деле.
Эффективность вероятностно-статистического подхода при решении задач разведочной геофизики во многом определяется уровнем используемых при этом модельных представлений. Статистические методы ориентированы в основном на математические модели, характеризующие внешние признаки исследуемого объекта, что, в частности, типично для задач статистического оценивания. распознавания и аппроксимации. В значительно меньшей степени распространено использование стохастических (вероятностных) моделей, задающих описание внутреннего строения объекта исследования, хотя именно такие модели позволяют устанавливать особенности проявления его структуры во внешних признаках, например, в физических полях.

Стохастическое моделирование основывается на представлении о множестве, возможно, бесконечном, случайных состояний модели объекта. Такое множество может быть охарактеризовано относительно небольшим числом параметров вероятностных распределений случайных характеристик модели. Вероятностное описание определяет высокую степень параметризации, а, следовательно, и устойчивость стохастических моделей. Построение таких моделей во многом опирается на информацию, получаемую при формировании детерминированных или статистических физико-геологических моделей. Потенциальная область применения стохастических моделей при планировании геофизических экспериментов в анализе данных достаточно обширна, так как во многих случаях они позволяют получать весьма строгие решения задач, формализация которых в рамках детерминированного подхода или эмпирической статистики крайне затруднена или вообще невозможна.

Описание неоднородных геологических объектов

Существенной чертой реальных геологических тел является неоднородность их строения, которая в качественном отношении обычно отражается в описаниях структуры месторождений полезных ископаемых или в классификации пород и руд по их текстурно-структурным признакам. Естественно, что количественные оценки влияния неоднородности объекта на его свойства возможны только на основе построения его математической модели.

---

Многообразие возможных реализаций строения минерального вещества, обладающего одной и той же текстурно-структурной характеристикой, практическая невозможность задания огромного числа параметров для описания положения, геометрии и физических свойств каждой неоднородности определяют целесообразность привлечения стохастических моделей для описания сложных ситуаций. Основное преимущество таких моделей – относительно небольшое число параметров, достаточных для описания характеристик и особенностей неоднородных сред. Это свойство стохастических моделей принципиально, поскольку их параметры содержат вероятностную информацию обо всех возможных состояниях моделируемого объекта. Большинство рассматриваемых моделей в той или иной степени идеализируют реальные объекты, но даже ограниченное число предлагаемых стохастических моделей удовлетворительно аппроксимирует достаточно большое число возможных ситуаций. Примерами таких случаев могут служить модели случайных сред, объекты с неоднородным строением и др.

Представленное выше описание неоднородных геологических объектов и соответствующие стохастические модели определяют (в вероятностном смысле) физические свойства или содержания химических элементов в любой точке объекта. Во многих случаях такие «точечные» характеристики не соответствуют реальным условиям эксперимента, осуществляемого физическим устройством, всегда определяющим с той или иной разрешающей способностью эффективное (интегральное, суммарное) значение свойства для некоторой части объёма объекта. Аналогичные ситуации возникают и при вычислении обобщённых физических свойств структурно-вещественных комплексов, составляющих основу петрофизических моделей, при геохимическом и

геологическом опробовании неоднородных сред
Методика решения задачи
Н
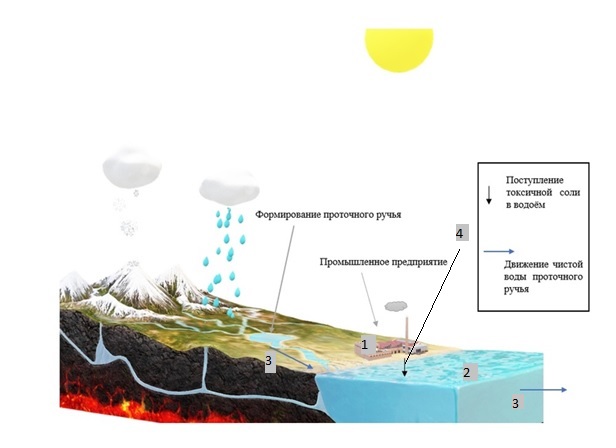
а берегу озера, объёмом V литров, расположено промышленное предприятие, выделяющее в водоём некоторое количество токсичной соли, которая равномерно распределена по всему водоёму в виде водного раствора (Рисунок 1). Концентрация токсичной соли изменятся благодаря проточному ручью, приносящий v литров чистой воды и забирающий на другом конце озера ровно такое же количество воды. Предположим, что величина поступление в водоём раствора токсичной соли от предприятия величина постоянная и не изменяется с ходом течения времени. Превосходит ли водоизмещение ручья постоянную поступления соли в водоём доподлинно неизвестно, как и сезонность протока.

---

Рисунок 1. Эскиз системы условия задачи: 1 – Предприятие, выпускающее в водоём (2) токсичную соль (поток обозначен черной стрелкой (4)); 2 – озеро, имеющее проточный ручей (поток обозначен синей стрелкой (3)); 3 – движение проточного ручья; 4 – выпуск токсичной соли.

Предположим, что предприятие выделяет постоянное количество токсичной соли, которое изменяется незначительно – это многообразные факторы, которые могут изменять концентрацию соли в водоёме (например засуха, обильные осадки, остановки производства и т. д.) Поэтому на графике (Рисунок 2), линией 1 обозначена кривая, которая предполагает погрешности, но в упрощённой модели принято считать её прямой линией, параллельной абсциссе – оси, указывающее на течение времени.


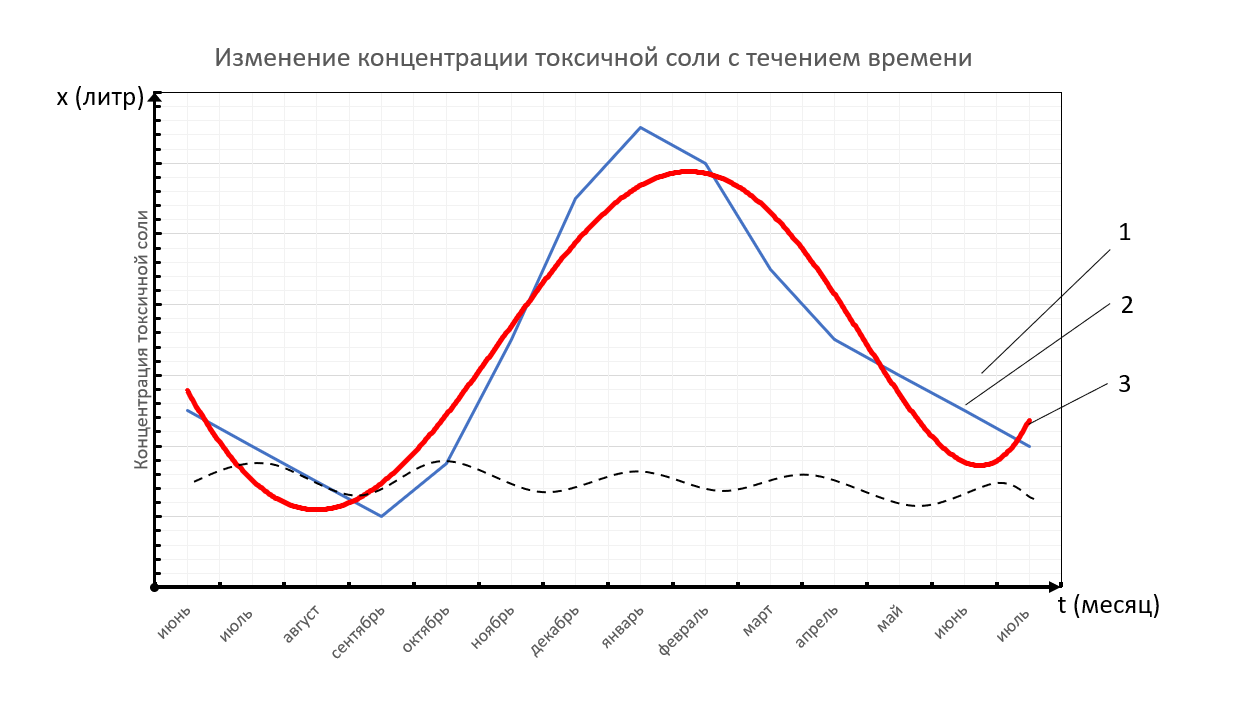
При усложнении задачи вводится климатический фактор: в сентябре температура начинает опускаться ниже отметки 0^ОС, следовательно объём проточного ручья начинает уменьшаться, в октябре объём настолько незначителен, что концентрация начинает резко увеличиваться. С ноября ручей замерзает, следовательно, содержание токсичной соли будет увеличиваться с большей скоростью. Начиная с марта, концентрация замедляет рост и начинает падение. Весной, когда скопившиеся осадками снега начинают таять, водоток резко увеличивается, поэтому происходит резкое снижение концентрации солей в озере. Для построения графика необходимо построить точки, в которых смоделированы среднемесячная концентрация выбросов предприятия. Для этого, предположим, что концентрация в августе минимальна, а в январе – максимальна. Обозначим концентрацию в августе за х, тогда концентрация в январе 6х. Содержание опасных веществ с августа по январь будет 1
Рисунок 2. Построение графической модели изменения концентрации токсичной соли в водоёме с течением времени. 1 – изменение концентрации, при постоянном сохранении условия проточности озера; 2 – график среднемесячного количества концентрации соли; 3 – изменение концентрации при усложнении задачи.

Для вычисления определённой формулы предположим, что в определённый момент времени t, в озере равномерно распределено x килограммов токсичной соли, значит, в каждом литре раствора её концентрация составляет

---

Смотрите также файлы

• Занятие 3 Преподаватель Пермь 2021.docx

• Гегель Абсолютный идеализм Род. 27 августа 1770 г в Штутгарте Учёба в Тюбингенском университете (17881793) Преподавание в Йенском университете (18011807) Директор .ppt

• Занятие 3 Преподаватель Пермь 2021 Задание Заполните таблицу Типы тканей человека.docx

• Билет 1 Части лобной кости и их поверхности.docx

• Литература по теме исследования, Интернетресурсы, Бухгалтерская (финансовая) отчетность ао 78 древообрабатывающий комбинат н. М..docx