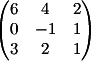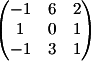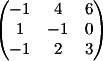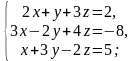Решить систему линейных уравнений:

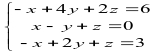
Расширенная матрица (А | b) для данной системы имеет вид Детерминант d0 = det(A) = -3 Вычисляем остальные детерминанты 1) Заменяем 1-й столбец на b Вычисляем детерминант d1 = 0 2) Заменяем 2-й столбец на b Вычисляем детерминант d2 = -3 3) Заменяем 3-й столбец на b Вычисляем детерминант d3 = -3 Вычисляем x x1 = d1/d0 = (0)/(-3) = 0 x2 = d2/d0 = (-3)/(-3) = 1 x3 = d3/d0 = (-3)/(-3) = 1 Ответ:x1 = 0

x2 = 1

x3 = 1

Вычислить частный определитель z системы

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = 27
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b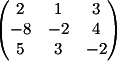



Вычисляем детерминант d₁ = -54
2) Заменяем 2-й столбец на b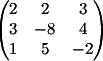



Вычисляем детерминант d₂ = 81
3) Заменяем 3-й столбец на b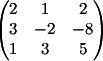



Вычисляем детерминант d₃ = 27
Вычисляем x (не обязательно)
x₁ = d₁/d₀ = (-54)/(27) = -2
x₂ = d₂/d₀ = (81)/(27) = 3
x₃ = d₃/d₀ = (27)/(27) = 1

Ответ:

x1 = -2

x2 = 3

x3 = 1

Решить систему линейных уравнений:

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -4
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b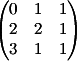



Вычисляем детерминант d₁ = -3
2) Заменяем 2-й столбец на b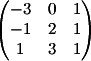



Вычисляем детерминант d₂ = -2
3) Заменяем 3-й столбец на b



Вычисляем детерминант d₃ = -7
Вычисляем x
x₁ = d₁/d₀ = (-3)/(-4) = 3/4
x₂ = d₂/d₀ = (-2)/(-4) = 1/2
x₃ = d₃/d₀ = (-7)/(-4) = 7/4

Ответ:

x1 = 3 / 4

x2 = 1 / 2

x3 = 7 / 4

Вычислить частный определитель z системы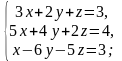

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -4
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b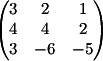



Вычисляем детерминант d₁ = -8
2) Заменяем 2-й столбец на b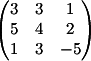



Вычисляем детерминант d₂ = 14
3) Заменяем 3-й столбец на b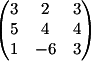



Вычисляем детерминант d₃ = -16
Вычисляем x
x₁ = d₁/d₀ = (-8)/(-4) = 2
x₂ = d₂/d₀ = (14)/(-4) = -7/2
x₃ = d₃/d₀ = (-16)/(-4) = 4

Ответ:

x1 = 2

x2 = -7 / 2

x3 = 4

Решить систему линейных уравнений:

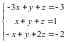
Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -4
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b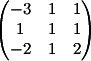



Вычисляем детерминант d₁ = -4
2) Заменяем 2-й столбец на b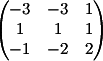



Вычисляем детерминант d₂ = -4
3) Заменяем 3-й столбец на b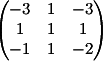



Вычисляем детерминант d₃ = 4
Вычисляем x
x₁ = d₁/d₀ = (-4)/(-4) = 1
x₂ = d₂/d₀ = (-4)/(-4) = 1
x₃ = d₃/d₀ = (4)/(-4) = -1

Ответ:

x1 = 1

x2 = 1

x3 = -1

Решить систему линейных уравнений:

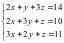
Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -12
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b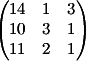



Вычисляем детерминант d₁ = -24
2) Заменяем 2-й столбец на b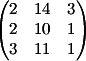



Вычисляем детерминант d₂ = -12
3) Заменяем 3-й столбец на b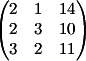



Вычисляем детерминант d₃ = -36
Вычисляем x
x₁ = d₁/d₀ = (-24)/(-12) = 2
x₂ = d₂/d₀ = (-12)/(-12) = 1
x₃ = d₃/d₀ = (-36)/(-12) = 3

Ответ:

x1 = 2

x2 = 1

x3 = 3

Частный определитель z системы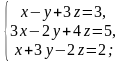 равен…

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = 15
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b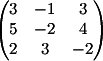



Вычисляем детерминант d₁ = 15
2) Заменяем 2-й столбец на b



Вычисляем детерминант d₂ = 15
3) Заменяем 3-й столбец на b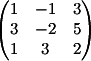



Вычисляем детерминант d₃ = 15
Вычисляем x
x₁ = d₁/d₀ = (15)/(15) = 1
x₂ = d₂/d₀ = (15)/(15) = 1
x₃ = d₃/d₀ = (15)/(15) = 1

Ответ:

---

x1 = 1

x2 = 1

x3 = 1

Решить систему линейных уравнений:

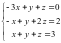
Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = 4
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b



Вычисляем детерминант d₁ = 3
2) Заменяем 2-й столбец на b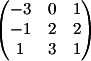



Вычисляем детерминант d₂ = 7
3) Заменяем 3-й столбец на b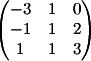



Вычисляем детерминант d₃ = 2
Вычисляем x
x₁ = d₁/d₀ = (3)/(4) = 3/4
x₂ = d₂/d₀ = (7)/(4) = 7/4
x₃ = d₃/d₀ = (2)/(4) = 1/2

Ответ:

x1 = 3 / 4

x2 = 7 / 4

x3 = 1 / 2

Решить систему линейных уравнений:

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -4
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b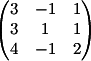



Вычисляем детерминант d₁ = 4
2) Заменяем 2-й столбец на b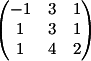



Вычисляем детерминант d₂ = -4
3) Заменяем 3-й столбец на b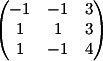



Вычисляем детерминант d₃ = -12
Вычисляем x
x₁ = d₁/d₀ = (4)/(-4) = -1
x₂ = d₂/d₀ = (-4)/(-4) = 1
x₃ = d₃/d₀ = (-12)/(-4) = 3

Ответ:

x1 = -1

x2 = 1

x3 = 3

Частный определитель x системы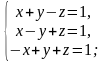 равен…

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -4
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b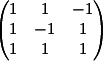



Вычисляем детерминант d₁ = -4
2) Заменяем 2-й столбец на b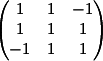



Вычисляем детерминант d₂ = -4
3) Заменяем 3-й столбец на b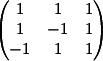



Вычисляем детерминант d₃ = -4
Вычисляем x
x₁ = d₁/d₀ = (-4)/(-4) = 1
x₂ = d₂/d₀ = (-4)/(-4) = 1
x₃ = d₃/d₀ = (-4)/(-4) = 1

Ответ:

x1 = 1

x2 = 1

x3 = 1

Решить систему линейных уравнений:

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = 4
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b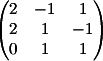



Вычисляем детерминант d₁ = 8
2) Заменяем 2-й столбец на b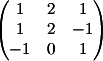



Вычисляем детерминант d₂ = 4
3) Заменяем 3-й столбец на b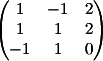



Вычисляем детерминант d₃ = 4
Вычисляем x
x₁ = d₁/d₀ = (8)/(4) = 2
x₂ = d₂/d₀ = (4)/(4) = 1
x₃ = d₃/d₀ = (4)/(4) = 1

Ответ:

x1 = 2

x2 = 1

x3 = 1

Решить систему линейных уравнений:

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -3
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b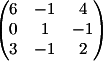



Вычисляем детерминант d₁ = -3
2) Заменяем 2-й столбец на b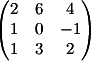



Вычисляем детерминант d₂ = 0
3) Заменяем 3-й столбец на b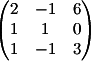



Вычисляем детерминант d₃ = -3
Вычисляем x
x₁ = d₁/d₀ = (-3)/(-3) = 1
x₂ = d₂/d₀ = (0)/(-3) = 0
x₃ = d₃/d₀ = (-3)/(-3) = 1

Ответ:

x1 = 1

x2 = 0

x3 = 1

Решить систему линейных уравнений:

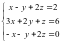
Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = 10
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b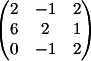



Вычисляем детерминант d₁ = 10
2) Заменяем 2-й столбец на b



Вычисляем детерминант d₂ = 10
3) Заменяем 3-й столбец на b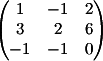



Вычисляем детерминант d₃ = 10
Вычисляем x
x₁ = d₁/d₀ = (10)/(10) = 1
x₂ = d₂/d₀ = (10)/(10) = 1
x₃ = d₃/d₀ = (10)/(10) = 1

Ответ:

x1 = 1

x2 = 1

x3 = 1

Решить систему линейных уравнений:

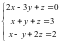
Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = 7
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b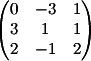



Вычисляем детерминант d₁ = 7
2) Заменяем 2-й столбец на b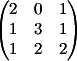



Вычисляем детерминант d₂ = 7
3) Заменяем 3-й столбец на b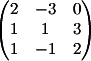



Вычисляем детерминант d₃ = 7
Вычисляем x
x₁ = d₁/d₀ = (7)/(7) = 1
x₂ = d₂/d₀ = (7)/(7) = 1
x₃ = d₃/d₀ = (7)/(7) = 1

Ответ:

---

x1 = 1

x2 = 1

x3 = 1

Частный определитель x системы равен…

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -42
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b



Вычисляем детерминант d₁ = -42
2) Заменяем 2-й столбец на b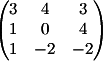



Вычисляем детерминант d₂ = 42
3) Заменяем 3-й столбец на b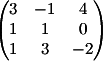



Вычисляем детерминант d₃ = 0
Вычисляем x
x₁ = d₁/d₀ = (-42)/(-42) = 1
x₂ = d₂/d₀ = (42)/(-42) = -1
x₃ = d₃/d₀ = (0)/(-42) = 0

Ответ:

x1 = 1

x2 = -1

x3 = 0

Частный определитель y системы равен…

Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -42
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b



Вычисляем детерминант d₁ = -42
2) Заменяем 2-й столбец на b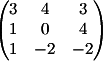



Вычисляем детерминант d₂ = 42
3) Заменяем 3-й столбец на b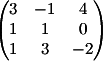



Вычисляем детерминант d₃ = 0
Вычисляем x
x₁ = d₁/d₀ = (-42)/(-42) = 1
x₂ = d₂/d₀ = (42)/(-42) = -1
x₃ = d₃/d₀ = (0)/(-42) = 0

Ответ:

x1 = 1

x2 = -1

x3 = 0

Решить систему линейных уравнений:

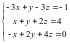
Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = -15
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b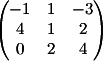



Вычисляем детерминант d₁ = -40
2) Заменяем 2-й столбец на b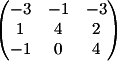



Вычисляем детерминант d₂ = -54
3) Заменяем 3-й столбец на b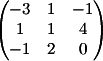



Вычисляем детерминант d₃ = 17
Вычисляем x
x₁ = d₁/d₀ = (-40)/(-15) = 8/3
x₂ = d₂/d₀ = (-54)/(-15) = 18/5
x₃ = d₃/d₀ = (17)/(-15) = -17/15

Ответ:

x1 = 8 / 3

x2 = 18 / 5

x3 = -17 / 15

Решить систему линейных уравнений:

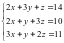
Расширенная матрица (А | b) для данной системы имеет вид
Детерминант d₀ = det(A) = 12
Вычисляем остальные детерминанты
1) Заменяем 1-й столбец на b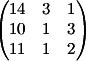



Вычисляем детерминант d₁ = 24
2) Заменяем 2-й столбец на b



Вычисляем детерминант d₂ = 36
3) Заменяем 3-й столбец на b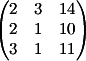



Вычисляем детерминант d₃ = 12
Вычисляем x
x₁ = d₁/d₀ = (24)/(12) = 2
x₂ = d₂/d₀ = (36)/(12) = 3
x₃ = d₃/d₀ = (12)/(12) = 1

Ответ:

x1 = 2

x2 = 3

x3 = 1

---

Смотрите также файлы

• Сканирующая зондовая микроскопия диссертация.pdf

• РЕФЕРАТ История развития следж хоккея.doc

• Термины по новой истории.doc

• Проектирование систем наведения точности для применения в сельском хозяйств.docx

• Ответ № 67 Особенности совершения таможенных операций в отношении припасов.doc