Файл: Бекітемін ыса мерзімді саба жоспары Сабаты таырыбы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 26
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Бекітемін:
Қысқа мерзімді сабақ жоспары
Сабақтың тақырыбы: Туындының анықтамасы
| Бөлім: | 10.3С Туынды | |||||||||||||
| Педагогтің Т.А.Ә.(болған жағдайда | Жеңісқанов Жан Ержанұлы | |||||||||||||
| Күні: | ___.02.2023 | |||||||||||||
| Пән/Сынып: | Алгебра, 10 ___ сынып, ЖМБ | Қатысушылар саны: 17 | Қатыспағандар саны: | |||||||||||
| Сабақтың тақырыбы: | Туындының анықтамасы | |||||||||||||
| Оқу бағдарламасына сәйкес оқыту мақсаттары: | 10.4.1.16 - аргумент өсімшесі мен функция өсімшесінің анықтамаларын білу; 10.4.1.17 - функция туындысының анықтамасын білу және анықтама бойынша функцияның туындысын табу; | |||||||||||||
| Сабақтың мақсаты: | аргумент өсімшесі мен функция өсімшесінің анықтамаларын білу; функция туындысының анықтамасын білу және анықтама бойынша функцияның туындысын табу; тұрақты функцияның және дәрежелік функцияның туындыларын табу; | |||||||||||||
| Сабақтың барысы: | ||||||||||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||||||||
| 5 минут | Ұйымдас тыру | Сәлеметсіздерме! Бүгін, Туындының анықтамасы тақырыбын қарастырамыз. Бүгінгі сабақта меңгеретініңіз: - аргумент өсімшесі мен функция өсімшесінің анықтамаларын білу; - функция туындысының анықтамасын білу және анықтама бойынша функцияның туындысын табу; Ұйымдастыру. Үй жұмысын тексеру. f функциясы берілген:
а)1; 2; -1; 1,01 нүктелерінде үздіксіз бола ма? ә) Берілген нүктелер анықталу облысының ішкі нүктелері бола ала ма? | Амандасады. Үй тапсырмасын айтады. Оқушы: функциялардың графиктерін сала отырып, оған сипаттама береді, тұжырымдар жасайды. Мұғалім: оқушыларды функцияның нүктенің аймағындағы үзіліссіздігі ұғымын түсінуге бағыт береді. | | Оқулық | |||||||||
| 10 мин | Негізгі бөлім | Жаңа сабақ Аргумент және функцияның өсімшелері ұғымдарын анықтап алайық. у=f(х) функциясы берілсін. Аргументтің х және х1 мәндері функцияның анықталу облысынан алынған. Анықтама: х1 –х айырымын аргументтің х нүктесіндегі өсімшесі д.а. Өсімшені Δх таңбасымен белгілеп, “дельта икс” деп оқиды, яғни Δх= х1 –х у=f(х) функциясының анықталу облысында тиісті кез келген х нүктесін алайық. Функцияның аргументі х-ке Δх өсімшесін берейік. Δх өсімшесін қабылдағаннан кейін аргументтің мәні (х+ Δх ) болады. Өсімшенің таңбасы оң да, теріс те болуы мүмкін. Енді функция өсімшесіне тоқталайық. Аргумент х-ке Δх өсімшесін у=f(х) функциясы да өсімше қабылдайды. Бұл функцияның өсімшесі Δу деп белгіленіп, Δу =(у+ Δу )-у немесе , Δу = f(х+Δх)-f(х) теңдігімен анықталады,сонда функция өсімшесі функцияның екі нүктедегі мәндерінің айырымына тең. Анықтама: 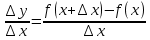 қатынасының аргумент өсімшесі Δх-тің нөлге ұмтылғандағы шегі бар болса, онда ол шекті у=f(х) функциясының х нүктесіндегі туындысы д.а. у=f(х) функциясының х нүктесіндегі туындысының белгіленуі: у'=f`(х), f`(х)-тің оқылуы: х-тен эф штрих. қатынасының аргумент өсімшесі Δх-тің нөлге ұмтылғандағы шегі бар болса, онда ол шекті у=f(х) функциясының х нүктесіндегі туындысы д.а. у=f(х) функциясының х нүктесіндегі туындысының белгіленуі: у'=f`(х), f`(х)-тің оқылуы: х-тен эф штрих.Демек, 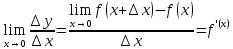 Функцияның туындысын табу амалын функцияны дифференциалдау д.а. х нүктесінде функцияның туындысы бар болса, онда f(х) функциясын осы нүктеде дифференциалданатын функция д.а. Егер функция аралықтың барлық нүктелерінде дифференциалданатын болса, онда осы аралықта дифференциалданатын функция д.а. у=f(х) функциясының х0 нүктесінде туындысы бар болса, онда осы нүктеде функция үзіліссіз болады. 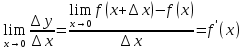 | Қосымша ақпарат көздерін пайдалана отырып түсінеді Тақырып бойынша ресурстарды қарап, танысады. Сұрақтарға жауап береді. Мысалдар қарастыру: І-топ: у=х3 функциясының аргументі х нүктесінде Δх- ке тең болғандағы өсімшесін табу ІІ-топ: у= кх+в сызықтық функциясының аргументі х-тен (х+ Δх)-ке ауысқандағы өсімшесінің аргумент өсімшесіне қатынасы к санына тең екенін дәлелдеу. Анықтама бойынша туынды табу алгоритмі: 1.Аргументке Δх өсімшесін беру; 2. Δх өсімшеге сәйкес функция өсімшесін, яғни Δу = f(х+Δх)-f(х) анықтау; 3. Функция өсімшесінің аргумент өсімшесіне қатынасын табу, яғни 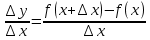 4. Соңғы теңдіктен аргумент өсімшесі нөлге ұмтылғандағы шекті анықтау: | «Екі жұлдыз бір ұсыныс» | Оқулық | |||||||||
| 25 мин | Бекіту тапсырма лары | Тапсырмалар: №1. 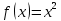 функциясының туындысын анықтайық. функциясының туындысын анықтайық.Алгоритм бойынша: 1.x+Δx; 2.Δу 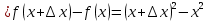 Δу 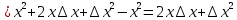 3. 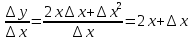 4. 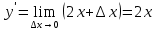 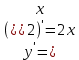 № 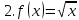 функциясының туындысын анықтайық. функциясының туындысын анықтайық.Шешуі:Туындының анықтамасын қолданамыз: 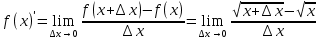 Бөлшектің алымы мен бөлімін 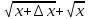 өрнегіне көбейтеміз және ( өрнегіне көбейтеміз және (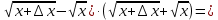 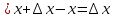 болатынын ескереміз. Сонда: болатынын ескереміз. Сонда: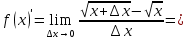 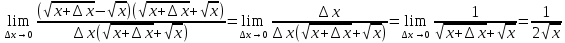 Жауабы: 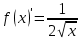 Оқулықтан №39.1, №39.2. Сергіту сәті. Логикалық тапсырмалар. | Есептер шығарады Берілген тапсырма бойынша өз ойларын ортаға салып, пікірлерін білдіріп, топтық талдау жасайды. Талқылау нәтижесінде өзара бір келісімге келіп есепті орындайды. Өз бетімен жұмыс. 1. Функциялардың туындысын табыңыз: 1) f(x)=9x8; 2) f(x)= 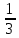 x-9 ; 3) f(x)=8· x-9 ; 3) f(x)=8·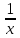 ; ; 4) f(x)=-18 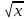 ; ;5) f(x)= -54 ; 6) f(x)=x14 – x12 + 3x9 + x3 – 9x2 +5x; 7) f(x)=2tg x + cos x– sin x; 8) f(x)=ctg x + x5- 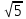 ; ;9) f(x)=sin x + 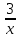 - 4x; 10) f(x)=x10· (7x + 15); - 4x; 10) f(x)=x10· (7x + 15); | Дескриптор: -аргумент өсімшесі мен функция өсімшесінің анықтамаларын біледі; - функция туындысының анықтамасын білу және анықтама бойынша функцияның туындысын таба алады. ҚБ «Екi жұлдыз бiр тiлек» әдiсi .Бiрiн-бiрi бағалау Дескриптор: - аргумент өсімшесі мен функция өсімшесінің анықтамаларын біледі;
| Интернет ресурстары Жалпы білім беретін мектептің 10–сыныбына арналған оқулық. | |||||||||
| | Жеке жұмыс | 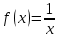 функциясының туындысын анықтайық. функциясының туындысын анықтайық.Шешуі:Туындының анықтамасын қолданамыз: 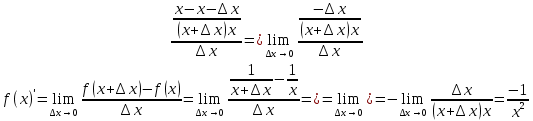 | Тапсырмаларды орындайды. Жауабы : 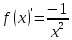 | | Парақша лар | |||||||||
| 5 минут | | Бүгінгі сабақта: - аргумент өсімшесі мен функция өсімшесінің анықтамаларын біледі; - функция туындысының анықтамасын білу және анықтама бойынша функцияның туындысын таба алады. Кері байланыс:
| Тақырыпты меңгергенін анықтау Үйге тапсырма. №39.3. | Кері байланыс | | |||||||||
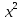 -1; 2) f(х)=
-1; 2) f(х)=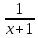 ; 3) f(х)=
; 3) f(х)=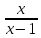 ; 4) f(х)=
; 4) f(х)=