Файл: Лекция течение газа при внешних воздействиях план лекции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ОСНОВЫ ГИДРОДИНАМИКИ (МЖГ и ГГД)
Лекция 7.
ТЕЧЕНИЕ ГАЗА ПРИ ВНЕШНИХ ВОЗДЕЙСТВИЯХ
План лекции
Течение газа в канале переменного сечения. Сопло Лаваля. Течение газа при различных воздействиях.
Конспект лекции
Течение газа в канале переменного сечения.
А) Уравнение Гюгонио
Рассмотрим одномерное течение газа в канале с переменной площадью сечения. Запишем в дифференциальной форме:
- уравнение сплошности
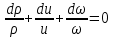 (а)
(а)- уравнение Бернулли
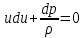 (б)
(б)Учтем, что скорость звука и число Маха, определены соотношениями:
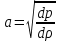 (в)
(в)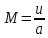 (г)
(г)Из приведенных выражений нетрудно получить
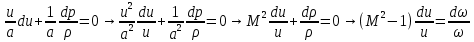
формы уравнения Гюгонио:
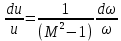 (7.1)
(7.1)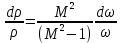 (7.2)
(7.2)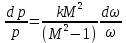 (7.3)
(7.3)Б) Анализ уравнения Гюгонио
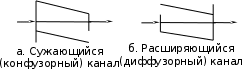
а. Конфузорный канал
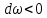 :
:1 – дозвуковой поток
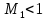 тогда
тогда 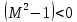 и из (7.1)
и из (7.1) 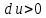 , т.е. скорость возрастает.
, т.е. скорость возрастает. 2 – сверхзвуковой поток
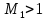 тогда
тогда 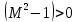 и из (7.1)
и из (7.1) 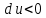 , т.е. скорость падает.
, т.е. скорость падает. б. Диффузорный канал
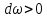 :
:1 – дозвуковой поток
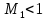
тогда
 и из (7.1)
и из (7.1)  , т.е. скорость падает.
, т.е. скорость падает. 2 – сверхзвуковой поток
 тогда
тогда  и из (7.1)
и из (7.1)  , т.е. скорость возрастает.
, т.е. скорость возрастает. 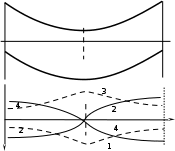 г) Сопло Лаваля
г) Сопло ЛаваляИз (7.1) вытекает, что в трубе типа «диффузор - конфузор» можно получить переход через скорость звука в сечении
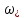 , где
, где 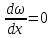
Такое сопло называют сопло Лаваля.
Изменение скорости и числа Маха в нем показано на рис. Б.
Для расчета сопла Лаваля применяют выражения (6.25), которые через приведенные параметры (6.27) и (6.28), записывают в виде
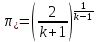 ,
, 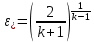 ,
,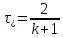 ,
, 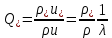 . (6.25)
. (6.25)Последнее соотношение можно представить в виде
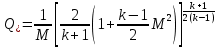 (7.4)
(7.4)Течение газа при различных воздействиях
Помимо изменения площади проходного сечения (геометрическое воздействие) на поток газа оказывают действие и другие явления, например, подвод тепла и работы. В качестве примера приведем эффекты геометрических и тепловых воздействий на поток в форме таблицы.
| Изменение параметра | 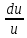 | 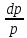 | 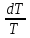 | 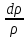 | |
| в о з д е й с т в и е | 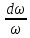 | 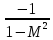 | 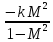 | 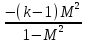 | 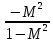 |
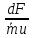 | 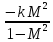 | 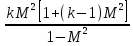 | 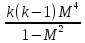 | 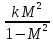 | |
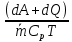 | 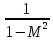 | 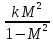 | 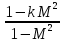 | 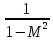 | |
В каждой клетке таблицы стоит коэффициент пропорциональности между воздействием и относительным приращением искомой функции. Например, при подводе тепла Q к газу в трубе постоянного диаметра, используя первый и третий столбцы нижней строки получим
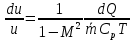 и
и 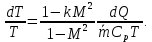
Таким образом, при подводе тепла к дозвуковому потоку
 газ ускоряется и его температура растет, если
газ ускоряется и его температура растет, если 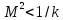 .
. Общей характерной особенностью является обращение знака эффекта при переходе от дозвукового потока к сверхзвуковому, т.к. все коэффициенты содержат в знаменателе множитель
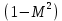 .
.