ВОПРОСЫ К ЭКЗАМЕНУ ЗА 1 СЕМЕСТР Менеджмент 38.03.02

1. 
   Матрицы и их классификации.
   

Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита (А, В, С…), а элементы матриц строчными буквами с двойным индексом: а_ij , где i – номер строки, j – номер столбца.

Матрица размерности m m называется квадратной матрицей порядка m . Матрица, состоящая из элементов одной строки, размерности 1×n, называется матрицей-строкой.

Матрица, состоящая из элементов одного столбца, размерности m×1, называется матрицей-столбцом. . Нулевой матрицей называется матрица, все элементы которой равны нулю, т.е. aij = 0, ∀ i, j.

Диагональ квадратной матрицы, идущая от левого верхнего угла к правому нижнему, называется главной диагональю.

Диагональ идущая от левого нижнего к правому верхнему углу, называется побочной. Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы нули, называется единичной матрицей и обозначается Е

Единичная матрица является диагональной. Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

Две матрицы одной размерности равны друг другу, если равны все элементы этих матриц, стоящие на одинаковых местах

Матрица, полученная из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A T :

2. 
   Матрицы и действия над ними.
   

Элементарными преобразованиями над строками матриц называются следующие преобразования строк:

1. умножение строки на ненулевое число;

2. перестановка двух строк;

3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число;

4. удаление из матрицы или приписывание к матрице ряда, целиком состоящего из нулей;

5. транспонирование матрицы. Если от матрицы A к матрице B можно перейти с помощью элементарных преобразований над строками, то такие матрицы называют эквивалентными и обозначают A

B.

---

3. 
   Ранг матрицы.
   

Определение. Строка называется линейной комбинацией строк матрицы A, если она равна сумме произведений этих строк на произвольные действительные числа .

Определение. Строки (столбцы) матрицы А называются линейно зависимыми, если существует такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке: 6 , (*) . Линейная зависимость строк матрицы означает, что хотя бы 1 строка матрицы является линейной комбинацией остальных.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы, через которые линейно выражаются все остальные строки (столбцы). Теорема. Ранг системы строк матрицы равен её рангу системы столбцов. Рангом матрицы A называется ранг её системы строк или столбцов. Обозначается rang A или r(A) Элементарные преобразования над строками (столбцами) матрицы не меняют её ранга.

Ступенчатой называется матрица, удовлетворяющая следующим условиям:

1) если эта матрица содержит нулевую строку, то все строки, расположенные ниже, также нулевые;

2) если первый ненулевой элемент некоторой строки расположен в столбце с номером k, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем k. Ранг ступенчатой матрицы равен количеству её ненулевых строк.

4. 
   Системы линейных уравнений: основные понятия, формы записи. Основная и расширенная матрицы системы линейных уравнений.
   

Уравнение называется линейным, если неизвестные величины входят в него только в первой степени и не перемножаются друг с другом. Система линейных алгебраических уравнений (СЛАУ) может быть записана в следующем виде:



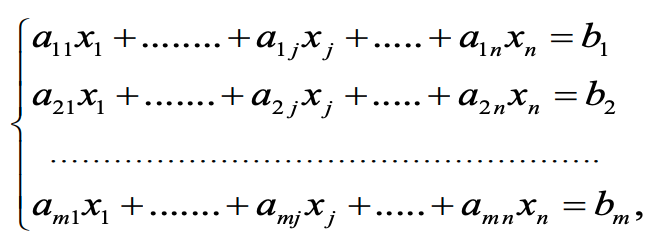
Где Х1,Х2,Х3,…Хn-переменные

a(ij) и b(i) (i=1…m,j=1…n)

СЛАУ называется совместной, если она имеет, хотя бы одно решение. В противном случае система называется несовместной (не имеет ни одного решения)

Совместная система называется определённой, если она имеет единственное решение. Совместная система называется неопределённой если имеет более одного решения. Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

---

5. 
   Теорема Кронекера–Капелли. Исследование системы линейных уравнений.
   

Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы

. Возможны два случая:

1) Система имеет единственное решение, если ранг равен числу неизвестных r = n;

2) Система имеет бесконечное множество решений, если ранг меньше числа неизвестных r < n.

Замечание: r(A) ≤ r(A|B).

6. 
   Метод Гаусса решения систем линейных уравнений.
   

Метод Гаусса - метод последовательного исключения переменных. Метод является одним из наиболее универсальных методов решения СЛАУ. Посредством последовательного исключения неизвестных с помощью элементарных преобразований, система приводится к ступенчатой (в частности, треугольной) системе, равносильной исходной

7. 
   Числовые множества.
   

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются: Множество натуральных чисел N = {1, 2, 3, 4, …}. Сумма и произведение натуральных чисел является натуральным числом. Множество целых чисел Z = {0;1; 2; 3;...}, состоящее из натуральных чисел, числа 0 и чисел, противоположных натуральным числам. Сумма, произведение и разность двух целых чисел является целым числом.

Множество рациональных чисел вида m/n , где m, nZ, n  0. Обозначается это множество буквой Q. Сумма, разность, произведение и частное (если знаменатель не равен нулю) двух рациональных чисел является рациональным числом. Множество действительных (вещественных) чисел, состоящее из рациональных чисел и бесконечных непериодических десятичных дробей, оно обозначается буквой R. Сумма, разность, произведение и частное (если знаменатель не равен нулю) двух действительных чисел является действительным числом

8. 
   Понятие функции.
   

Пусть Х, Y - некоторые множества, элементами которых являются некоторые числа. Если каждому числу по некоторому закону или правилу f ставится в соответствие число то говорят, что на множестве Х задана числовая функция f и записывают y = f (x) . Переменная x называется независимой переменной (аргументом), переменная y - зависимой переменной (от x) или функцией.

---

Пусть х0 - любое действительное число (точка на числовой прямой). Окрестностью точки х0 называется любой интервал (a; b), содержащий точку х0 .

Основные элементарные функции:

1. 
   Постоянная функция
   
2. 
   Корень n-ой степени
   
3. 
   Степенная функция
   
4. 
   Показательная функция
   
5. 
   Логарифмиеская функция
   

9. 
   Предел функции.
   

10. 
    Основные теоремы о пределах функции.
    

11. 
    Непрерывность функции в точке. Непрерывность функции на промежутке. Точки разрыва функции.
    

функция непрерывна в точке , если предел функции в данной точке равен значению функции в этой точке

Функция называется непрерывной на данном промежутке, если она непрерывна в каждой точке этого промежутка. В частности, функция f(x) называется непрерывной на отрезке [????, ????], если она:

1. непрерывна в каждой точке интервала (????, ????),

2. непрерывна справа в точке a,

3. непрерывна слева в точке b.

Точки, в которых нарушается условие непрерывности, называются точками разрыва функции f(x). Точки разрыва подразделяются на точки разрыва первого и второго родов.

Если в точке х0 существуют односторонние пределы lim ????→????0−0 ????(????) = ????1 и lim ????→????0+0 ????(????) = ????2, причем не все три числа f(x0), ????1 и ????2 равны между собой, то х0 называется точкой разрыва первого рода. В частности, если ????1 = ????2, то х0 называется точкой устранимого разрыва. Если ????1 ≠ ????2, х0 называется точкой конечного разрыва. Величина|????1− ????2 | называется скачком функции в точке разрыва первого рода.

Точка х0 называется точкой разрыва второго рода, если по крайней мере один из односторонних пределов функции не существует или равен бесконечности.

12. 
    Производная функции. Теорема о связи дифференцируемости и непрерывности функции. Геометрический, физический и экономический смысл производной.
    

---

Пусть на интервале (a, b) задана функция y = f(x). Возьмем некоторое число x ∈ (a, b)и придадим аргументу x приращение Δx. Тогда значение функции получит приращение

Δy = f(x + Δx) − f(x).



Если при Δx → 0 существует конечный предел дроби dy/dx , то этот Δx предел называют произвoдной функции y = f(x) в точке x и обозначают символом y′(x) или f′(x):



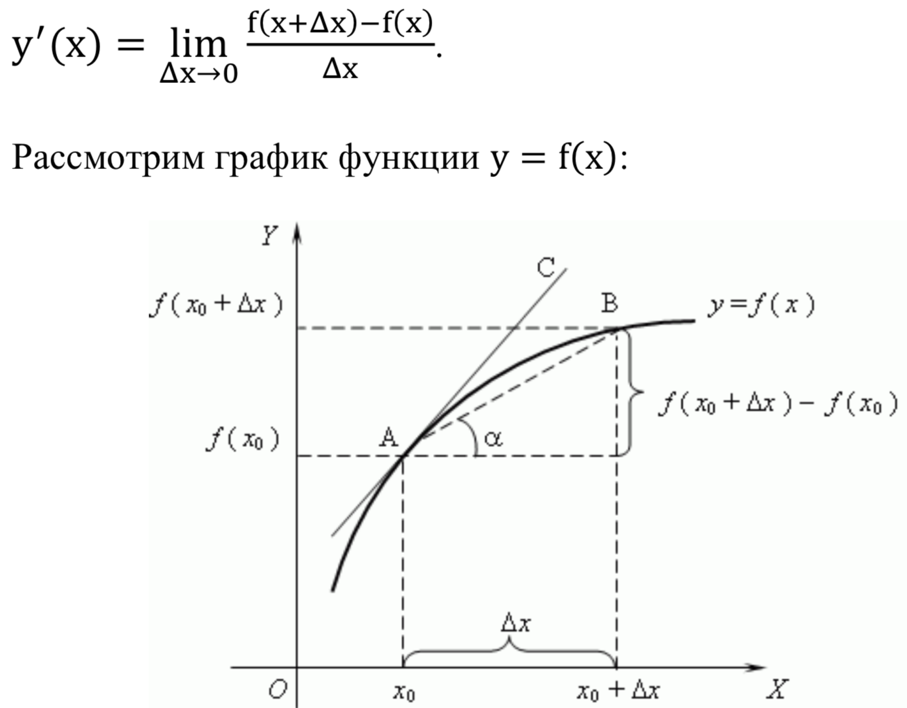
для любых двух точек A и B графика функции:



где ???? - угол наклона секущей ????????.

Если зафиксировать точку A и двигать по направлению к ней точку B, то Δx неограниченно уменьшается и приближается к 0, а секущая AB приближается к касательной AC.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.

Теорема о связи дифференцируемости и непрерывности функции.

Теорема. Если функция    дифференцируема в некоторой точке  a, то она непрерывна в этой точке.
Доказательство. По определению производной



Экономический смысл производной.
Производная выступает как интенсивность изменения некоторого экономического обьекта (процесса) по времени или относительно другого исследуемого фактора.

13. 
    Правила дифференцирования суммы, разности, произведения и частного функций.
    

Нахождение производной называют дифференцированием функции.

Функцию f(x) называют дифференцируемой в точке ????, если в окрестности этой точки ее приращение может быть представлено в виде:

∆y = A ∙ Δx + ο(Δx).
A — число, не зависящее от Δх

ο(Δx) имеет более высокий порядок малости относительно Δx при Δх → 0.

14. 
    Дифференциал функции, его геометрический смысл.
    

Выражение Ax = y(x)x называют

---

Смотрите также файлы

• Цель занятия формирование умений решать текстовые задачи применять математические методы для решения профессиональных задач закрепление навыков решения простейших статистических задач.docx

• Контрольная работа по мдк. 03. 01. Особенности конструкций автотранспортных средств для специальности 23. 02. 07 Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей.docx

• Удк 349. 232 Горбатов Иван Владимирович.pdf

• Контрольная работа по дисциплине Психология Тема 17. Структура характера. Формирование характера.docx

• Дисциплина Основы научной деятельности исследований.docx