Файл: Вопросы к экзамену за 1 семестр менеджмент 38. 03. 02.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 30
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
дифференциалом функции и обозначают dy . Приращение аргумента x называют дифференциалом независимой переменной и обозначают
dx (dxx).Таким образом, dy=y(x)dx.
Геометрически дифференциал dy есть приращение ординаты касательной S, проведенной к графику функции в точке ????(????,????), при изменении x (аргумента) на величину Δ???? = ????????.Дифференциал может быть как меньше, так и больше приращения функции y . Для линейной функции
y = k x + b y = dy.
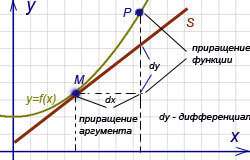
Дифференциалом функции ???????? = ????′???????? в некоторой точке x называется главная, линейная относительно Δ????, часть приращения функции.
Чем меньше Δ????, тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки Р к оси OX, ближе к началу координат.
Поэтому при малых значениях Δ???? (и при ????′ ≠ 0) приращение функции можно приближённо заменить его главной частью ????′Δ????, то есть Δ???? ≈ ????′Δ????.
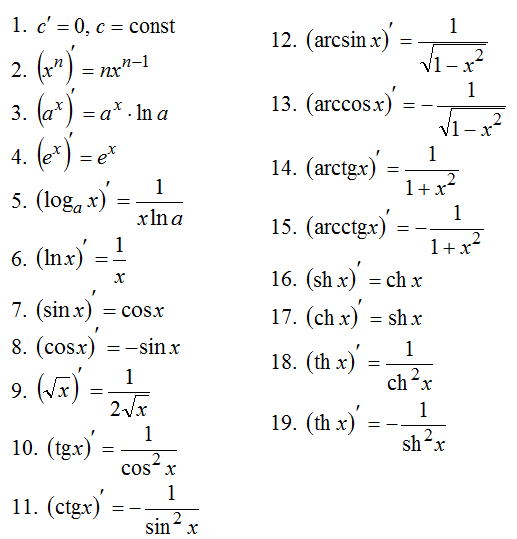
Производные высших порядков.
Пусть функция y=f(x) дифференцируемая на некотором промежутке.Производная у'=f'(х) называется производной 1-го порядка и представляет собой так же функцию от х.
Производная от производной 1-го порядка – называется производной 2-го порядка от функции у=f(x) и обозначается у'', илиf''(х), илиd²y/dx², (d/dx)*(dy/dx),dy'/dx. Таким образом, у''=(у')'. Аналогично от производной 2-го порядка, если она существует, называется производной третьего порядка от функции у=f(x). Обобщив скажем, что производнаяn-го порядка от заданной функции у=f(х), если она существует, называется производной от производной (n-1)-го порядка. Производные выше 1-го порядка называются производными высших порядков.
Дифференциалы высших порядков.
Пусть функция у=f(x) –дифференцируемая функция, а ее аргумент х – независимая переменная. Согласно определению дифференциала функции(dy=f'(х)*dx), есть так же функция от х, можно найти дифференциал от этой функции.
Определение: Дифференциал от дифференциала dy называется дифференциалом второго порядка функции у=f(x) и обозначается(d²y). Таким образом, по определению имеем d²y=d(dy)=(dy')*dx=(f ’(x)*dx)'*dx=f''(x)*(dx)².
Пусть функция y=f(x) определена на интервале (a,b).
Функция f(x) называется неубывающей на данном интервале, если для любых точек x1,x2∈(a,b), таких, что x1, выполняется неравенство f(x1)≤ f(x2).
Если данное неравенство является строгим, т.е. f(x1), то f(x) называется возрастающей на (a,b).
Аналогично определяется невозрастающая функция: если∀ x1,x2∈ (a,b): x1⇒ f(x1) ≥ f(x2);
Для убывающей функции:∀ x1,x2∈(a,b): x1⇒f(x1)>f(x2).
Если функция f(x) определена на интервале (a,b) и принадлежит к одному из рассмотренных типов, то она является монотонной на интервале (a,b).
Достаточное условие возрастания функции. Если производная дифференцируемой функции f(x) положительна внутри некоторого интервала (a,b), то функция f(x) возрастает на этом интервале.
Необходимое условие возрастания функции Если функция f(x) возрастает на интервале (a,b), то f ′(x) ≥ 0, ∀ x∈(a,b).
Достаточное условие убывания функции. Если производная дифференцируемой функции f(x) отрицательна внутри некоторого интервала (a,b), то функция f(x) убывает на этом интервале.
Необходимое условие убывания функции. Если функция f(x) убывает на интервале (a,b), то f ′(x) ≤ 0, ∀ x∈(a,b).
Промежутки, в которых функция возрастает (убывает) называются промежутками монотонности функции.
Замечание. Если функция определена и непрерывна на концах интервала возрастания или убывания (a;b), то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке.
Точки, в которых производная функции равна нулю, называются стационарными точками.
Точки, в которых производная функции равна нулю либо не существует, называются критическими точками.
Необходимое условие локального экстремума.
Функция f(x) имеет локальный максимум в точке x0, если в некоторой окрестности точки x0, выполняется неравенство ????(????0) ≥ ????(????).
Функция f(x) имеет локальный минимум в точке x0, если в некоторой окрестности точки x0, выполняется неравенство ????(????0) ≤ ????(????).
 Точки локального максимума и локального минимума называют точками локального экстремума.
Точки локального максимума и локального минимума называют точками локального экстремума.
Необходимое условие экстремума
Если точка является точкой экстремума функции , то в этой точке либо производная равна нулю, либо не существует.
Экстремумы функции содержатся среди критических точек функции (точки, в которых производная функции равна нулю или не существует).

Пусть функция f(x) дифференцируема в любой точке промежутка (a;b), тогда существует касательная к графику
функции y=f(x), проходящая через любую точку М(x, f(x)) этого графика (a, причем эта касательная не параллельна оси OY.
График функции y=f(x) является выпуклым вверх (выпуклым) в промежутке (a;b), если в пределах данного промежутка он лежит не выше любой своей касательной.
График функции y=f(x) является выпуклым вниз (вогнутым) в промежутке (b;c), если в пределах данного промежутка он лежит не ниже любой своей касательной.
Точка графика функции, отделяющая части графика, выпуклые в разных направлениях, называется точкой перегиба графика функции.
В точке перегиба касательная пересекает график функции.
Если во всех точках промежутка (a;b) вторая производная функции f(x) отрицательна (f"(????)<0), то график функции y=f(x) является выпуклым вверх ( выпуклым) в промежутке (a;b).
Если во всех точках промежутка (b;c) вторая производная функции f(x) положительна (????"(????) > 0), то график функции y=f(x) является выпуклым вниз ( вогнутым) в промежутке (b;с).
Прямая линия называется асимптотой графика функции, если расстояние от точки М, лежащей на кривой, до этой прямой, стремится к нулю при неограниченном удалении точки от начала координат.
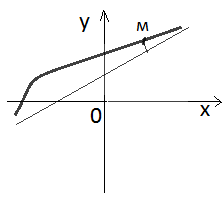
Прямая x=x0 является вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений
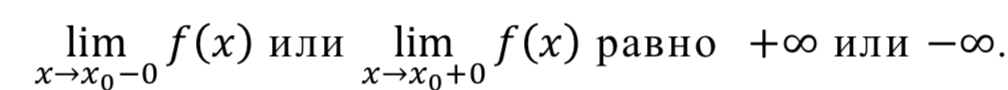

Первообразной для функции f(x) на некотором промежутке, называется функция F(x) , если для всех значений х из этого промежутка выполняется равенство F(x)= f(x) илиdF(x)= f(x)dx.
Неопределенным интегралом от функции f (x) называется совокупность всех первообразных F(x)+C , где F(x) – первообразная для функции f (x) , С – произвольная постоянная. Неопределенный интеграл обозначается символом f (x)dx.
Таким образом, f (x)dx=F(x)+C .
Интегрированием функции f (x) называется операция нахождения неопределенного интеграла от данной функции. Операция
интегрирования является обратной к операции дифференцирования.
Свойства неопределенного интеграла
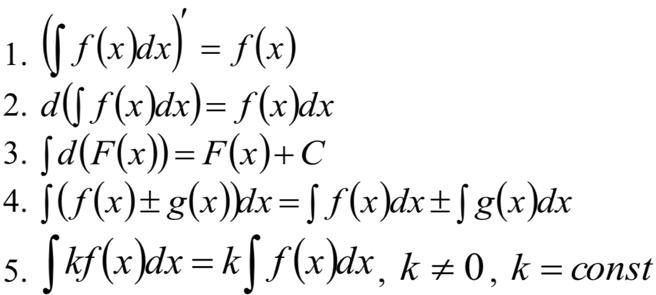
24.Таблица неопределенных интегралов.
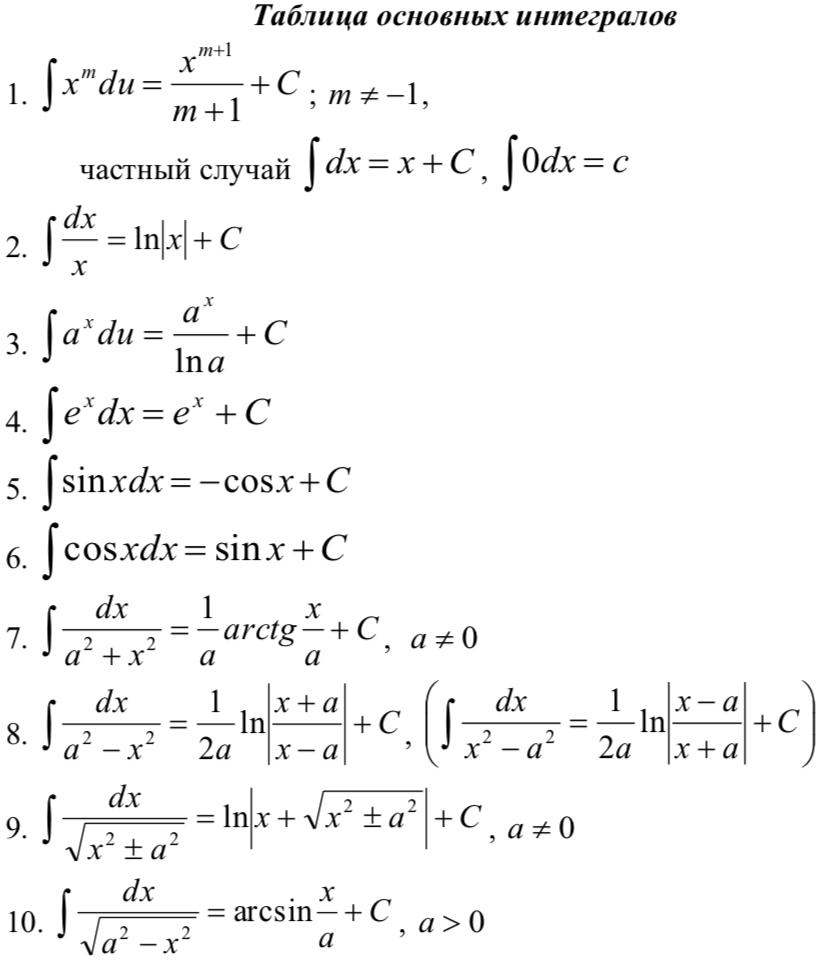
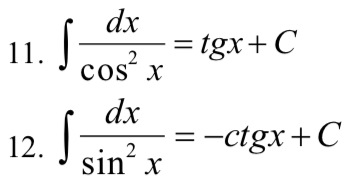
25.Основные методы интегрирования. Табличное интегрирование.
Непосредственное интегрирование
Непосредственным интегрированием называется вычисление интегралов с использованием таблицы основных неопределенных интегралов, их свойств, а также тождественных преобразований подынтегрального выражения.
26.Замена переменной в неопределенном интеграле.
Замена переменной под знаком неопределенного интеграла.
Замена переменной под знаком неопределенного интеграла производится с помощью подстановок двух видов. Рассмотрим эти подстановки.
Формула замены переменной
Пусть x =(t), где функция (t) определена и дифференцируема.
Тогда формула замены переменной имеет вид:
f (x)dx= f ((t))(t)dt.
27.Интегрирование по частям в неопределенном интеграле.
Теорема. Если u(x) и v(x) – функции переменной интегрирования,
То справедлива формула udv=uv−vdu,
которая называется формулой интегрирования по частям. Она используется в случаях, когда вычисление интеграла vdu оказывается
более простым, чем вычисление исходного интеграла udv .
Метод интегрирования по частям применяется при вычислении следующих интегралов:
a)P (x)eax+bdx, P (x)sin(ax+b)dx, P (x)cos(ax+b)dx, где P (x)– nnnn
многочлен степени n. В данных интегралах за u(x) принимается Pn (x) и интегрируется по частям n раз.
b)Pn(x)lnx dx, Pn(x)arcsinxdx, Pn(x)arccosxdx, Pn(x)arctgxdx, Pn(x)arcctgxdx.В данных интегралахза dv принимается Pn(x)dx.
28.Определенный интеграл. Площадь криволинейной трапеции.

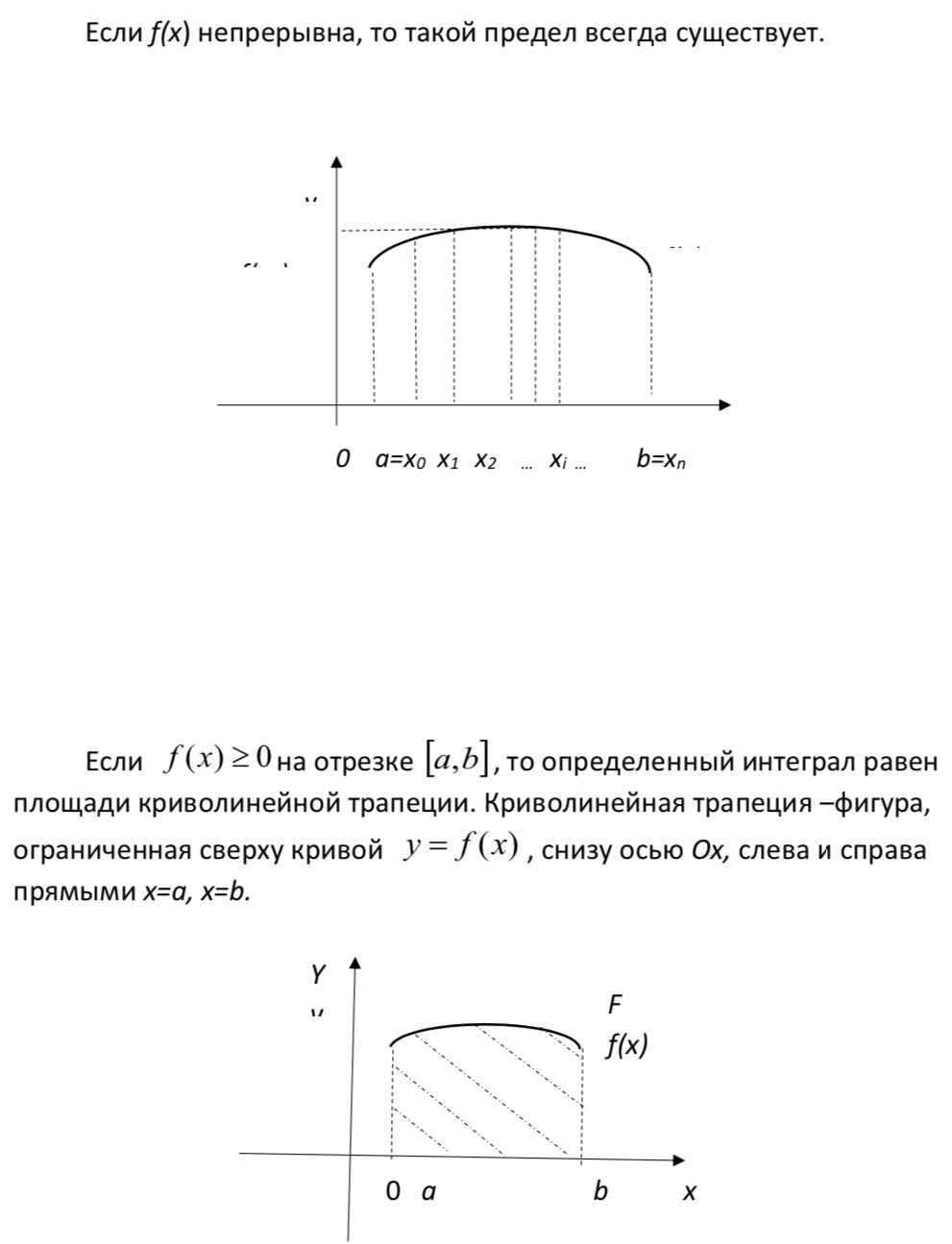
29.Свойства определенного интеграла.


Формула Ньютона-Лейбница
Если функция f(x) интегрируема на отрезке [a, b] и имеет на
нем первообразную, то для любой ее первообразной F(x) на этом
отрезке справедлива формула:
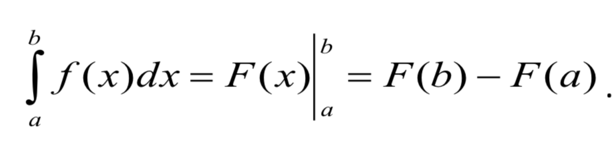
31.Формулы замены переменной и интегрирования по частям в определенном интеграле.
Интегрирование по частям в определенном интеграле
Если функции u(x) и v(x) дифференцируемы на a,b, то справедлива формула:
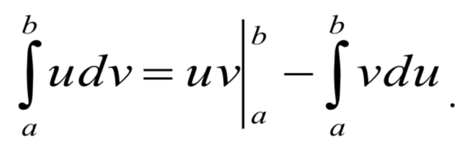

32. Вычисление площади с помощью определенного интеграла.

dx (dxx).Таким образом, dy=y(x)dx.
Геометрически дифференциал dy есть приращение ординаты касательной S, проведенной к графику функции в точке ????(????,????), при изменении x (аргумента) на величину Δ???? = ????????.Дифференциал может быть как меньше, так и больше приращения функции y . Для линейной функции
y = k x + b y = dy.

Дифференциалом функции ???????? = ????′???????? в некоторой точке x называется главная, линейная относительно Δ????, часть приращения функции.
Чем меньше Δ????, тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки Р к оси OX, ближе к началу координат.
Поэтому при малых значениях Δ???? (и при ????′ ≠ 0) приращение функции можно приближённо заменить его главной частью ????′Δ????, то есть Δ???? ≈ ????′Δ????.
-
Таблица производных основных элементарных функций.
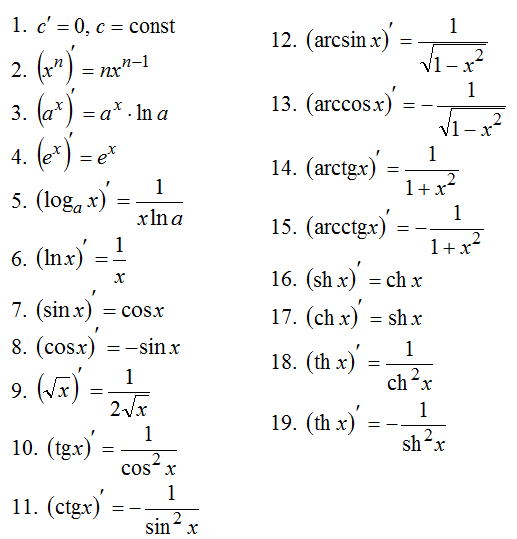
-
Производные и дифференциалы высших порядков.
Производные высших порядков.
Пусть функция y=f(x) дифференцируемая на некотором промежутке.Производная у'=f'(х) называется производной 1-го порядка и представляет собой так же функцию от х.
Производная от производной 1-го порядка – называется производной 2-го порядка от функции у=f(x) и обозначается у'', илиf''(х), илиd²y/dx², (d/dx)*(dy/dx),dy'/dx. Таким образом, у''=(у')'. Аналогично от производной 2-го порядка, если она существует, называется производной третьего порядка от функции у=f(x). Обобщив скажем, что производнаяn-го порядка от заданной функции у=f(х), если она существует, называется производной от производной (n-1)-го порядка. Производные выше 1-го порядка называются производными высших порядков.
Дифференциалы высших порядков.
Пусть функция у=f(x) –дифференцируемая функция, а ее аргумент х – независимая переменная. Согласно определению дифференциала функции(dy=f'(х)*dx), есть так же функция от х, можно найти дифференциал от этой функции.
Определение: Дифференциал от дифференциала dy называется дифференциалом второго порядка функции у=f(x) и обозначается(d²y). Таким образом, по определению имеем d²y=d(dy)=(dy')*dx=(f ’(x)*dx)'*dx=f''(x)*(dx)².
-
Определение и признаки монотонности функции одной переменной.
Пусть функция y=f(x) определена на интервале (a,b).
Функция f(x) называется неубывающей на данном интервале, если для любых точек x1,x2∈(a,b), таких, что x1
Если данное неравенство является строгим, т.е. f(x1)
Аналогично определяется невозрастающая функция: если∀ x1,x2∈ (a,b): x1
Для убывающей функции:∀ x1,x2∈(a,b): x1
Если функция f(x) определена на интервале (a,b) и принадлежит к одному из рассмотренных типов, то она является монотонной на интервале (a,b).
Достаточное условие возрастания функции. Если производная дифференцируемой функции f(x) положительна внутри некоторого интервала (a,b), то функция f(x) возрастает на этом интервале.
Необходимое условие возрастания функции Если функция f(x) возрастает на интервале (a,b), то f ′(x) ≥ 0, ∀ x∈(a,b).
Достаточное условие убывания функции. Если производная дифференцируемой функции f(x) отрицательна внутри некоторого интервала (a,b), то функция f(x) убывает на этом интервале.
Необходимое условие убывания функции. Если функция f(x) убывает на интервале (a,b), то f ′(x) ≤ 0, ∀ x∈(a,b).
Промежутки, в которых функция возрастает (убывает) называются промежутками монотонности функции.
Замечание. Если функция определена и непрерывна на концах интервала возрастания или убывания (a;b), то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке.
Точки, в которых производная функции равна нулю, называются стационарными точками.
Точки, в которых производная функции равна нулю либо не существует, называются критическими точками.
-
Определение локальных экстремумов функции одной переменной.
Необходимое условие локального экстремума.
Функция f(x) имеет локальный максимум в точке x0, если в некоторой окрестности точки x0, выполняется неравенство ????(????0) ≥ ????(????).
Функция f(x) имеет локальный минимум в точке x0, если в некоторой окрестности точки x0, выполняется неравенство ????(????0) ≤ ????(????).
Необходимое условие экстремума
Если точка является точкой экстремума функции , то в этой точке либо производная равна нулю, либо не существует.
Экстремумы функции содержатся среди критических точек функции (точки, в которых производная функции равна нулю или не существует).
-
Определение локальных экстремумов функции одной переменной. Достаточные условия локального экстремума.

-
Определение и признаки выпуклости функции, точки перегиба графика функции.
Пусть функция f(x) дифференцируема в любой точке промежутка (a;b), тогда существует касательная к графику
функции y=f(x), проходящая через любую точку М(x, f(x)) этого графика (a
График функции y=f(x) является выпуклым вверх (выпуклым) в промежутке (a;b), если в пределах данного промежутка он лежит не выше любой своей касательной.
График функции y=f(x) является выпуклым вниз (вогнутым) в промежутке (b;c), если в пределах данного промежутка он лежит не ниже любой своей касательной.
Точка графика функции, отделяющая части графика, выпуклые в разных направлениях, называется точкой перегиба графика функции.
В точке перегиба касательная пересекает график функции.
Если во всех точках промежутка (a;b) вторая производная функции f(x) отрицательна (f"(????)<0), то график функции y=f(x) является выпуклым вверх ( выпуклым) в промежутке (a;b).
Если во всех точках промежутка (b;c) вторая производная функции f(x) положительна (????"(????) > 0), то график функции y=f(x) является выпуклым вниз ( вогнутым) в промежутке (b;с).
-
Асимптоты графика функции.
Прямая линия называется асимптотой графика функции, если расстояние от точки М, лежащей на кривой, до этой прямой, стремится к нулю при неограниченном удалении точки от начала координат.

Прямая x=x0 является вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений

-
Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла.
Первообразной для функции f(x) на некотором промежутке, называется функция F(x) , если для всех значений х из этого промежутка выполняется равенство F(x)= f(x) илиdF(x)= f(x)dx.
Неопределенным интегралом от функции f (x) называется совокупность всех первообразных F(x)+C , где F(x) – первообразная для функции f (x) , С – произвольная постоянная. Неопределенный интеграл обозначается символом f (x)dx.
Таким образом, f (x)dx=F(x)+C .
Интегрированием функции f (x) называется операция нахождения неопределенного интеграла от данной функции. Операция
интегрирования является обратной к операции дифференцирования.
Свойства неопределенного интеграла
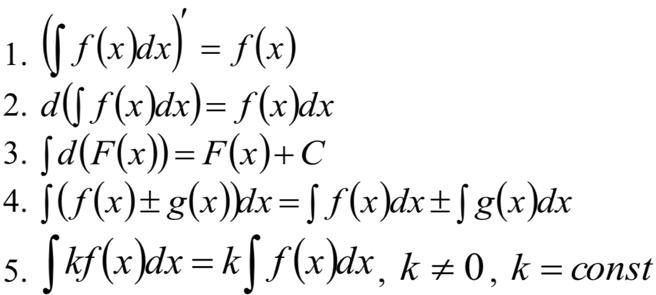
24.Таблица неопределенных интегралов.
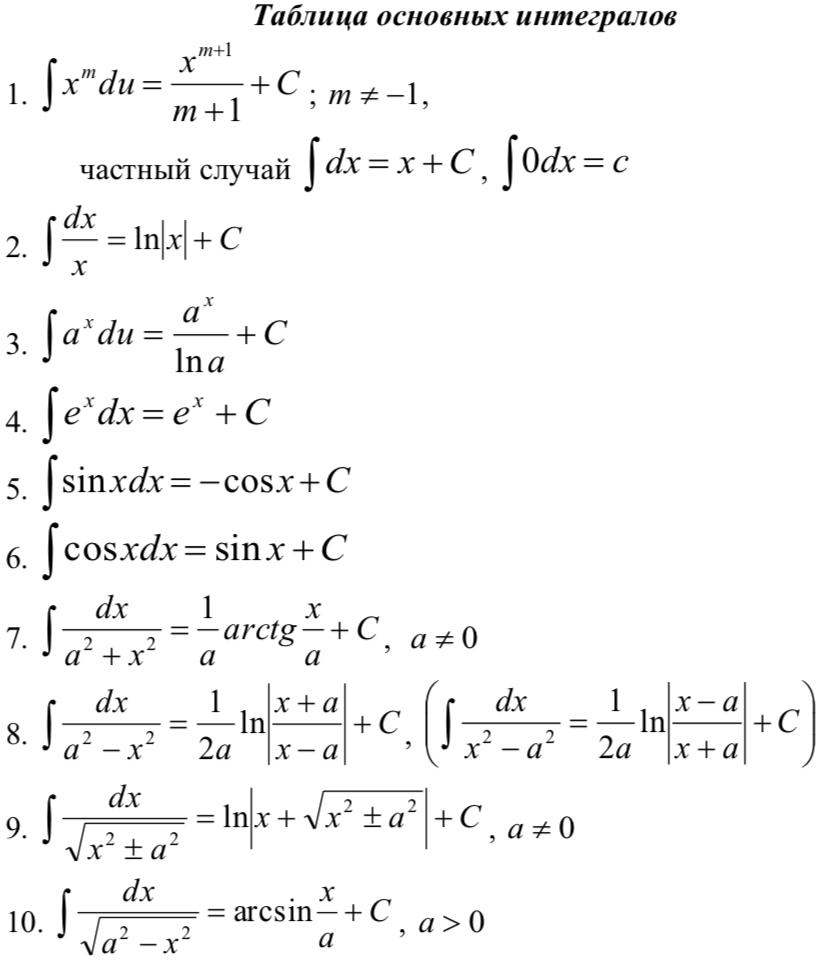
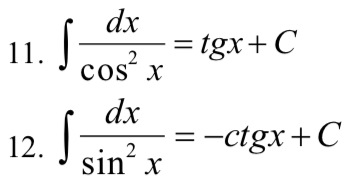
25.Основные методы интегрирования. Табличное интегрирование.
Непосредственное интегрирование
Непосредственным интегрированием называется вычисление интегралов с использованием таблицы основных неопределенных интегралов, их свойств, а также тождественных преобразований подынтегрального выражения.
26.Замена переменной в неопределенном интеграле.
Замена переменной под знаком неопределенного интеграла.
Замена переменной под знаком неопределенного интеграла производится с помощью подстановок двух видов. Рассмотрим эти подстановки.

Формула замены переменной
Пусть x =(t), где функция (t) определена и дифференцируема.
Тогда формула замены переменной имеет вид:
f (x)dx= f ((t))(t)dt.
27.Интегрирование по частям в неопределенном интеграле.
Теорема. Если u(x) и v(x) – функции переменной интегрирования,
То справедлива формула udv=uv−vdu,
которая называется формулой интегрирования по частям. Она используется в случаях, когда вычисление интеграла vdu оказывается
более простым, чем вычисление исходного интеграла udv .
Метод интегрирования по частям применяется при вычислении следующих интегралов:
a)P (x)eax+bdx, P (x)sin(ax+b)dx, P (x)cos(ax+b)dx, где P (x)– nnnn
многочлен степени n. В данных интегралах за u(x) принимается Pn (x) и интегрируется по частям n раз.
b)Pn(x)lnx dx, Pn(x)arcsinxdx, Pn(x)arccosxdx, Pn(x)arctgxdx, Pn(x)arcctgxdx.В данных интегралахза dv принимается Pn(x)dx.
28.Определенный интеграл. Площадь криволинейной трапеции.


29.Свойства определенного интеграла.


-
Формула Ньютона-Лейбница.
Формула Ньютона-Лейбница
Если функция f(x) интегрируема на отрезке [a, b] и имеет на
нем первообразную, то для любой ее первообразной F(x) на этом
отрезке справедлива формула:
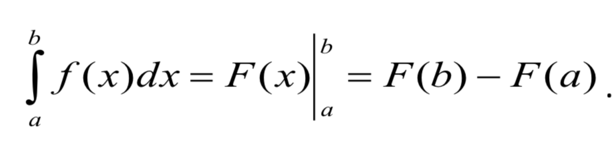
31.Формулы замены переменной и интегрирования по частям в определенном интеграле.
Интегрирование по частям в определенном интеграле
Если функции u(x) и v(x) дифференцируемы на a,b, то справедлива формула:
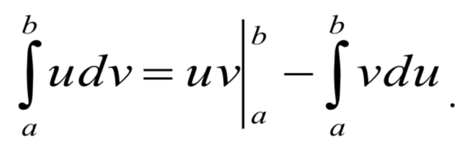

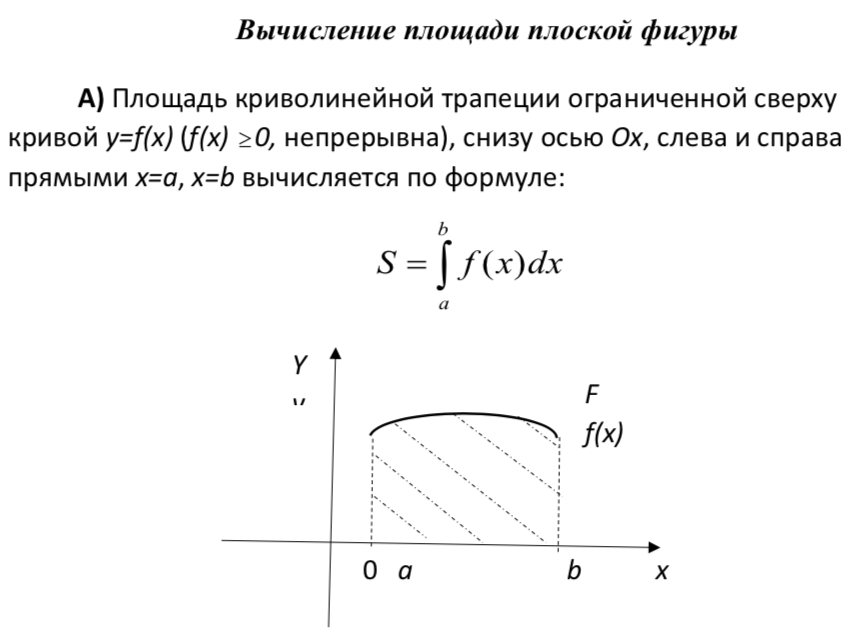
32. Вычисление площади с помощью определенного интеграла.

