Файл: Тело, ограниченное конической поверхностью, точкой и кругом.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Конус– тело, ограниченное конической поверхностью, точкой и кругом.
Коническая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, и точку, не лежащую в плоскости этой окружности.
Пу
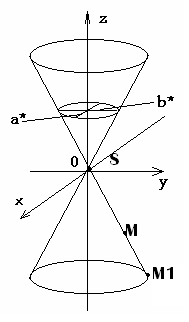 сть задана каноническая поверхность с вершиной в центе координат и плоскости z=h. Пусть она задана в этой плоскости уравнением:
сть задана каноническая поверхность с вершиной в центе координат и плоскости z=h. Пусть она задана в этой плоскости уравнением:z
Пу
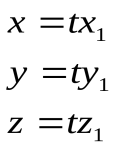 т.к.
т.к. 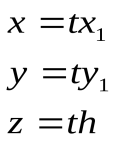
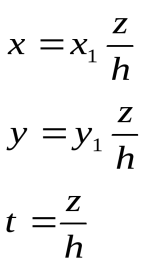
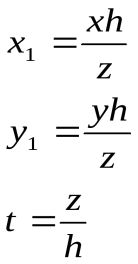 .
.Основные элементы конуса
-
R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB. -
h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD. -
Точка C – вершина конуса. -
l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания. -
Осевое сечение конуса – это равнобедренный треугольник ABC, который образуется в результате пересечения конуса плоскостью проходящей через его ось. -
Поверхность конуса – состоит из его боковой поверхности и основания. Формулы для расчета площади поверхности, а также объема прямого кругового конуса представлены в отдельных публикациях.
Площадь боковой поверхности конуса можно вычислить по следующим формулам:
,
где
Площадь полной поверхности конуса равна сумме площади боковой поверхности конуса и площади его основания.
Тогда площадь полной поверхности конуса можно вычислить по формуле^
где
– его образующая.
Объем конуса можно рассчитать по данной формуле
V=31πr2h