Файл: Отчет по работе "Расчёт термодинамических функций по результатам измерений теплоёмкости методом адиабатической вакуумной калориметрии".docx
Добавлен: 07.12.2023
Просмотров: 53
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Отчет по работе “Расчёт термодинамических функций по результатам измерений теплоёмкости методом адиабатической вакуумной калориметрии”
Цель работы – рассчитать стандартные термодинамические функции меди по результатам измерений теплоёмкости методом адиабатической калориметрии.
Результаты расчетов
-
Получение набора значений мольной теплоёмкости при различных температурах из первичных экспериментальных данных.
В работе были использованы результаты измерения теплоёмкости селенида галлия в интервале температур от 14,51 до 308,26 К. Рассчитанные значения мольной теплоёмкости приведены в таблице 1.
Таблица 1. Результаты расчёта мольной теплоёмкости для Ga2Se3
| T, K | Cp, кДж*моль-1*К-1 | T, K | Cp, кДж*моль-1*К-1 | T, K | Cp, кДж*моль-1*К-1 | T, K | Cp, кДж*моль-1*К-1 |
| 14,51 | 3,3082538283 | 70,3 | 60,0002001292 | 126,31 | 92,8577741146 | 210,99 | 112,470212 |
| 15,66 | 4,3104057848 | 72,78 | 61,9508414549 | 128,89 | 94,2706816705 | 215,08 | 112,7575963 |
| 17,09 | 5,5708864990 | 75,52 | 64,1979313710 | 134,32 | 96,1592994215 | 219,32 | 113,5784051 |
| 19,19 | 8,2910232576 | 78,26 | 65,7376541725 | 136,61 | 96,5584163803 | 224,01 | 114,3297124 |
| 24,58 | 14,4520815454 | 81,65 | 68,5295729792 | 138,93 | 97,5593483039 | 233,47 | 115,299573 |
| 27 | 17,2688909513 | 83,54 | 70,1584391737 | 141,45 | 98,2207945004 | 237,51 | 115,6609317 |
| 29,25 | 19,7282096413 | 85,37 | 71,4120162641 | 145,09 | 99,4295960663 | 241,5 | 116,1121101 |
| 31,69 | 22,6398421651 | 87,12 | 72,5383406395 | 147,9 | 99,8399052060 | 245,71 | 116,3990701 |
| 37,07 | 28,7013496453 | 91,39 | 75,0415148210 | 149,18 | 100,4183192055 | 250,18 | 116,9787946 |
| 41,54 | 32,9478634378 | 93,77 | 76,5915232378 | 153,88 | 101,8679709343 | 259,14 | 117,7498629 |
| 42,97 | 34,5184124710 | 96,39 | 78,3223938104 | 161,64 | 104,1695829318 | 264,13 | 117,9209911 |
| 45,29 | 37,1784967394 | 99,05 | 79,9085615901 | 165,21 | 105,0411355030 | 267,2 | 118,5286009 |
| 50,27 | 41,7379745455 | 101,71 | 81,4686421120 | 168,97 | 105,2414957148 | 272,11 | 118,8277855 |
| 53,04 | 44,3305033815 | 105,01 | 83,5309837587 | 172,77 | 106,1204340046 | 277,07 | 119,4694195 |
| 55,21 | 46,8796058983 | 107,04 | 84,3117306595 | 180,64 | 107,5714736599 | 282,08 | 119,949369 |
| 57,11 | 48,8310434547 | 108,62 | 85,1485581966 | 184,59 | 108,6391567239 | 286,65 | 120,3195425 |
| 60,87 | 51,9318223025 | 112,04 | 86,7107914872 | 188,48 | 109,0292094931 | 290,93 | 120,6091208 |
| 62,69 | 53,6694671475 | 116,11 | 88,9519793679 | 192,77 | 109,9585122386 | 299,22 | 120,9483859 |
| 64,49 | 55,0082088167 | 121,37 | 91,2305454545 | 197,58 | 110,8089760287 | 303,5 | 121,1106672 |
| 66,33 | 56,7996344774 | 123,84 | 91,9492450439 | 206,88 | 111,7389824480 | 308,26 | 121,401878 |
-
Экстраполяция к 0 К экспериментально измеренных значений теплоёмкости
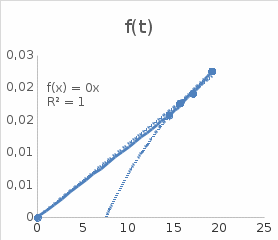
Зависимость Cp(T)/ T2 f(T) , тангенс угла наклона которой соответствует коэффициенту зависимости Cp T3, 9,73*104 Дж/(моль·К4).
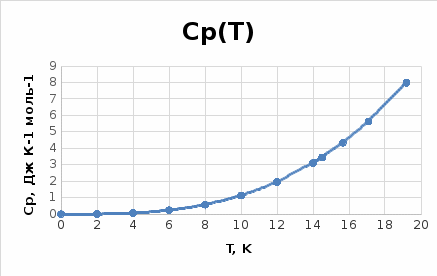
Зависимость теплоёмкости от температуры: точки – эксперимент, линия – расчёт по уравнению Cp T3.
-
Аналитическое интегрирование теоретических зависимостей Cp(T) f(T) и Cp(T)/T f(T), полученных экстраполяцией к 0 К, в интервале от 0 К до Tn.
Таблица 2. Рассчитанные значения Cp , STo и [HTo H0o] при низких температурах
| T, K | Cp, кДж*моль-1*К-1 | ST0, Дж*моль-1*К-1 | [HT0-H00], Дж*моль-1 |
| 0 | 0 | 0 | 0 |
| 2 | 0,00904 | 0,003013333 | 0,00452 |
| 4 | 0,07232 | 0,024106667 | 0,07232 |
| 6 | 0,24408 | 0,08136 | 0,36612 |
| 8 | 0,57856 | 0,192853333 | 1,15712 |
| 10 | 1,13 | 0,376666667 | 2,825 |
| 12 | 1,95264 | 0,65088 | 5,85792 |
| 14 | 3,10072 | 1,033573333 | 10,85252 |
-
Численное интегрирование первичных экспериментальных данных в координатах Cp(T) f(T) и Cp(T)/T f(T).
Таблица 3. Стандартные термодинамические функции вещества (Ga2Se3), полученные с помощью численного интегрирования
| Расчет | Литературные данные при 298,15 К | ||
| S0299,22, Дж*моль-1*К-1 | [H0299,22-H00], Дж*моль-1 | S0298,15, Дж*моль-1*К-1 | [H0298,15-H00], Дж*моль-1 |
| 180,86 | 25452,62 | 180,4 | 25320 |
-
Аппроксимация экспериментальных данных с помощью комбинации функций Планка−Эйнштейна.
Таблица 4. Параметры функций Планка−Эйнштейна
| N | αi | θi, K |
| 1 | 1,59 ± 0,03 | 193,1 ± 10,7 |
| 2 | 0,48 ± 0,03 | 1591,4 ± 157 |
| 3 | 1,37 ± 0,02 | 86,0 ± 7,4 |
| 4 | 2,13 ± 0,04 | 369,2 ± 48 |
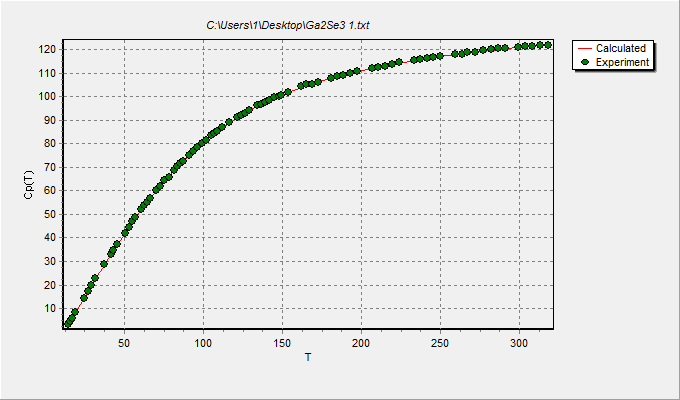
График зависимости Cp(T) (в Дж·К–1 ·моль–1) от температуры (в К) для селенида галлия: точки – экспериментальные значения, линия – расчёт с использованием функций Планка−Эйнштейна
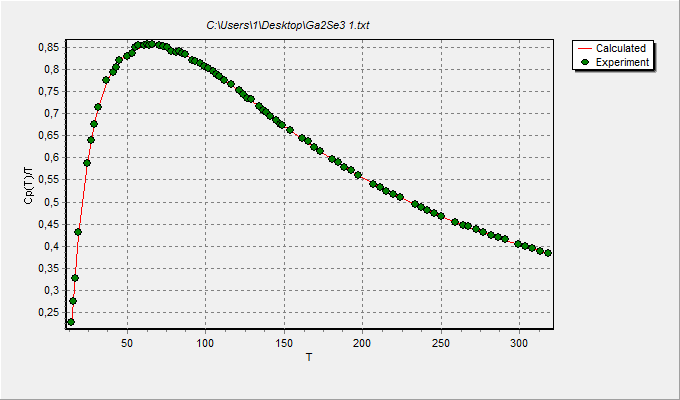
График зависимости Cp(T)/T (в Дж·К–2 ·моль–1) от температуры (в К) для селенида галлия: точки – экспериментальные значения, линия – расчёт с использованием функций Планка−Эйнштейна
-
Расчёт сглаженных значений термодинамических свойств изучаемого соединения
Таблица 5. Стандартные термодинамические функции вещества (Ga
2Se3), полученные при использовании функций Планка−Эйнштейна
| Т, K | Cp, кДж*моль-1*К-1 | S0T, Дж*моль-1*К-1 | [H0T-H00], Дж*моль-1 |
| 0 | 0 | 0 | 0 |
| 50 | 41,70753394 | 24,0297896 | 819,5354401 |
| 100 | 80,52260197 | 66,01854241 | 3961,148875 |
| 200 | 111,0041919 | 133,5321234 | 13875,09491 |
| 298 | 120,7963228 | 179,8746885 | 25295,42429 |
| 300 | 120,9329252 | 180,6831509 | 25537,1538 |
| 400 | 126,2352376 | 216,2617127 | 37917,14703 |
| 500 | 129,6285762 | 244,8207134 | 50721,93688 |
Ответы на вопросы.
1. Приведите определение теплоёмкости. От каких факторов она зависит? Какова её размерность?
Теплоемкость - коэффициент пропорциональности между количеством поглощённой теплоты Q и повышением температуры dT: Cx = (Q/ dT)x, где x обозначает конкретные условия, при которых проводится эксперимент (например, постоянство p, V и т.д.). Значение теплоемкости зависит от условий теплообмена. Теплоёмкость имеет размерность Дж·К−1 (или кал·К−1 ). Обычно величину теплоёмкости относят к определённой массе или количеству вещества: грамму или 4 молю. Поэтому удельная теплоёмкость имеет размерность Дж·К−1 ·г −1 , а мольная Дж·К−1 ·моль−1 .
2. Что такое теплоёмкости C
V и Cp? Изохорную или изобарную теплоёмкость измеряют в ходе рассмотренного опыта? Как рассчитать разность CVCp? Приведите все известные Вам соотношения (в общем случае, для идеального газа, для твёрдых тел).
Поскольку теплота не является свойством системы, а Q − полным дифференциалом, то теплоёмкость в общем случае в соответствии с её определением также не является свойством системы, а её значение зависит от условий теплообмена. Однако, в двух наиболее важных для практики процессах − при постоянном объёме и при постоянном давлении − теплоёмкость приобретает свойства функции состояния, и можно записать равенства: Cv=QV/dT=(U/T)v и Cp= Qp/dT (H/T)p, где CV и Cp − теплоёмкости соответственно при постоянном объёме и при постоянном давлении, U − внутренняя энергия, H − энтальпия системы. Величины QV/dT и Qp/dT могут быть определены экспериментально с помощью калориметра. Для решения практических задач в большинстве случаев достаточно знать порядок разности CVCp.
Для идеального газа: CVCp=NR (уравнение Майера)
Для твердого тела: CVCp=0,0214*Cp2*T/Tпл (эмпирическая формула Нернста)
3. За изменением какой величины ведут наблюдение в ходе калориметрического опыта?
За разностью температур между калориметром и оболочкой железо родиевого термометра. Контролируется с помощью четырехспайной дифференциальной термопары (медь-железо)/хромель.
4. Какие способы аппроксимации экспериментальных данных по температурной зависимости теплоёмкости Вам известны? Опишите их.
Результатом измерения теплоёмкости является набор значений Т и Cx (x = p, V). Аппроксимацию экспериментальных данных проводят разными способами: с использованием комбинаций функций Дебая и Эйнштейна, с помощью сплайн-функций, полиномиальных зависимостей и др. Наиболее распространённые полиномиальные зависимости с варьируемыми параметрами ai.
С помощью программы «Cp_approx» можно выполнить аппроксимацию экспериментальных данных. Внеся экспериментальные данные Т и Ср, можно получить график Ср(Т). Расчеты покажут Ср (расчетную), Ср (экспериментальную) и разность между ними. Погрешность аппроксимации можно варьировать с помощью варьирования числа параметров функций Планка-Эйнштейна (коэффициентов аi и Thetta).