1. 
   Задача 2.10
   

Условие:

Квадратное отверстие размером B×B=1×1 м в вертикальной стенке резервуара закрыто плоским поворотным щитом, который прижимается к стенке под действием груза массой m, расположенного на плечеr = 1,5 м.

1. Найти минимальную массу груза m, достаточную для удержания воды в резервуаре на уровне H = 2 м, если расстояние от верхней кромки отверстия до оси вращения щита h = 0,3 м. Определить при этом реакцию R цапф А щита.

2. Определить, какой наименьший вакуум p_в над водой в резервуаре будет удерживать щит без груза.



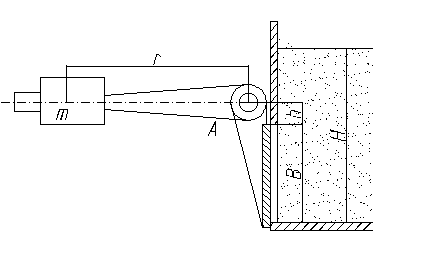
Решение:

1. Решаем задачу в избыточной системе (р_атм=0). «Вложим» ось y в стенку, отметим 0 на пересечении с П.П(пьезометрическая плоскость совпадает с поверхностью жидкости).



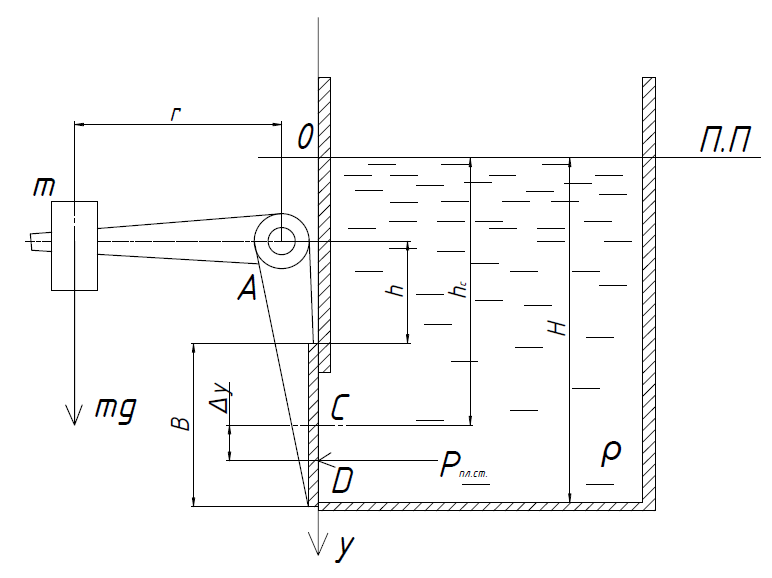
Тогда давление в центре тяжести щита:

р_с = ρ · g·h_c;

где h_c = H – B/2 – заглубление точки С,

ρ = 1000 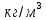- плотность воды.

p_c = 1000 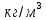· 9,8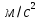 · (2 м — 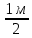)= = 14700 Па

Сила давления на щит:

Р_пл.ст. = р_с · A ; где А = В·В — площадь щита.

Р_пл.ст.=14700 Па · 1 м · 1 м = 14700 Н

Найдем смещение центра давления D относительно центра тяжести щита:

Δy= 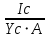; где Y_c – ордината точки С (совпадает с h_c), I_c = 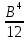- момент инерции квадратного сечения.

Δy = 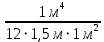≈ 0,0556 м

Так, зная величину и точку приложения Р_пл.ст., мы можем найти массу груза, исходя из того условия, что для равновесия щита необходимо

---

, чтобы сумма моментов сил относительно точки А должна быть равна нулю:

m·g·r – P_пл.ст.·(h + 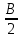+Δy) = 0 =>

m= 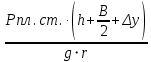= 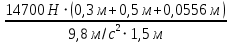≈ 856 кг

Для определения реакции Rцапф А воспользуемся методом РОЗУ.

Отбросим опору в точке А и заменим ее действие вертикальной Y и горизонтальной X составляющими реакции R. X и Y найдем из уравнений статики:



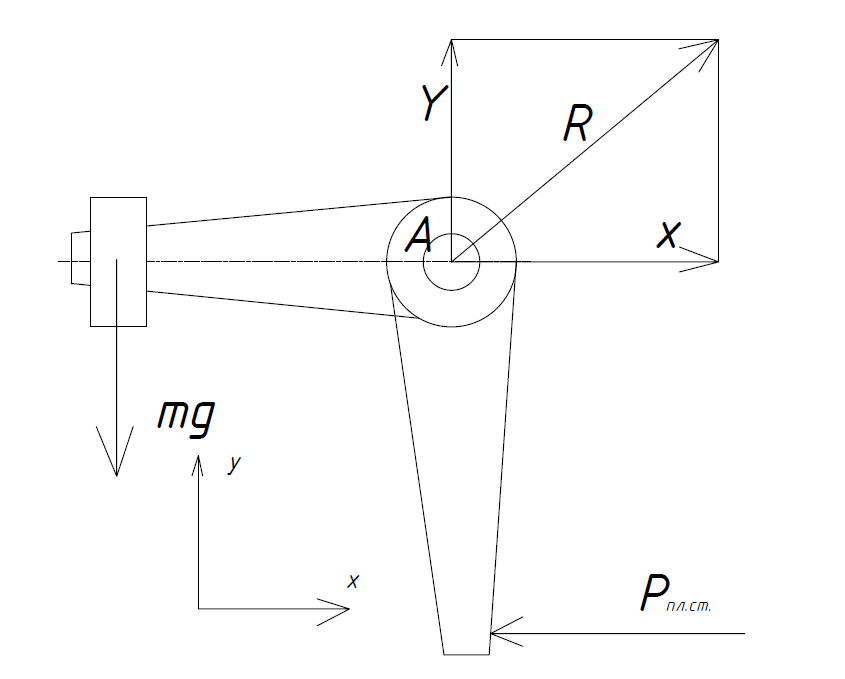
∑F_x = 0 => X- P_пл.ст = 0 => X = P_пл.ст =

= 14700 Н

∑F_y = 0 => Y- m·g = 0 => Y= m·g = 856 кг ·9,8 = 8388,8 Н

Полную реакцию R найдем с помощью теоремы Пифагора:

R= 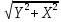= 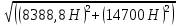≈ 16925 Н ≈ 16,9 кН

2. Для определения наименьшего вакуума p_в над уровнем воды, который необходим для удержания щита в равновесии без груза, будем исходить из того, что в этом случае P_пл.ст должна проходить через центр тяжести щита, то есть p_с = 0. Такое возможно, если П.П проходит через точку С. Зная, что расстояние между поверхностью воды и П.П определяется формулой:

L = 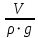, где V – показание вакууметра (искомый вакуум), можно найти p_в:

p_в = L·ρ·g = 1,5 м · 1000 · 9,8 = 14700 Па = 14,7 кПа.

Таким образом:

m = 856 кг;

R = 16,9 кН;

p_{в =} 14,7 кПа.

За это решение спасибо Домбровской Злате ♥

---

Смотрите также файлы

• Сафи тебаев атындаы аунг кеа 6В07101ндірісті автоматтандыру жне басару.docx

• Политические интересы 4 Политические отношения 9.docx

• Профилактика клещевого энцефалита и боррелиоза Медицинская сестра кабинета инфекционных заболеваний гауз то городская поликлиника 3.pptx

• Контрольная работа дисциплина Сервис индустрии гостеприимства.docx

• Ребят необходимо учить чувствовать, понимать, ценить и, что самое главное, творить красоту. Нужно делать все, чтобы само помещение школы, её территория были притягательными, в чемто волшебными.docx