Файл: Задача преподавания геометрии развить у учащихся соответствующие три качества пространственное воображение, практическое понимание и логическое мышление. При этом решаются следующие задачи.docx
Добавлен: 07.12.2023
Просмотров: 43
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
k' такой, что , и все внутренние точки лежат в заданной полуплоскости. Каждый угол равен самому себе: .
III5 Пусть А, В, С - три точки, не лежащие на одной прямой, и - тоже три точки, не лежащие на одной прямой. Если при этом и , то и .
Сравним эту группу аксиом с аксиомами учебника Атанасяна.
Во-первых: Гильберт не использует такое понятие как "наложение".
Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
Также нет в аксиомах Гильберта такого понятия как "неразвернутый угол".
От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и притом только один.
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
Во-вторых, в школьном учебнике практически нет обозначений отрезков, углов, которые используются у Гильберта, но введено такое понятие как "фигура", обозначается буквой Ф. И если у Гильберта рассматривается равенство отрезков, как в аксиоме III2, то у Атанасяна рассматривается равенство фигур.
Если фигура Ф равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.
Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
В аксиоме Гильберта III4 имеется утверждение: Каждый угол равен самому себе: . В аксиоматике Атанасяна имеется отдельная аксиома:
Любая фигура равна самой себе.
Имеется также аксиома, показывающая совмещение углов наложением:
Два равных угла hk и h1k1, лежащие в плоскостях, являющихся границами полупространств P и P1, можно совместить наложением так, что при этом совместятся полупространства P и P1, причем это можно сделать двумя способами: в одном случае совместятся лучи h и h1, k и k1, а в другом лучи h и k1, k и h1.
IV группа. Аксиомы непрерывности
Основное назначение этой группы аксиом состоит в том, чтобы ввести длину отрезка и величину угла, а также описать свойства непрерывности расположения точек на прямой.
IV1. Пусть АВ и CD - произвольные отрезки. Тогда на луче АВ существует конечное число точек
, расположенных так, что точка А1лежит между А и А2, точка А2лежит между А1, и А3и т.д., отрезки равны отрезку СD иточка В лежит между А и Ап.
IV2. Пусть, на какой угодно прямой а, дана бесконечная последовательность отрезков , из которых каждый последующий лежит внутри предыдущего; пусть далее, каким бы ни был заранее данный отрезок, найдется номер n, для которого меньше этого отрезка. Тогда на прямой а существует точка, лежащая внутри всех отрезков .
В учебнике Атанасяна эта группа аксиом представлена двумя аксиомами, которые характеризуют измерение отрезков:
При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.
V группа Аксиома параллельности
У Гильберта данная аксиома звучит так:
V. Даны: прямая а и, не принадлежащая ей, точка A. В плоскости, определяемой прямой а и точкой A, существует не более одной прямой, проходящей через точку A и параллельной прямой а.
В учебнике Атанасяна дана очень схожая формулировка, не имеющая, правда обозначений для плоскости, прямой и точки.
В любой плоскости через точку, не лежащую на данной прямой этой плоскости, проходит только одна прямая, параллельная данной.
29. Рассуждение с целью обоснования истинности какого-либо утверждения есть доказательство. Существуют различные методы доказательства теорем. Под методом доказательствабудем понимать способ связи аргументов при переходе от условия к заключению суждения. Методы доказательства, используемые в школьном курсе математики, можно выделить по двум основаниям: по пути обоснования тезиса (прямое и косвенное); по математическому аппарату, используемому в доказательстве.
К прямым приемам доказательстваотносятся:
1. Прием преобразования условия суждения (синтетический).
2. Прием преобразования заключения суждения: а) отыскание достаточных оснований справедливости заключения (восходящий анализ); б) отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ).
3. Прием последовательного преобразования то условия, то заключения суждения.
К косвенным приемам поиска доказательствотносятся:
1. Метод “от противного” (истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения).
2. Разделительный метод или метод разделения условий (тезис рассматривается как один из возможных вариантов предположений, когда все предположения отвергаются, кроме одного), иначе этот метод называют методом исключения.
К методам доказательства, выделенным по второму основанию, когда способ связи аргументов согласуется с определенной математической теорией в школьном курсе математики, относятся:
1. Метод геометрических преобразований. Этот метод в школе используется как средство обоснования некоторых отношений между элементами евклидовой геометрии. Состоит он из выполнения последовательности шагов: выбирается геометрическое преобразование, обладающее свойством, которое позволяет обосновать наличие указанного отношения между объектами евклидовой геометрии; выполняется преобразование, при котором один объект переходит в другой; обосновывается наличие указанного отношения между объектами с помощью свойств выбранного геометрического преобразования.
2. Алгебраические методы(уравнений, неравенств, тождественных преобразований).
3. Векторный метод,использующий аппарат векторной алгебры.
4. Координатный метод, Координатный метод - это способ определения положения точки на прямой, на плоскости или в пространстве с помощью чисел (например, в декартовой системы координат ли какой-либо другой). Используя координатный метод, алгебраические уравнения можно истолковать в виде геометрических образов (графиков или фигур) и, наоборот, искать решение геометрических задач с помощью аналитических выражений (уравнений, неравенств или их систем).
30.
Методические рекомендации по решению задач геометрическим методом
1. При решении задач геометрическим методом используются теоремы и факты проективной геометрии, например, теоремы Паппа, Дезарга, Паскаля, Брианшона, свойства полного четырехвершинника.
2. При решении задач геометрическим методом из данных задачи необходимо выделить какую-либо известную фигуру или комбинацию нескольких фигур проективной плоскости, например, два трехвершинника, шестивершинник, вписанный в овальную линию второго порядка, шестисторонник, описанный около овальной линии второго порядка, полный четырехвершинник и др..
3. Чтобы применить проективную теорему, необходимо: а) четко выделить в формулировке этой теоремы условие и заключение; б) пользуясь условием задачи, а также свойствами данных фигур, доказать, что выполняется условие теоремы; в) применить теорему и сделать соответствующее заключение.
В основной школе традиционно изучается курс планиметрии, содержание которого определяется “Программой для общеобразовательных школ, гимназий, лицеев: Математика. 5-11 классы” [17]. Оно группируется вокруг нескольких стержневых содержательно-методических линий: “Геометрические фигуры и их свойства”, “Геометрические величины”, “Векторы”.
Наибольшую остроту в обсуждении вопросов содержания курса планиметрии приобрел вопрос о включении в него линии геометрических преобразований.
В настоящее время этот вопрос решен в пользу традиционного содержания: геометрические преобразования изучаются как периферийный вопрос курса.
Вернемся к основным содержательно-методическим линиям курса планиметрии. Вопросы их изучения будут подробно рассматриваться далее. Сейчас же ограничимся краткими пояснениями.
Раздел “Геометрические фигуры и их свойства” является основным. Его изучению посвящен материал 7-го класса, значительная часть материала 8-го и 9-го классов. Изложение практически во всех учебниках ведется традиционно. Аналогично обстоит дело с содержательно-методической линией “Геометрические величины”: она представлена также преимущественно традиционно, появляясь в курсе планиметрии по мере надобности.
Векторы впервые вошли в курс геометрии отечественной школы только в середине 70-х годов XX в. и получили всеобщее признание в силу большой общеобразовательной значимости и обширных практических приложений. Однако методика применения векторов к решению задач, а тем более использования векторного метода в теории находится еще в стадии разработки. Поэтому векторы недостаточно широко используются в современном курсе планиметрии. С ними, по-видимому, могут быть связаны перспективы курса, как, впрочем, и с линией геометрических преобразований.
Основное содержание школьного курса планиметрии своими истоками имеет “Начала” Евклида. Все попытки “отойти от Евклида”, в том числе предпринимавшиеся в отечественном образовании в 70-е годы XX в., оказались неудачными.
31. Задачи выделения из всей совокупности решений такого решения, которое обладает некоторым свойством в максимальной или минимальной степени, обычно называются экстремальными или оптимизационными. Приведем примеры экстремальных комбинаторных задач.
1) Задача коммивояжера: заключается в отыскании самого выгодного маршрута, проходящего через указанные города точно по одному разу с последующим возвратом в исходный город.
2) Задача о рюкзаке. Постановка задачи следующая. Пусть имеется набор предметов, каждый из которых имеет два параметра — вес и ценность, и есть рюкзак, определенной вместимости. Задача заключается в том, чтобы собрать рюкзак с максимальной ценностью предметов внутри, соблюдая при этом весовое ограничение рюкзака.
3) Задача о назначениях - задача о наилучшем распределении некоторого числа работ между таким же числом исполнителей при условии взаимно однозначного соответствия между множествами работ и исполнителей.
4) Задачи теории расписаний. В этих задачах требования обслуживаются приборами и нужно составить такие перестановки обслуживания требований, которые были бы оптимальными по тому или иному критерию.
32. https://univerlib.com/mathematical_analysis/limit_sequence/infinite_sequence/
33. https://www.hse.ru/data/2010/10/25/1222763003/Лекция%2004.pdf страница 10
34. http://math4school.ru/predel_neprerivnost_funkcii.html
35. https://infotables.ru/matematika/59-differentsialnoe-ischislenie/583-ponyatie-proizvodnoj
36.
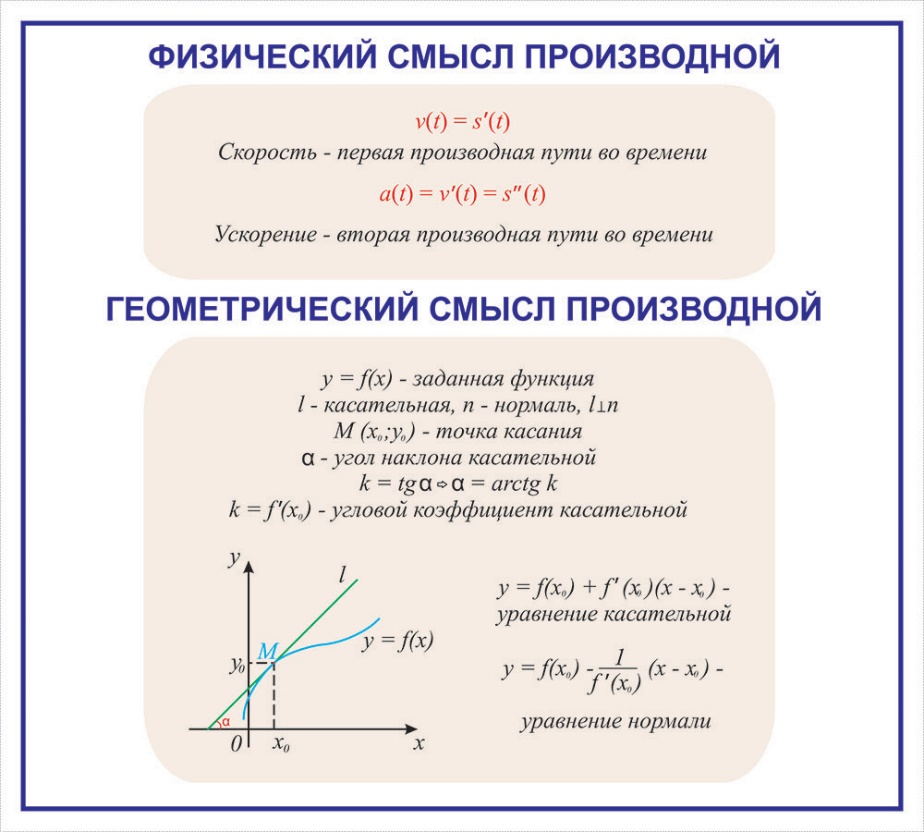
37. Что такое исследование функции
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная
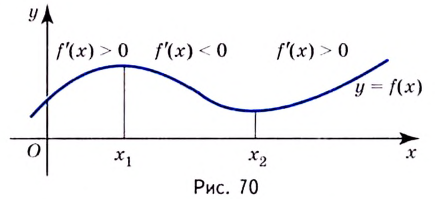
Правильными будут следующие утверждения.
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция
III5 Пусть А, В, С - три точки, не лежащие на одной прямой, и - тоже три точки, не лежащие на одной прямой. Если при этом и , то и .
Сравним эту группу аксиом с аксиомами учебника Атанасяна.
Во-первых: Гильберт не использует такое понятие как "наложение".
Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.
Также нет в аксиомах Гильберта такого понятия как "неразвернутый угол".
От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и притом только один.
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
Во-вторых, в школьном учебнике практически нет обозначений отрезков, углов, которые используются у Гильберта, но введено такое понятие как "фигура", обозначается буквой Ф. И если у Гильберта рассматривается равенство отрезков, как в аксиоме III2, то у Атанасяна рассматривается равенство фигур.
Если фигура Ф равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.
Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
В аксиоме Гильберта III4 имеется утверждение: Каждый угол равен самому себе: . В аксиоматике Атанасяна имеется отдельная аксиома:
Любая фигура равна самой себе.
Имеется также аксиома, показывающая совмещение углов наложением:
Два равных угла hk и h1k1, лежащие в плоскостях, являющихся границами полупространств P и P1, можно совместить наложением так, что при этом совместятся полупространства P и P1, причем это можно сделать двумя способами: в одном случае совместятся лучи h и h1, k и k1, а в другом лучи h и k1, k и h1.
IV группа. Аксиомы непрерывности
Основное назначение этой группы аксиом состоит в том, чтобы ввести длину отрезка и величину угла, а также описать свойства непрерывности расположения точек на прямой.
IV1. Пусть АВ и CD - произвольные отрезки. Тогда на луче АВ существует конечное число точек
, расположенных так, что точка А1лежит между А и А2, точка А2лежит между А1, и А3и т.д., отрезки равны отрезку СD иточка В лежит между А и Ап.
IV2. Пусть, на какой угодно прямой а, дана бесконечная последовательность отрезков , из которых каждый последующий лежит внутри предыдущего; пусть далее, каким бы ни был заранее данный отрезок, найдется номер n, для которого меньше этого отрезка. Тогда на прямой а существует точка, лежащая внутри всех отрезков .
В учебнике Атанасяна эта группа аксиом представлена двумя аксиомами, которые характеризуют измерение отрезков:
При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.
V группа Аксиома параллельности
У Гильберта данная аксиома звучит так:
V. Даны: прямая а и, не принадлежащая ей, точка A. В плоскости, определяемой прямой а и точкой A, существует не более одной прямой, проходящей через точку A и параллельной прямой а.
В учебнике Атанасяна дана очень схожая формулировка, не имеющая, правда обозначений для плоскости, прямой и точки.
В любой плоскости через точку, не лежащую на данной прямой этой плоскости, проходит только одна прямая, параллельная данной.
29. Рассуждение с целью обоснования истинности какого-либо утверждения есть доказательство. Существуют различные методы доказательства теорем. Под методом доказательствабудем понимать способ связи аргументов при переходе от условия к заключению суждения. Методы доказательства, используемые в школьном курсе математики, можно выделить по двум основаниям: по пути обоснования тезиса (прямое и косвенное); по математическому аппарату, используемому в доказательстве.
К прямым приемам доказательстваотносятся:
1. Прием преобразования условия суждения (синтетический).
2. Прием преобразования заключения суждения: а) отыскание достаточных оснований справедливости заключения (восходящий анализ); б) отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений (нисходящий анализ).
3. Прием последовательного преобразования то условия, то заключения суждения.
К косвенным приемам поиска доказательствотносятся:
1. Метод “от противного” (истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения).
2. Разделительный метод или метод разделения условий (тезис рассматривается как один из возможных вариантов предположений, когда все предположения отвергаются, кроме одного), иначе этот метод называют методом исключения.
К методам доказательства, выделенным по второму основанию, когда способ связи аргументов согласуется с определенной математической теорией в школьном курсе математики, относятся:
1. Метод геометрических преобразований. Этот метод в школе используется как средство обоснования некоторых отношений между элементами евклидовой геометрии. Состоит он из выполнения последовательности шагов: выбирается геометрическое преобразование, обладающее свойством, которое позволяет обосновать наличие указанного отношения между объектами евклидовой геометрии; выполняется преобразование, при котором один объект переходит в другой; обосновывается наличие указанного отношения между объектами с помощью свойств выбранного геометрического преобразования.
2. Алгебраические методы(уравнений, неравенств, тождественных преобразований).
3. Векторный метод,использующий аппарат векторной алгебры.
4. Координатный метод, Координатный метод - это способ определения положения точки на прямой, на плоскости или в пространстве с помощью чисел (например, в декартовой системы координат ли какой-либо другой). Используя координатный метод, алгебраические уравнения можно истолковать в виде геометрических образов (графиков или фигур) и, наоборот, искать решение геометрических задач с помощью аналитических выражений (уравнений, неравенств или их систем).
30.
Методические рекомендации по решению задач геометрическим методом
1. При решении задач геометрическим методом используются теоремы и факты проективной геометрии, например, теоремы Паппа, Дезарга, Паскаля, Брианшона, свойства полного четырехвершинника.
2. При решении задач геометрическим методом из данных задачи необходимо выделить какую-либо известную фигуру или комбинацию нескольких фигур проективной плоскости, например, два трехвершинника, шестивершинник, вписанный в овальную линию второго порядка, шестисторонник, описанный около овальной линии второго порядка, полный четырехвершинник и др..
3. Чтобы применить проективную теорему, необходимо: а) четко выделить в формулировке этой теоремы условие и заключение; б) пользуясь условием задачи, а также свойствами данных фигур, доказать, что выполняется условие теоремы; в) применить теорему и сделать соответствующее заключение.
В основной школе традиционно изучается курс планиметрии, содержание которого определяется “Программой для общеобразовательных школ, гимназий, лицеев: Математика. 5-11 классы” [17]. Оно группируется вокруг нескольких стержневых содержательно-методических линий: “Геометрические фигуры и их свойства”, “Геометрические величины”, “Векторы”.
Наибольшую остроту в обсуждении вопросов содержания курса планиметрии приобрел вопрос о включении в него линии геометрических преобразований.
В настоящее время этот вопрос решен в пользу традиционного содержания: геометрические преобразования изучаются как периферийный вопрос курса.
Вернемся к основным содержательно-методическим линиям курса планиметрии. Вопросы их изучения будут подробно рассматриваться далее. Сейчас же ограничимся краткими пояснениями.
Раздел “Геометрические фигуры и их свойства” является основным. Его изучению посвящен материал 7-го класса, значительная часть материала 8-го и 9-го классов. Изложение практически во всех учебниках ведется традиционно. Аналогично обстоит дело с содержательно-методической линией “Геометрические величины”: она представлена также преимущественно традиционно, появляясь в курсе планиметрии по мере надобности.
Векторы впервые вошли в курс геометрии отечественной школы только в середине 70-х годов XX в. и получили всеобщее признание в силу большой общеобразовательной значимости и обширных практических приложений. Однако методика применения векторов к решению задач, а тем более использования векторного метода в теории находится еще в стадии разработки. Поэтому векторы недостаточно широко используются в современном курсе планиметрии. С ними, по-видимому, могут быть связаны перспективы курса, как, впрочем, и с линией геометрических преобразований.
Основное содержание школьного курса планиметрии своими истоками имеет “Начала” Евклида. Все попытки “отойти от Евклида”, в том числе предпринимавшиеся в отечественном образовании в 70-е годы XX в., оказались неудачными.
31. Задачи выделения из всей совокупности решений такого решения, которое обладает некоторым свойством в максимальной или минимальной степени, обычно называются экстремальными или оптимизационными. Приведем примеры экстремальных комбинаторных задач.
1) Задача коммивояжера: заключается в отыскании самого выгодного маршрута, проходящего через указанные города точно по одному разу с последующим возвратом в исходный город.
2) Задача о рюкзаке. Постановка задачи следующая. Пусть имеется набор предметов, каждый из которых имеет два параметра — вес и ценность, и есть рюкзак, определенной вместимости. Задача заключается в том, чтобы собрать рюкзак с максимальной ценностью предметов внутри, соблюдая при этом весовое ограничение рюкзака.
3) Задача о назначениях - задача о наилучшем распределении некоторого числа работ между таким же числом исполнителей при условии взаимно однозначного соответствия между множествами работ и исполнителей.
4) Задачи теории расписаний. В этих задачах требования обслуживаются приборами и нужно составить такие перестановки обслуживания требований, которые были бы оптимальными по тому или иному критерию.
32. https://univerlib.com/mathematical_analysis/limit_sequence/infinite_sequence/
33. https://www.hse.ru/data/2010/10/25/1222763003/Лекция%2004.pdf страница 10
34. http://math4school.ru/predel_neprerivnost_funkcii.html
35. https://infotables.ru/matematika/59-differentsialnoe-ischislenie/583-ponyatie-proizvodnoj
36.

37. Что такое исследование функции
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная

Правильными будут следующие утверждения.
-
Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает. -
Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает. -
Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция