ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 55
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
по лабораторной работе №9
по дисциплине «Теоретические основы электротехники»
Тема: ИССЛЕДОВАНИЕ ИНДУКТИВНО СВЯЗАННЫХ ЦЕПЕЙ
| Студент гр. 1207 | | Коренев К.А. |
| Преподаватель | | Козулина Т.П. |
Санкт-Петербург
2023
Цель работы: экспериментальное определение параметров двух индуктивно
связанных катушек и проверка основных соотношений индуктивно связанных
цепей при различных соединениях катушек.
Общие теоретические положения
С
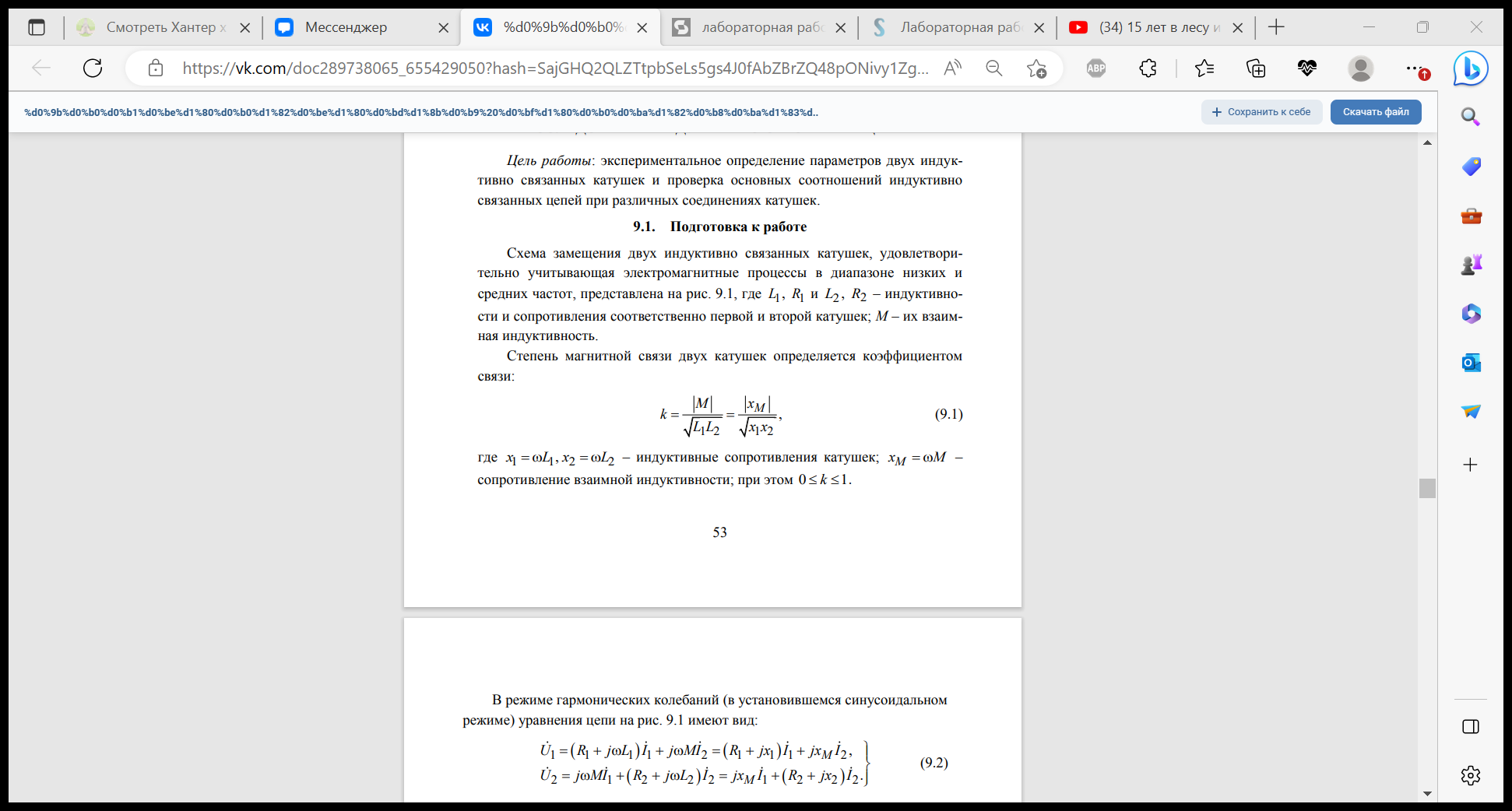
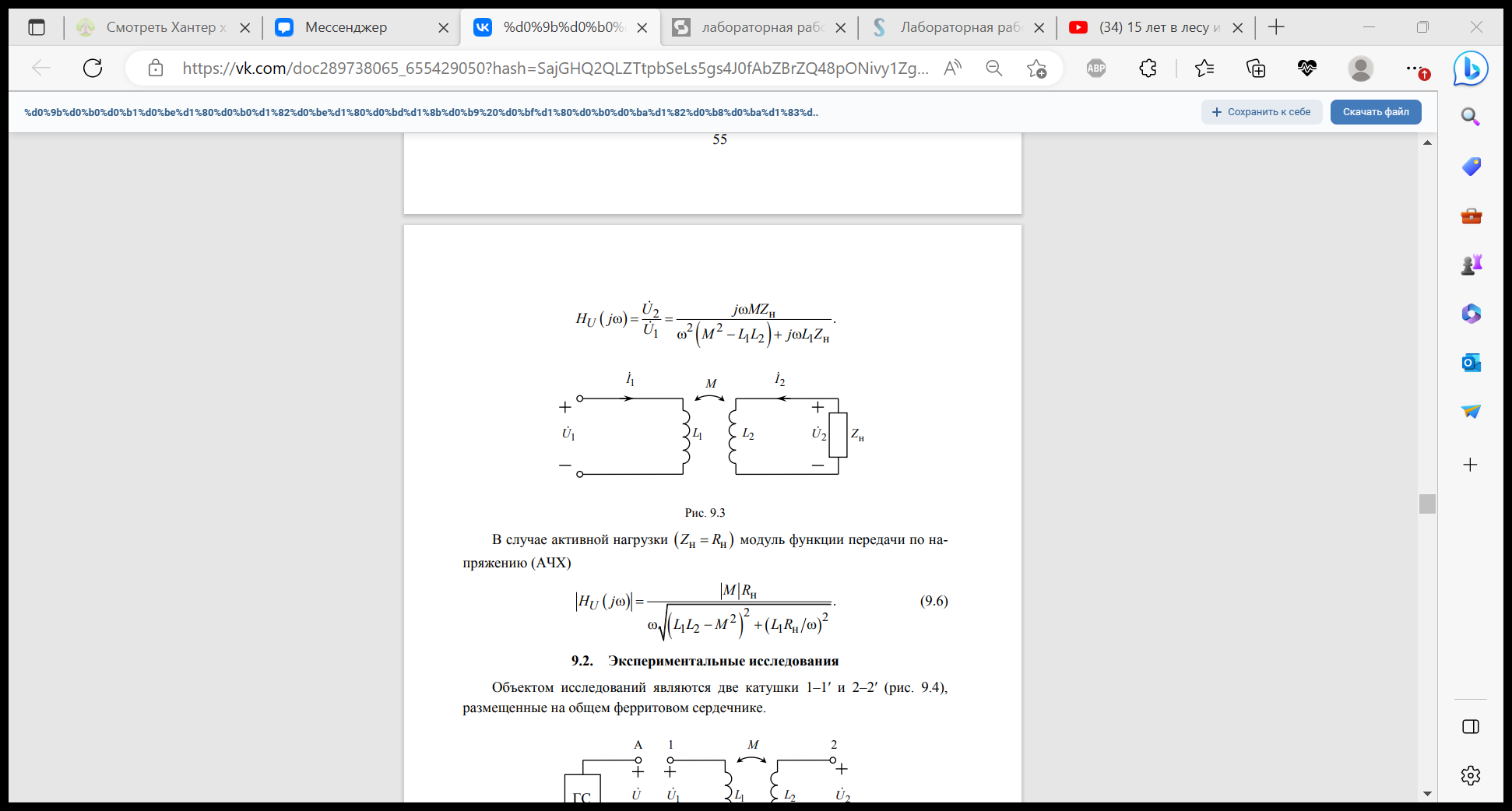
хема замещения двух индуктивно связанных катушек, удовлетворительно учитывающая электромагнитные процессы в диапазоне низких и средних частот, представлена на рис. 9.1, где L1, R1 и L2 , R2 – индуктивности и сопротивления соответственно первой и второй катушек; M – их взаимная индуктивность. Степень магнитной связи двух катушек определяется коэффициентом связи: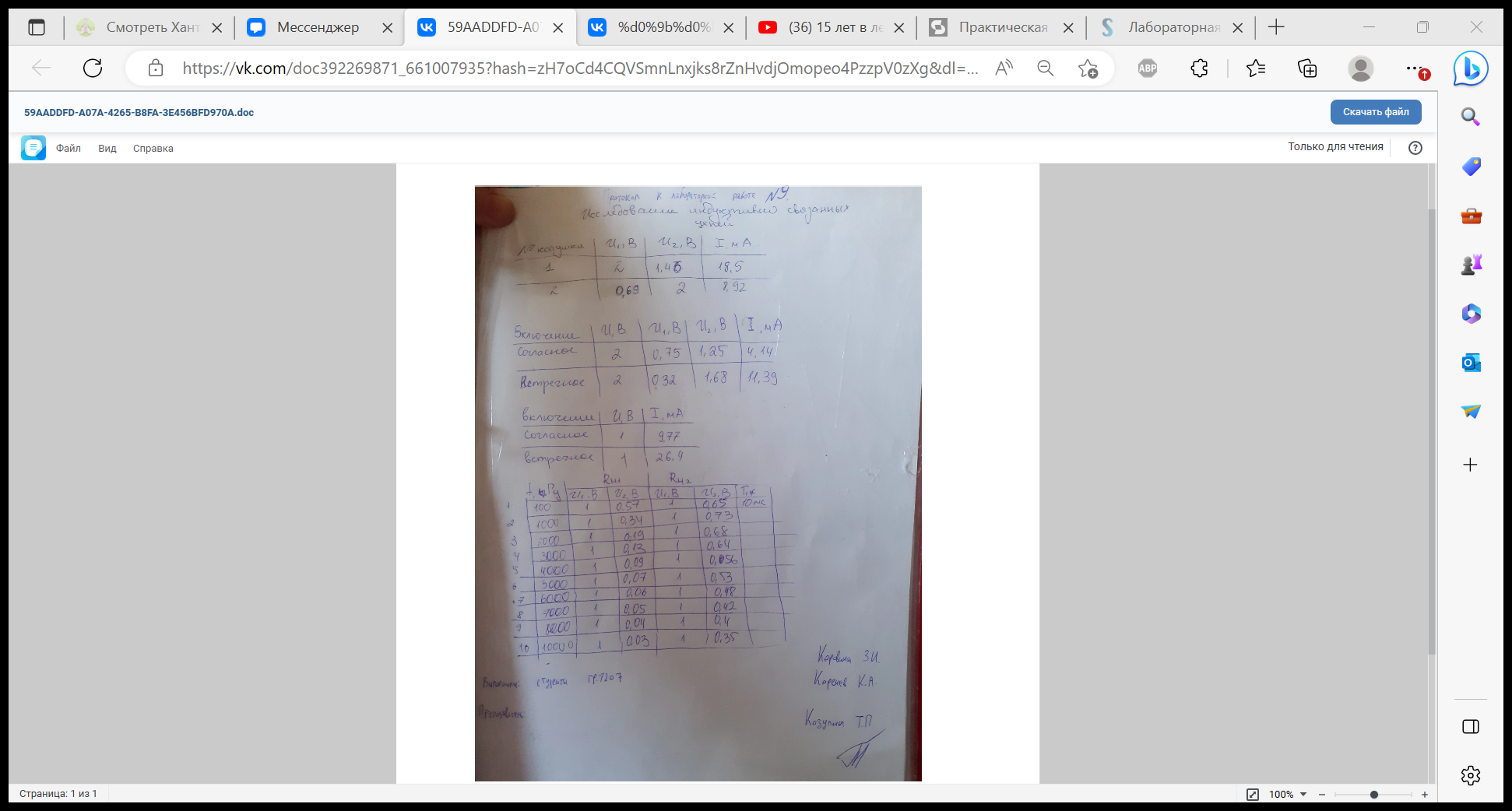
Обработка результатов
-
Определение индуктивностей катушек, взаимной индуктивности и коэффициента связи.
Пример расчета для катушки номер 1:
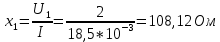
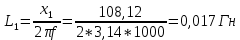
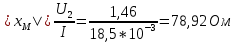
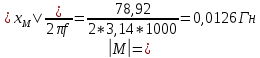
Аналогично для второй катушки. Результаты занесены в таблицу 1.
| Номер Катушки | Наблюдения | Вычисления | |||||
| U1, В | U2, В | I, мА | x, Ом | L, Гн | |xM|, Ом | |M|, Гн | |
| 1 | 2 | 1,46 | 18,5 | 108,11 | 0,017 | 78,92 | 0,0126 |
| 2 | 0,69 | 2 | 8,92 | 224,22 | 0,036 | 77,35 | 0,0123 |
Таблица 1
Расчет коэффициента связи двух катушек:
-
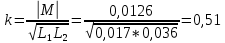
Исследование последовательного соединения индуктивно связанных катушек.
Пример расчета для согласного включения катушек:
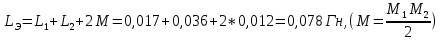
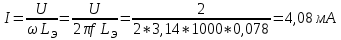
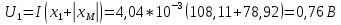
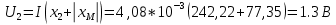
Для встречного включения расчеты аналогичные, однако взаимная индуктивность M в данном случае отрицательная.
Результаты занесены в таблицу 2.
| Включение | Наблюдения | Вычисления | |||||||
| U, В | U1, В | U2, В | I, мА | I, мА | U1, В | U2, В | LЭ, Гн | ||
| Согласное | 2 | 0,75 | 1,25 | 4,14 | 4,08 | 0,76 | 1,24 | 0,078 | |
| Встречное | 2 | 0,32 | 1,68 | 11,39 | 11,46 | 0,33 | 1,67 | 0,028 | |
Таблица 2
-
Исследование параллельного соединения индуктивно связанных катушек.
Пример расчета для согласного включения катушек:
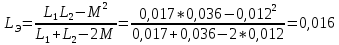
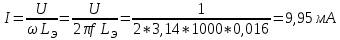
Для встречного включения расчеты аналогичные, однако взаимная индуктивность M в данном случае отрицательная.
Результаты занесены в таблицу 3.
| Включение | Наблюдения | Вычисления | ||
| U, В | I, мА | I, мА | LЭ, Гн | |
| Согласное | 1 | 9,77 | 9,95 | 0,016 |
| Встречное | 1 | 26,4 | 54,43 | 0,006 |
Таблица 3
-
Исследование АЧХ функции передачи трансформатора по напряжению
Пример расчета для нагрузки 100 Ом на частоте 100 Гц:
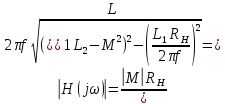
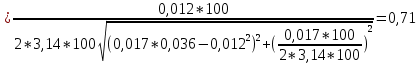
Результаты занесены в таблицу 4
| f, Гц | R1н=100 Ом | R2н=1000 Ом | |||||||||
| U1, В | U2, В | |H(jω)|=U2/U1 | U1, В | U2, В | |H(jω)|=U2/U1 | ||||||
| Опыт | Расчет | Опыт | Расчет | ||||||||
| 100 | 1 | 0,57 | 0,71 | 0,57 | 1 | 0,75 | 0,72 | 0,75 | |||
| 1000 | 1 | 0,34 | 0,37 | 0,34 | 1 | 0,73 | 0,71 | 0,73 | |||
| 2000 | 1 | 0,19 | 0,21 | 0,19 | 1 | 0,68 | 0,69 | 0,68 | |||
| 3000 | 1 | 0,13 | 0,14 | 0,13 | 1 | 0,64 | 0,65 | 0,64 | |||
| 4000 | 1 | 0,09 | 0,107 | 0,09 | 1 | 0,56 | 0,60 | 0,56 | |||
| 5000 | 1 | 0,07 | 0,086 | 0,07 | 1 | 0,53 | 0,554 | 0,53 | |||
| 6000 | 1 | 0,06 | 0,071 | 0,06 | 1 | 0,48 | 0,51 | 0,48 | |||
| 7000 | 1 | 0,05 | 0,061 | 0,05 | 1 | 0,42 | 0,47 | 0,42 | |||
| 8000 | 1 | 0,04 | 0,054 | 0,04 | 1 | 0,4 | 0,43 | 0,4 | |||
| 10000 | 1 | 0,03 | 0,043 | 0,03 | 1 | 0,35 | 0,37 | 0,35 | |||
Таблица 4
Р
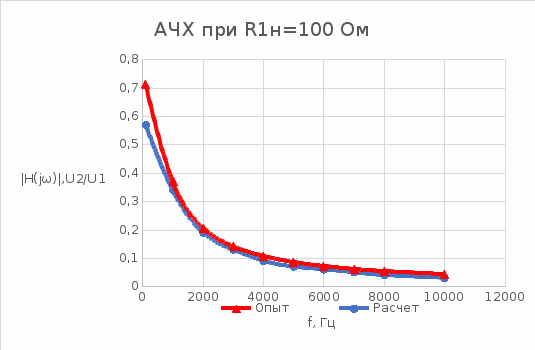исунок 1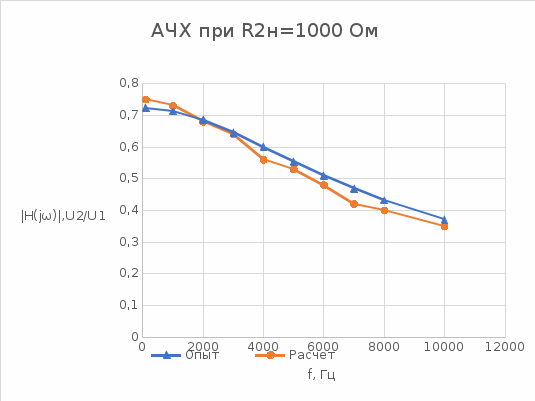
Рисунок 2
Контрольные вопросы:
1)Как установить правильность выполнения проведенных исследований?
Правильность исследования проверяется путем вычисления xM; при исследовании последовательного соединения – с помощью уравнений Кирхгофа.
2)Как практически разметить однополярные выводы двух индуктивно-связанных катушек?
Разметить катушки так, чтобы для согласного включения ток был направлен симметрично с однополярными выводами, для встречного – не симметрично.
3)При каком соотношении между параметрами катушек L1, L2 и M напряжение одной из них в режиме гармонических колебаний при последовательном соединении катушек и встречном включении будет отставать от тока?
При L1 меньше M или L2 меньше М.
4)Почему АЧХ трансформатора падает в области низких и высоких частот? В какой частотной области исследуемый трансформатор приближается к идеальному? Почему на нулевой частоте сигнал через трансформатор к нагрузке не проходит?
Исследуемый трансформатор близок к идеальному на средних частотах, где АЧХ приближается к прямой. Шунтирующее действие ограничивает передачу сигнала на низких частотах
5)Чем объяснить резкое расхождение расчетных и опытных значений |H(jω)|, при ω стремящейся к 0?
Расчет ведется для идеального трансформатора, а в реальном трансформаторе функция передачи с ограниченной полосой частот, у которой ширина определяется значениями параметров трансформатора.
Вывод:
В ходе выполнения лабораторной работы определили индуктивности катушек, взаимную индуктивность (таблица 1). Для катушек был найден коэффициент связи, который равен 0,51, что соответствует теории, т.к. в пространстве катушки были расположены последовательно.
Были найдены эквивалентные индуктивности при согласном и встречном подключении для последовательного и параллельного подключения (таблица 2, таблица 3). Высокая индуктивность наблюдалась при согласном включении, т.к. их потоки суммируются и взаимная индуктивность положительная. При встречном подключении напротив эквивалентная индуктивность мала.
Также в диапазоне частот 100-12000 Гц была построена амплитудно-частотная характеристика трансформатора с двумя разными нагрузками (рис.1, ри.2). Рассчитанные результаты оказались довольно точными.