Воронежский государственный лесотехнический университет

Факультет компьютерных наук и технологий

Лабораторная работа №2

«Перевод чисел из одной системы счисления в другую»

Работу выполнил:

Студентка группы Проверил: профессор

Цель работы: получение навыков выполнения перевода чисел из одной системы счисления в другую

Теоретическое введение:

Одним из распространённых методов перевода чисел является универсальный алгоритм. Кроме него, применяют перевод при помощи весов разрядов, схему Горнера и другие алгоритмы.

При использовании универсального алгоритма отдельно переводятся целая и дробная части. Для перевода целой части необходимо последовательно делить целую часть числа и образующиеся при делении целые частные, записанные в исходной системе счисления, на основание новой системы счисления, записанное в исходной системе счисления. Образующиеся на каждом шагу деления остатки представляют собой цифры разрядов числа в новой системе счисления, записанные цифрами исходной системы счисления. При этом первый остаток – это цифра младшего разряда числа, а последний остаток – цифра старшего разряда числа

Для перевода дробной части числа необходимо последовательно умножать дробную часть числа и дробные части образующихся произведений, записанные в исходной системе счисления, на основание новой системы счисления, записанное в исходной системе счисления. При этом целые части образующихся на каждом шагу умножения произведений представляют собой цифры разрядов дробной части числа в новой системе счисления, записанные в исходной системе счисления. При этом целая часть нового произведения – это старший разряд дробной части числа, стоящего справа от запятой.

Рассмотрим пример.

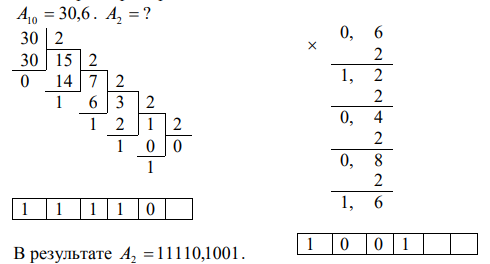
Перевод чисел с использованием весов разрядов удобно использовать для перевода из двоичной системы счисления в десятичную. Вес разряда – это число, показывающее, во сколько раз единица данного разряда больше или меньше единицы младшего разряда целой части числа. Если в формуле канонической записи числа все цифры записать в новой системе счисления и выполнить указанные в формуле арифметические действия, то получим число в новой системе счисления.

---

Пример:

1 0 0 0 1 0 1 – число

64 32 16 8 4 2 1 - веса разрядов

Просуммировав ненулевые разряды, получим: 64+4+1 = 69

Перевод чисел по схеме Горнера представляет собой вычисления по преобразованной формуле канонической формы числа, например:

Для перевода числа из одной системы счисления в другую надо:

Умножить цифру старшего разряда числа, записанную в новой системе счисления, на основание исходной системы счисления, записанное в новой системе счисления. Затем к полученному результату прибавить цифру следующего разряда числа, записанного в новой системе счисления, и полученную сумму снова умножить на основание исходной системы счисления, и так далее до последнего, младшего разряда. После прибавления младшего разряда умножение на основание системы счисления не производится.

П 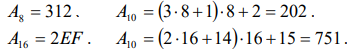римеры:

Ход работы:

Вариант 20

№1. 1)A₁₀=23 2) A₁₀=117

A₇=? A₁₁=?

-	23	7
	21	3
	2

-	117	11
	110	10
	7

А₇=32 А₁₁=А7

№2. 1) 1 1 1 1 0 1 0 1

128 64 32 16 8 4 2 1

А₂= 11110101 А₁₀ =128+64+32+16+4+1=245

2) 1 1 0 1 0

16 8 4 2 1

А₂= 11010 А₁₀ =16+8+2=26

3) 1 0 0 0 0 0 1

64 32 16 8 4 2 1

А₂= 1000001 А₁₀ =64+1=65

№3. 1) А₈= 565 А₁₀ =?

А₁₀ =

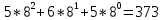
2) А₈= 124 А₁₀ =?

А₁₀ =

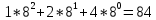
3) А₁₆= 153A А₁₀ =?

А₁₀ =

---

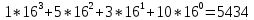
4) А₁₆= 1239 А₁₀ =?

А₁₀ =

---

Смотрите также файлы

• Методическое пособие для студентов очнозаочной формы обучения по направлению 38. 03. 02 Менеджмент профиль Менеджмент организации.docx

• План мероприятий по повышению качества образования выпускников Сроки проведения.docx

• Скорость передачи данный или пропускная способность.docx

• Негосударственные формы социального обеспечения в России Содержание.docx

• Об акулах в стихах.docx