Файл: Семинар 2 Найти неопределенные интегралы. Результат интегрирования проверить дифференцированием А, Б, В, г.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.12.2023

Просмотров: 14

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задание по дисциплине «Высшая математика»

1 курс

Семинар №2

1. Найти неопределенные интегралы. Результат интегрирования проверить дифференцированием

А) ,

Б) ,

В) ,

Г) ,

Д) .

Решение.

А) .

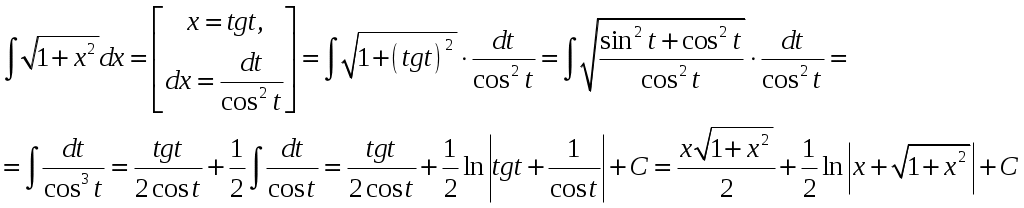
Применим подстановку , преобразуем подынтегральную функцию и находим.



Проверка:



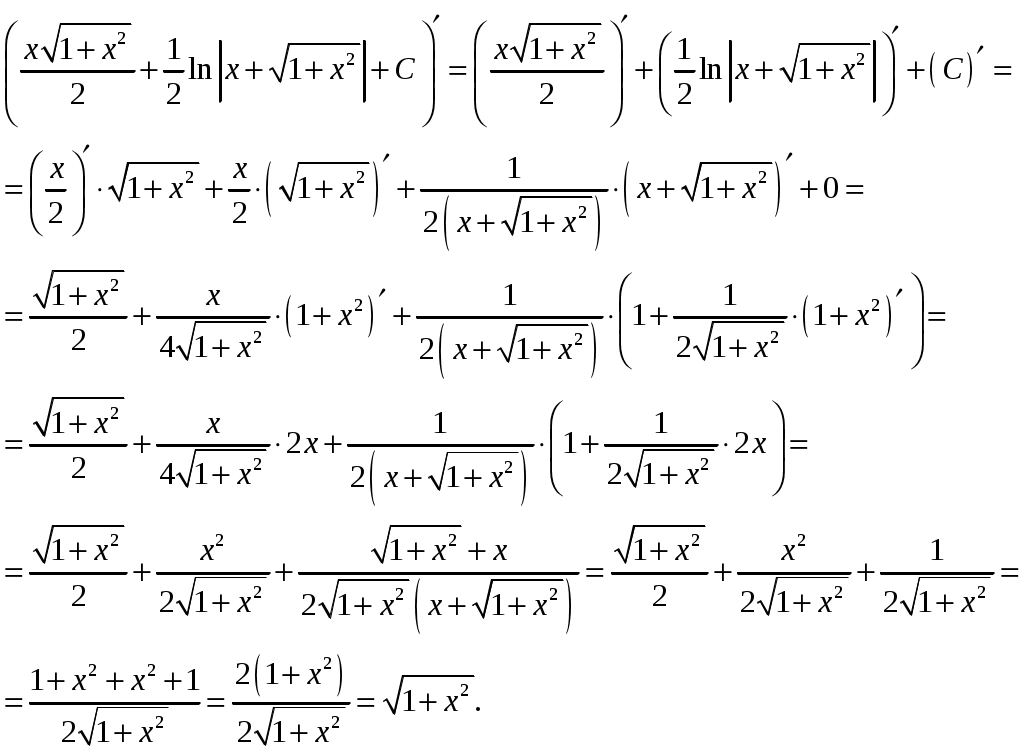
Б) .

Применим формулу интегрирования по частям .



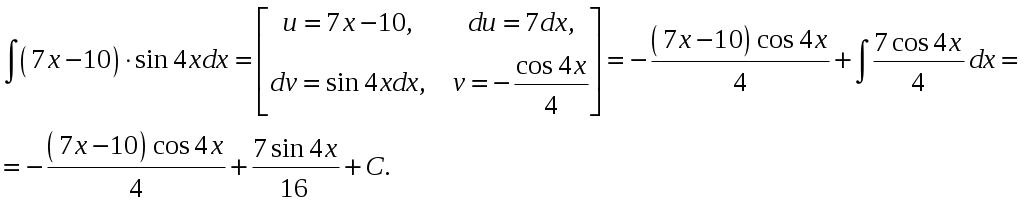
Проверка:

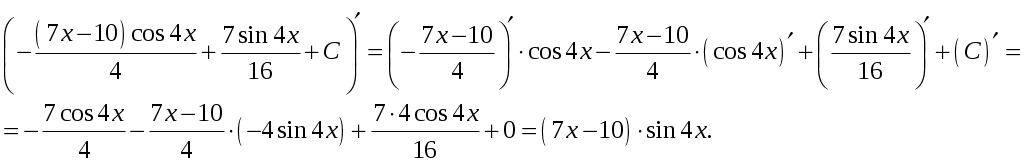В) .

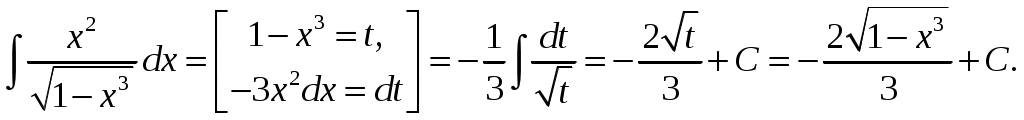
Применим подстановку , преобразуем подынтегральную функцию и находим.



Проверка:



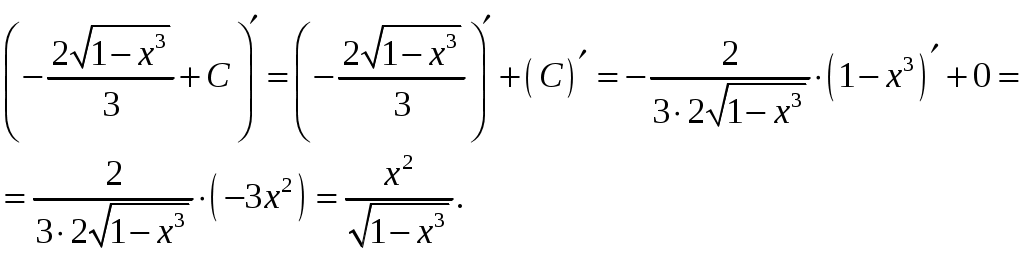
Г) .

Разложим подынтегральную дробь на простейшие:

.

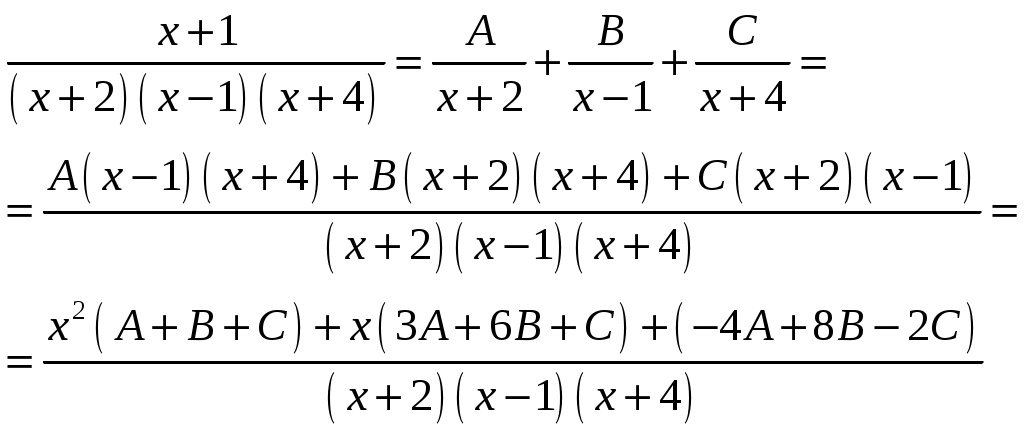
Приравнивая коэффициенты при одинаковых степенях:



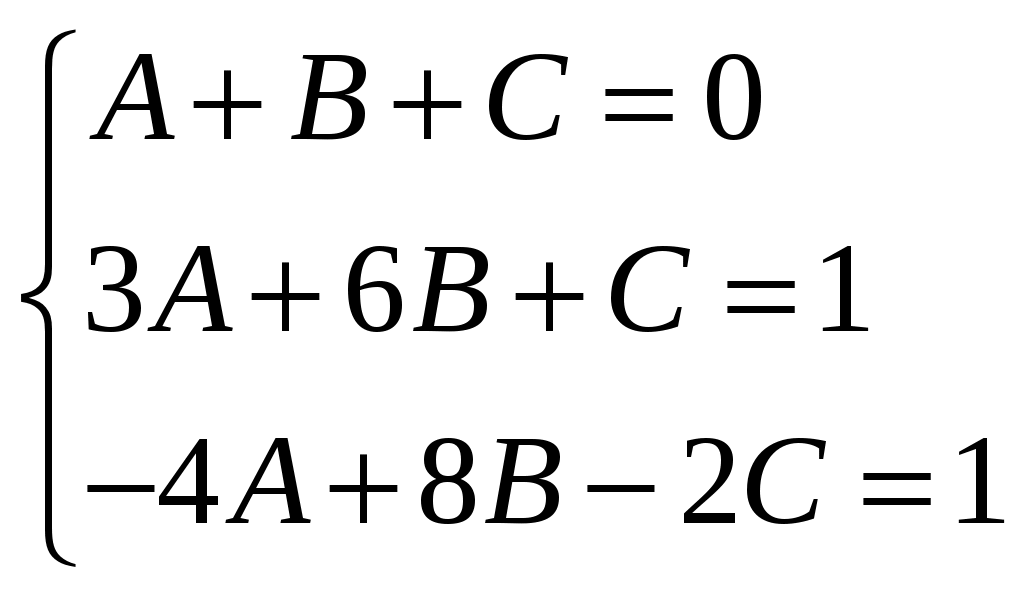
Тогда
.



Итак:



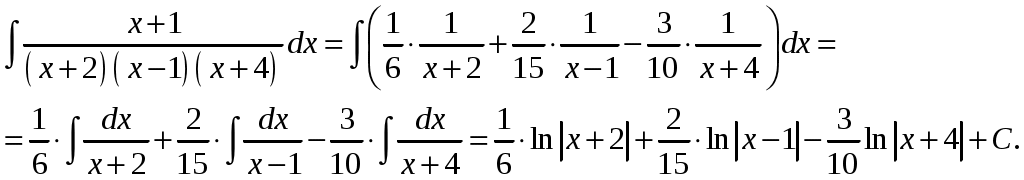
Проверка:

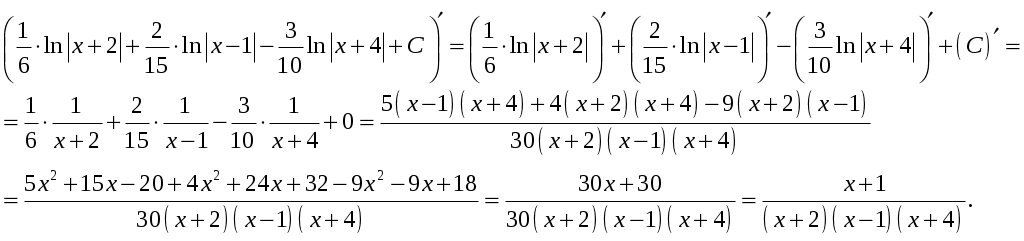Д) .

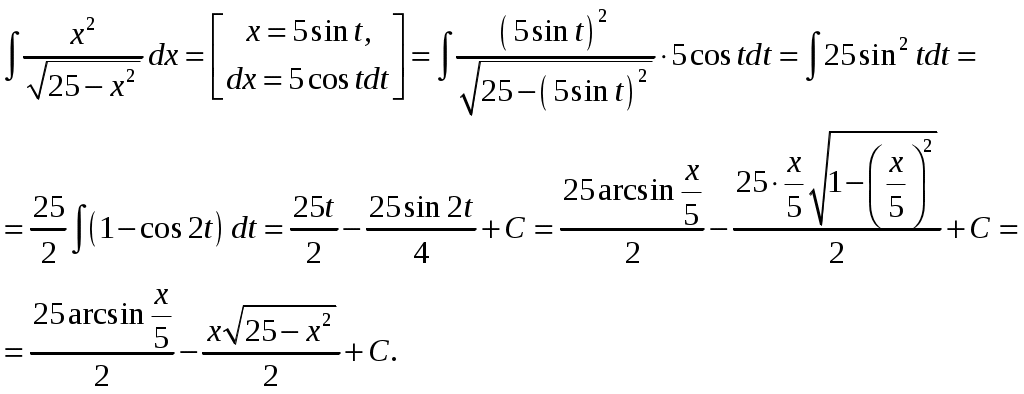
Применим подстановку , преобразуем подынтегральную функцию и находим.



Проверка:



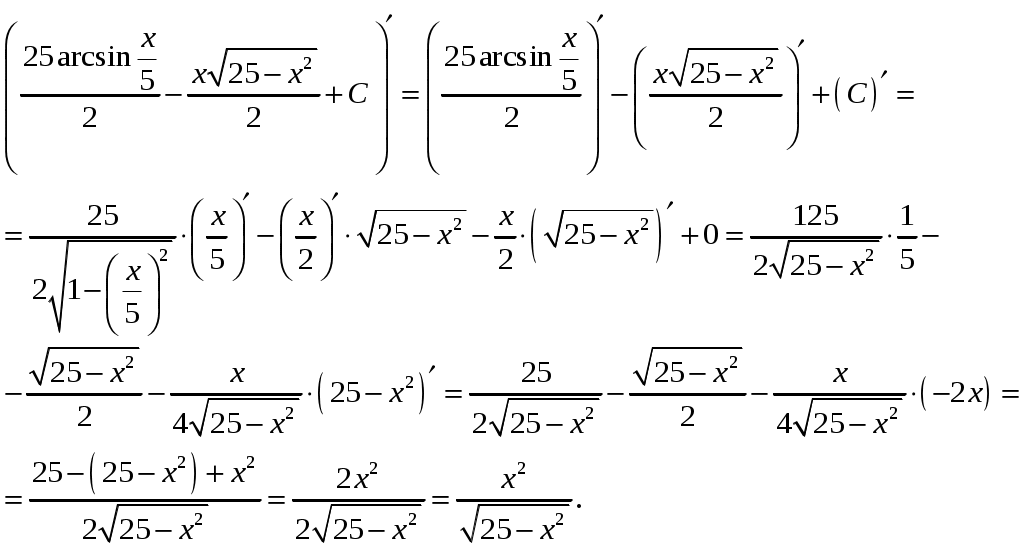
2. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.



Решение.

Строим заданные линии:



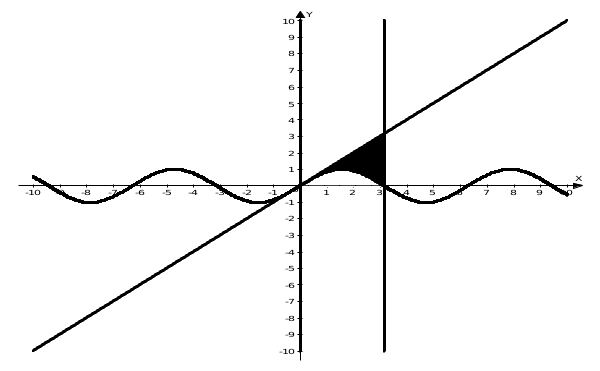
Составляем определенный интеграл:



где – линия, ограничивающая область сверху; – линия, ограничивающая область снизу; – наименьшее значение переменной x в области; – наибольшее значение переменной x в области.

В нашем случае:



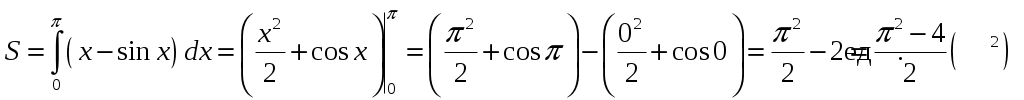
Ответ: .

3. Вычислить определенный интеграл

.

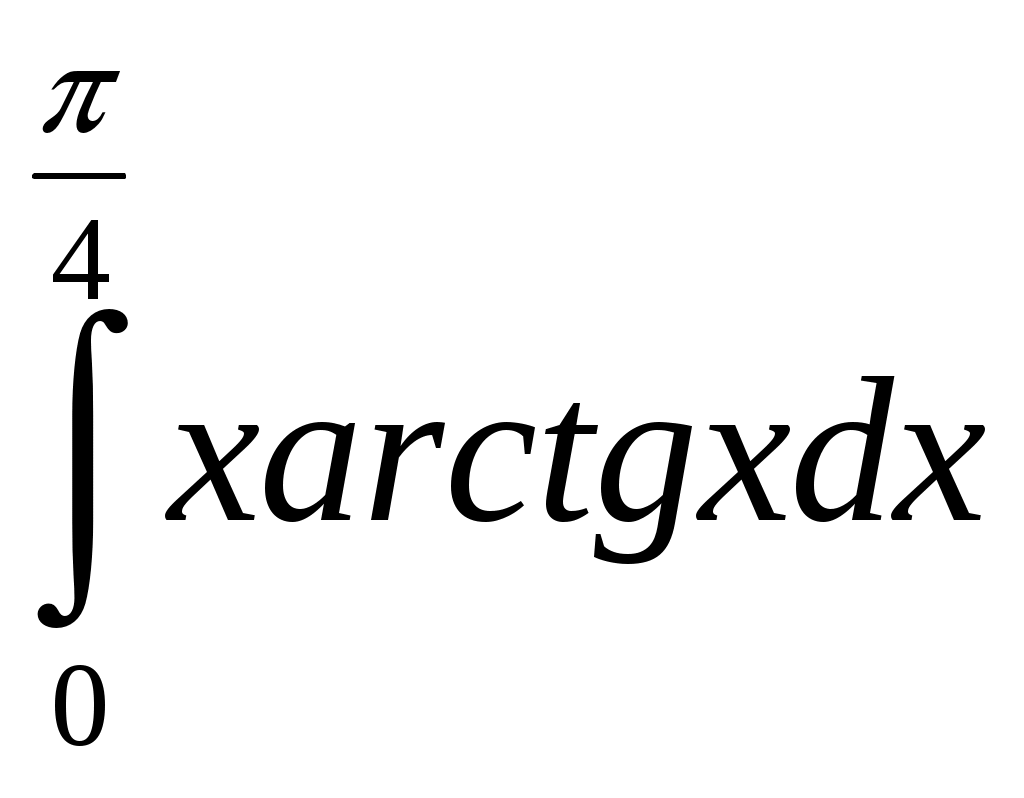Решение.

Применим формулу интегрирования по частям и формулу Ньютона-Лейбница.



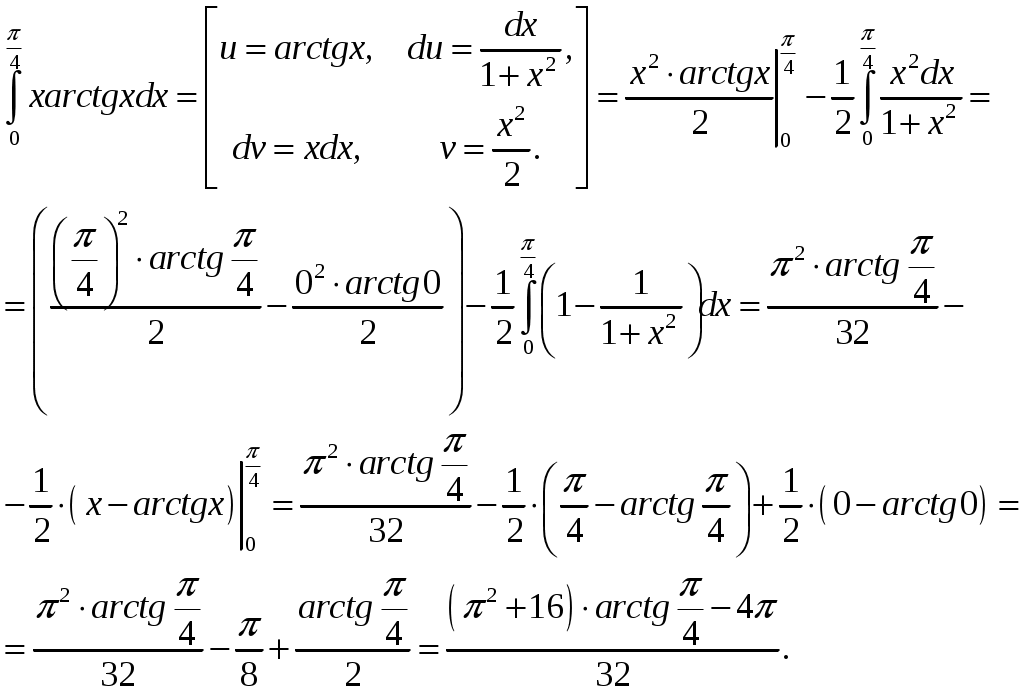
Ответ:
.

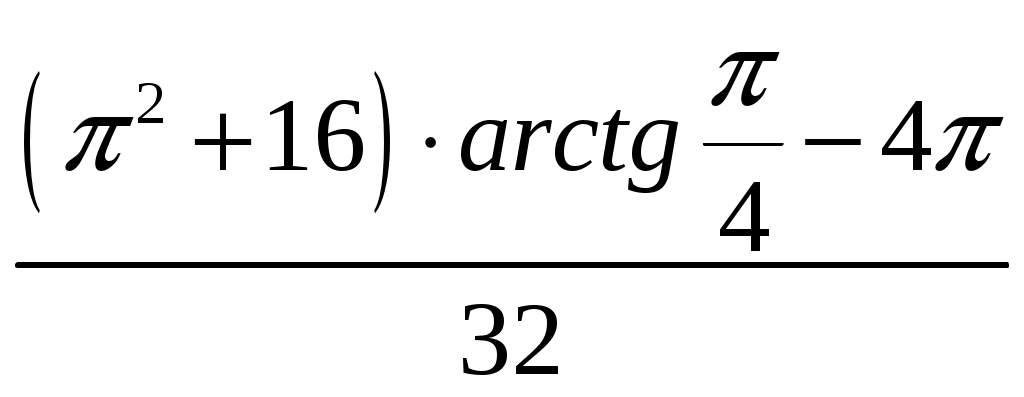
4. Вычислить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной гиперболой , осью OY и прямыми и . Построить чертеж.

Решение.

Выполним в плоскости Оху чертеж области, ограниченной указанными линиями, рис.



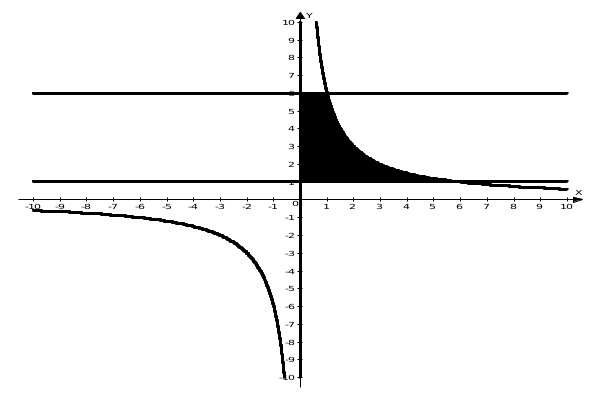
Объем тела вращения вокруг оси Оу можно вычислить по формуле:

.

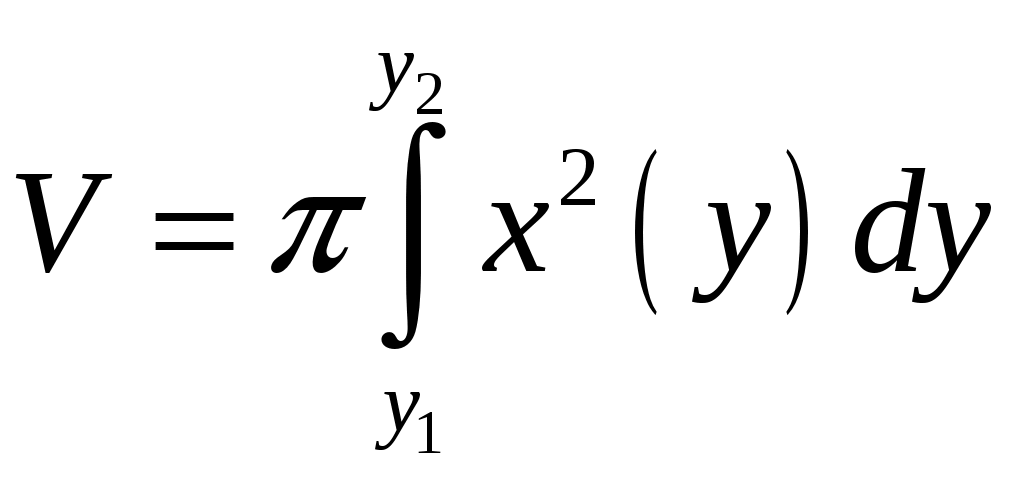Пределы интегрирования будут: .

Находим: .

Получаем:



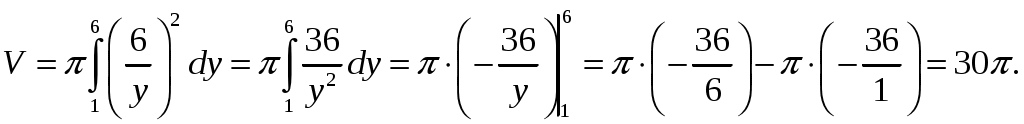
Ответ: ед. куб.

Смотрите также файлы