Файл: Московский университет им. С. Ю. Витте Рейтинговая работа Дискретная математика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 111
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Московский университет им. С.Ю. Витте
Рейтинговая работа
Дискретная математика
Вариант 1
1. Выполнение операций над множествами
Задание 1. Построить выражения над множествами (круг), (квадрат) и (треугольник), которым соответствуют заштрихованные области на заданных диаграммах Эйлера-Венна.
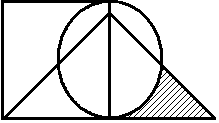
Решение:
Заштрихованной части треугольника соответствует та часть треугольника, которая не имеет общих элементов ни с кругом ни с квадратом. Таким образом, заштрихованной части соответствует выражение:
− ∪
Ответ: − ∪
Задание 2. Упростить выражение ∩ ∩ ∪ ∪ ∩ с применением тождеств алгебры множеств. Решение:
дистрибутивный закон = 
дистрибутивный закон = 
закон дополнительности = 
закон идентичности = = ∩ ∩
∩ ∪ ∩ = дистрибутивный закон = = ∩ ∩
∩ ∪ ∩ ∩ ∩ = закон дополнительности = = ∅ ∩ ∩ ∪ ∩ ∅ ∩ = закон идентичности = ∅ ∪ ∅ = ∅
Ответ: ∩ ∩ ∪ ∪ ∩ = ∅ 2. Выполнение операций алгебры логики
Задание 1. Представить в СДНФ функцию
Построим таблицу истинности для заданной функции + $%, $&, $) :
| $% | $& | $) | | $% + $& | $% + $& $) | | $% + $& $) | + |
| 0 | 0 | 0 | 1 | 1 | 0 | | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
Для нахождения СДНФ нужно из таблицы истинности выделить лишь те строки, результат которых равен 1. Для данной функции набор строк будет следующим:
-
$%
$&
$)
+
1
1
0
1
Далее, для каждой строки выписываем конъюнкцию всех переменных по следующему алгоритму: если значение переменной в данной строке равно 1, то в конъюнкцию записываем саму переменную, а если равно 0, то – отрицание этой переменной. После этого все конъюнкции связываем в дизъюнкцию. В результате, совершенная дизъюнктивно-нормальная форма (СДНФ) нашей функции равна:
$%$&
Ответ:
↓ $) = $%$&Задание 2. Пусть даны высказывания = "инфляция − высокая" и
= "снижается эффективность производства". Записать в словесной форме высказывание 5 = → .
Решение:
В словесной форме импликация → читается «если , то »
Таким образом, высказывание из условий задачи записывается так:
Если инфляция высокая, то снижается эффективность производства
-
Решение задач теории графов.
Задание 1. Задана таблица смежности неориентированного графа.
Определить число петель в данном графе.
| | 7% | 7& | 7) | 78 | 79 | 7: |
| 7% | 1 | 1 | 1 | 1 | 1 | 1 |
| 7& | 1 | 1 | 1 | 1 | 1 | 0 |
| 7) | 1 | 1 | 1 | 1 | 0 | 0 |
| 78 | 1 | 1 | 1 | 0 | 0 | 0 |
| 79 | 1 | 1 | 0 | 0 | 0 | 0 |
| 7: | 1 | 0 | 0 | 0 | 0 | 0 |
Решение:
Данная таблица смежности имеет три единицы на главной диагонали, значит, число петель в данном графе равно трем.
Задание 2. Построить матрицу инцидентности для графа, изображенного на рисунке.
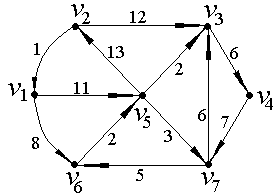
| Решение: | |
| Матрицей инцидентности орграфа ; называется < × > матрица ?@ABC у которой элементы равны: 1, если вершина 7A является концом дуги $B @AB = D −1, если вершина 7A является началом дуги $B 0, если вершина 7A является концом дуги ребру $B Пронумеруем ребра заданного графа: | ; = |
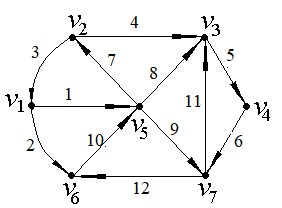
| −1 J 0 I 0 I ; = I 0 I 1 I 0 H 0 | −1 0 0 0 0 1 0 | 1 −1 0 0 0 0 0 | 0 −1 1 0 0 0 0 | 0 0 −1 1 0 0 0 | 0 0 0 −1 0 0 1 | 0 1 0 0 −1 0 0 | 0 0 1 0 −1 0 0 | 0 0 0 0 −1 0 1 | 0 0 0 0 1 −1 0 | 0 0 1 0 0 0 −1 | 0 0 M 0 LL 0 L
|
-
Комбинаторика. Применение графовых моделей.
Задание 1. Определить кратчайший путь из одной вершины графа в другую, изображенного на рисунке.
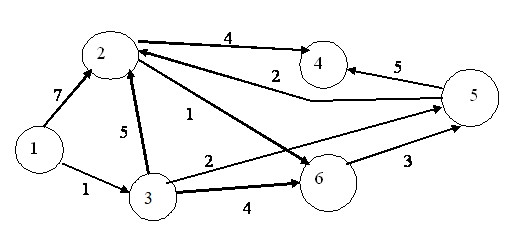
Решение:
Найдем кратчайшие пути из вершины 1 в остальные вершины графа по алгоритму Дейкстры.
Присваиваем вершине 1 метку 0. Остальным вершинам метку ∞ .
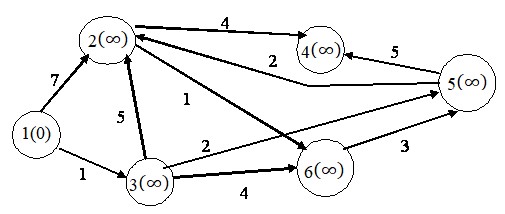
Первый шаг. Минимальную метку имеет вершина 1. Из нее можно попасть в вершины 2 и 3.
Первый по очереди сосед вершины 1 − вершина 3, потому что длина пути до нее минимальна. Длина пути в нее через вершину 1 равна сумме значения метки 1 и длины ребра, идущего из 1 в 3, то есть 0 + 1 = 1. Это меньше текущей метки вершины 3, бесконечности, поэтому новая метка вершины 3 равна 1.
Аналогичную операцию проделываем с вершиной 2.
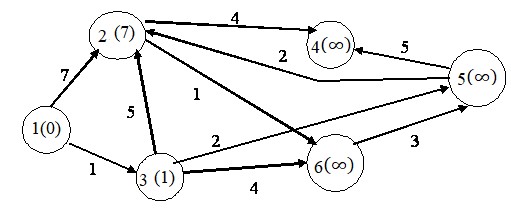
Все вершины, в которые можно попасть из вершины 1, проверены.
Отметим, что эта вершина посещена.
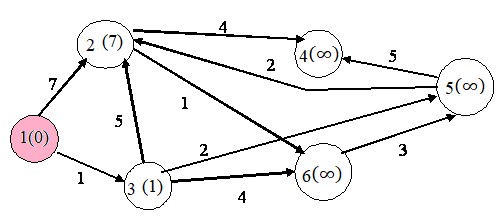
Второй шаг. Шаг алгоритма повторяется. Снова находим непосещенную вершину с минимальной меткой. Это вершина 3. Снова пытаемся уменьшить метки вершин, в которые можно попасть из вершины 3, а затем помечаем вершину 3 посещенной.
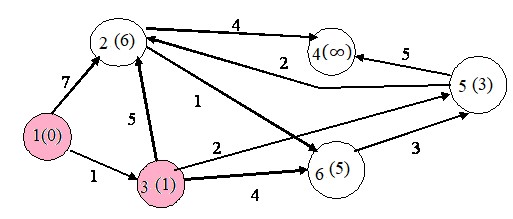
Третий шаг. Снова находим непосещенную вершину с минимальной
меткой. Это вершина 5. Работаем с ней:
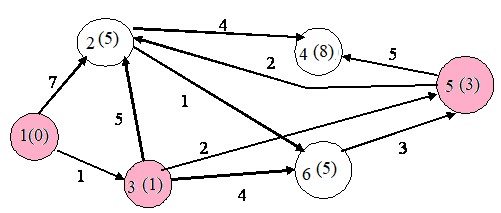
Следующим шагом выбираем вершину 2:
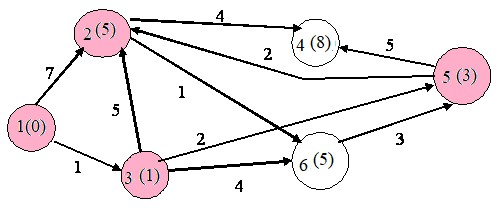
Следующим шагом выбираем вершину 6:
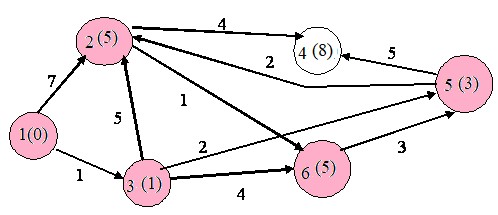
Алгоритм закончен.
Восстанавливая пути, получаем:
Кратчайший путь из вершины 1 в вершину 2: 5 1 → 3 → 5 → 2
Кратчайший путь из вершины 1 в вершину 3: 1 1 → 3
Кратчайший путь из вершины 1 в вершину 4: 8 1 → 3 → 5 → 4
Кратчайший путь из вершины 1 в вершину 5: 3 1 → 3 → 5 Кратчайший путь из вершины 1 в вершину 6: 5 1 → 3 → 6
Задание 2. Найдите разложение полинома 2$ − V 8
Решение:
Найдем искомое разложение при помощи треугольника Паскаля. По нему биномиальные коэффициенты для < = 4 равны 1,4,6,4,1. Таким образом, по биномиальной формуле имеем:
2$ − V 8 = 2$ 8 + 4 2$ ) −V + 6 2$ & −V & + 4 2$ −V ) +
+ −V 8 = 16$8 − 32$)V + 24$&V& − 8$V) + V8