ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 104
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа по курсу «Дискретная математика»
Вариант 9
9. Используя правила де Моргана, получить ДНФ и упростить ее
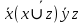
Решение:
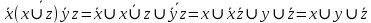
19. Даны две функции f1(x, y), f2(x, y, z). Требуется:
а) для функции f1(x, y) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. Упростить, если возможно, СДНФ.
б) для функции f2(x, y, z) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. По карте Карно получить минимальную ДНФ, нарисовать эквивалентную РКС.
в) составить таблицу Поста для системы функций f1(x, y), f2(x, y, z), проверить полноту системы и выбрать базисы, если она полная.
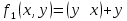
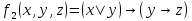
Решение:
а) составим таблицу истинности для функции
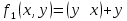
| x | y | 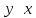 | 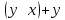 | СДНФ | СКНФ |
| 0 | 0 | 1 | 1 |  | |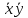
| 0 | 1 | 0 | 1 |  | |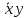
| 1 | 0 | 0 | 0 | |  |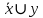
| 1 | 1 | 1 | 0 | |  |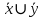
СДНФ – строится на наборах, на которых функция принимает значение 1
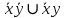
СКНФ – строится на наборах, на которых функция принимает значение 0
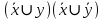
Минимизированная ДНФ
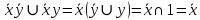
Полином Жегалкина
Для n=2 Р(х,у)=а0+а1х+а2у+а3ху
f(0,0)=P(0,0)=1= а0+а1*0+а2*0+а3*0= а0, получим а0=1
f(0,1)=P(0,1)=1= а0+а1*0+а2*1+а3*0= 1+а2= 1, получим а2=0
f(1,0)=P(1,0)=0= а0+а1*1+а2*0+а3*0= 1+а1= 0, получим а1=1
f(1,1)=P(1,1)=0= а0+а1*1+а2*1+а3*1= 1+1+а3= 0, получим а3=0
Р(х,у)=1+х – полином Жегалкина
б) составим таблицу истинности для функции
| x | у | z | 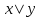 | 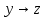 | 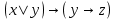 | СДНФ | СКНФ |
| 0 | 0 | 0 | 1 | 1 | 1 |  | |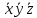
| 0 | 0 | 1 | 1 | 1 | 1 |  | |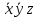
| 0 | 1 | 0 | 1 | 0 | 0 | |  |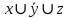
| 0 | 1 | 1 | 1 | 1 | 1 |  | |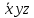
| 1 | 0 | 0 | 1 | 1 | 1 |  | |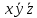
| 1 | 0 | 1 | 1 | 1 | 1 |  | |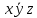
| 1 | 1 | 0 | 0 | 0 | 1 |  | |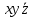
| 1 | 1 | 1 | 0 | 1 | 1 |  | |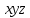
СДНФ – строится на наборах, на которых функция принимает значение 1
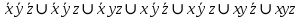
СКНФ – строится на наборах, на которых функция принимает значение 0
Минимизированная ДНФ
=
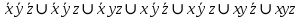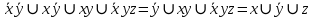
Полином Жегалкина
Для n=3 Р(х,у,z)=а0+а1х+а2у+а3z+а4хy+а5уz+а6xz+ а7xyz
f(0,0,0)=P(0,0,0)= а0=1, получим а0=1
f(0,0,1)=P(0,0,1)= а0 +а3z= 1 +а3= 1 , получим а3=0
f(0,1,0)=P(0,1,0)= а0 +а2y= 1 +а2= 0 , получим а2=1
f(0,1,1)=P(0,1,1)= а0+а2у+а3z+а5уz=1+1+ а5 = 1 , получим а5=1
f(1,0,0)=P(1,0,0)= а0 +а1x= 1 +а1= 1 , получим а1=0
f(1,0,1)=P(1,0,1)= а0+а1х+а3z+а6xz = 1+ а6= 1 , получим а6=0
f(1,1,0)=P(1,1,0)= а0+а1х+а2у+а4хy=1+1+ а4 = 1 , получим а4=0
f(1,1,1)=P(1,1,1)= а0+а1+а2+а3+а4+а5+а6+а7 = 1+1+1+1+1+а7 = 1 , получим а7=0
Р(х,у,z)=1+y+xy+yz+xyz– полином Жегалкина
Найдем минимизированную ДНФ с помощью карт Карно
Область 1:
 yzx | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
К1: х
Область 2:
| yz x | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
К2:
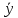
Область 3:
 yzx | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
К3:
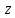
Минимизированная ДНФ:
Построим РКС
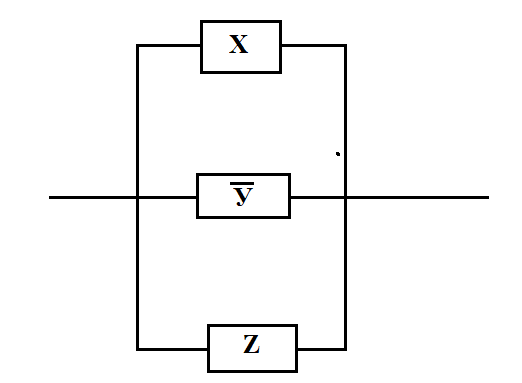
в) таблицы Поста
для функции
Класс T0
Функция принадлежит классу T0, если на нулевом наборе она сохраняет 0.
На нулевом наборе значение функции f(0,0)=1, поэтому функция не принадлежит классу T0.
Класс T1
Функция принадлежит классу T1, если на единичном наборе она сохраняет 1. На единичном наборе значение функции f(1,1)=0 поэтому функция не принадлежит классу T1.
Класс L
Функция принадлежит классу линейных функций (L), если её полином Жегалкина не содержит произведений. Полином Жегалкина функции:
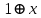не содержит произведений, поэтому функция принадлежит классу L.Класс M
Функция принадлежит классу монотонных функций (M), если для любой пары наборов α и β таких, что α ≤ β, выполняется условие f(α) ≤ f(β).
Сравним соседние наборы по первой переменной
Сравним значения {1} и {1}: условие монотонности выполнено.
Сравним значения {0} и {0}: условие монотонности выполнено
Сравним соседние наборы по второй переменной
Сравним значения {1,1} и {0,0}: условие монотонности нарушено
Таким образом функция не принадлежит классу M.
Класс S
Функция принадлежит классу самодвойственных функций (S), если на противоположных наборах она принимает противоположные значения. Проверим значения на наборах {0, 0} и {1, 1}: 1 и 0 противоположны.
Проверим значения на наборах {0, 1} и {1, 0}: 1 и 0 противоположны Поэтому функция принадлежит классу S
Построим таблицу
| | T0 | T1 | L | M | S |
 | - | - | + | - | + |
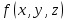для функции
Класс T0
Функция принадлежит классу T0, если на нулевом наборе она сохраняет 0.
На нулевом наборе значение функции f(0,0,0)=1, поэтому функция не принадлежит классу T0.
Класс T1
Функция принадлежит классу T1, если на единичном наборе она сохраняет 1. На единичном наборе значение функции f(1,1,1)=1 поэтому функция принадлежит классу T1.
Класс L
Функция принадлежит классу линейных функций (L), если её полином Жегалкина не содержит произведений. Полином Жегалкина функции: Р(х,у,z)=1+y+xy+yz+xyz содержит произведения, поэтому функция не принадлежит классу L.
Класс M
Функция принадлежит классу монотонных функций (M), если для любой пары наборов α и β таких, что α ≤ β, выполняется условие f(α) ≤ f(β).
Сравним соседние наборы по первой переменной
Сравним значения {1} и {1}: условие монотонности выполнено.
Сравним значения {0} и {1}: условие монотонности выполнено
Сравним значения {1} и {1}: условие монотонности выполнено
Сравним значения {1} и {1}: условие монотонности выполнено
Сравним соседние наборы по второй переменной
Сравним значения {1,1} и {0,1}: условие монотонности нарушено
Таким образом функция не принадлежит классу M.
Класс S
Функция принадлежит классу самодвойственных функций (S), если на противоположных наборах она принимает противоположные значения. Проверим значения на наборах {0, 0, 0} и {1, 1, 1}: 1 и 1 совпадают. Поэтому функция не принадлежит классу S
Построим таблицу
| | T0 | T1 | L | M | S |
| | - | + | - | - | - |
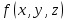