Файл: Задача 107 Два груза m 1 1кг и m 2.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 09.12.2023

Просмотров: 201

Скачиваний: 11

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ЗАДАЧА № 107



Два груза m1=1кг и m2=0,5 кг связаны легким шнуром, перекинутым через блок (рис.). Блок радиусом R=10 см вращается с угловым ускорением ε=20 рад/с2. Найти массу блока, если она равномерно распределена по его ободу.


Дано:

  • R = 0,1 м ,

  • ,

  • ,


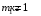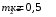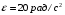
Найти:




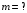
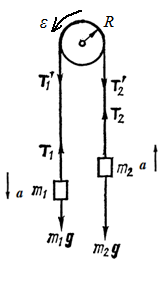
Решение:

При решении задачи применим основные законы поступательного движения.

На каждый из движущихся грузов действуют две силы: сила тяжести 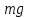, направленная вниз, и сила Т натяжения нити, направленная вверх.


Груз 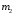по условию задачи в 2 раза меньше по массе чем груз 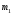. Следовательно груз 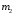будет двигаться вверх с ускорением 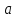. А груз 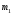будет двигаться вниз с ускорением .

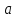Так как вектор ускорения 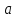груза 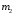направлен вверх, то:

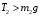- пусть будет формула A

Равнодействующая этих сил вызывает равноускоренное движение и, по второму закону Ньютона, равна:

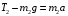- пусть будет формула B

Из формулы B получаем:

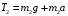- пусть будет формула
C

Вектор ускорения груза направлен вниз, следовательно: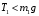

- пусть будет формула D

Равнодействующая этих сил вызывает равноускоренное движение и, по второму закону Ньютона, равна:

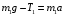- пусть будет формула Q

Из формулы Q получаем:

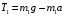- пусть будет формула Z

Согласно основному закону динамики вращательного движения, вращающий момент 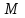, приложенный к блоку, равен произведению момента инерции 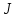блока на его угловое ускорение :

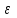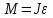- пусть будет формула U

Определим вращающий момент. Силы натяжения нитей действуют не только на грузы, но и на блок. По третьему закону Ньютона, силы 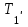и 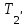, приложенные к ободу блока, равны соответственно силам 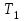и 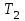, но по направлению им противоположны. При движении грузов блок ускоренно вращается против часовой стрелке. Следовательно, .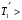

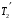Вращающий момент, приложенный к блоку, равен произведению разности этих сил на плечо, равное радиусу блока R, т.е.:

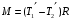- пусть будет формула O

Момент инерции блока в виде колеса, масса которого равномерно распределена по ободу:

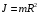- пусть будет формула F

Угловое ускорение блока связано с линейным ускорением грузов соотношением:

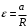- пусть будет формула K

Подставим в формулу
U формулы O , F и K:

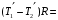
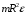- пусть будет формула W

Из формулы W получаем:

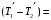
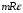- пусть будет формула L

Так как 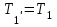и 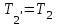, то подставим формулы C и Z в формулу L: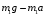

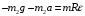- пусть будет формула N

Преобразуем формулу N к виду:



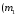
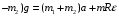
или с учетом формулы K:



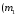
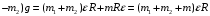
- пусть будет формула I

Из формулы I выразим массу блока и найдем её:



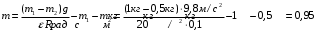
Ответ: Масса блока (m) = 0,95 кг

Смотрите также файлы