Файл: Контрольная работа по статистике 13. 03. 02. код направления подготовки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования РФ
федеральное государственное бюджетное образовательное учреждение высшего образования
«Вологодский государственный университет»
Институт машиностроения, энергетики и транспорта
(наименование института)
Кафедра электрооборудования
(наименование кафедры)
Дисциплина: «Прикладная математика в энергетике»
Наименование темы: «Контрольная работа по статистике»
| _____13.03.02_______. код направления подготовки/ специальности | __44.02__. код выпускающей кафедры | ______2______ регистрационный номер по журналу | ____2______ код формы обучения | _____2023_____ год |
| Руководитель | доц. Иванова С.В. |
| (уч. степень, звание, должность. Ф.И.О) | |
| Выполнил (а) студент | Бусырев Егор Витальевич |
| (Ф.И.О) | |
| Группа, курс | 5Б13 ЭС-21; 2 курс |
| Дата сдачи | |
| Дата защиты | |
| Оценка по защите | |
| (подпись преподавателя) |
Вологда
2022 г.
5 КОНТРОЛЬНАЯ РАБОТА
Задача Суточное потребление электроэнергии на рабочем месте в цехе может быть рассмотрено как случайная величина Х, распределенная по нормальному закону. Было произведено 40 измерений этой величины (табл. 5.1).
1.1 Провести группировку данных, разбив варианты на 5 интервалов.
1.2 Для сгруппированного ряда построить гистограмму частот.
2.1 Найти выборочную среднюю
, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.
2.2 Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95.
3.1 При уровне значимости α = 0,05 проверить утверждение энергослужб предприятия, что среднесуточное потребление электроэнергии на рабочем месте равно a (табл. 5.2).
3.2 После переналадки оборудования, произведенной с целью уменьшения потребления электроэнергии, были проведены новые измерения, и получена выборка объема 10 (табл. 5.3.). При уровне значимости α проверить, является ли статистически обоснованным утверждение производителя об уменьшении среднего потребления электроэнергии.
Таблица 5.1
| N1=0 , N2=2 | |||||||
| i | xi | i | xi | i | xi | i | xi |
| 1 | 3,06+2=5,06 | 11 | 4,52+2=6,52 | 21 | 5,22+2=7,22 | 31 | 5,91+2=7,91 |
| 2 | 3,45+2=5,45 | 12 | 4,64+2=6,64 | 22 | 5,27+2=7,27 | 32 | 5,91+2=7,91 |
| 3 | 3,72+2=5,72 | 13 | 4,65+2=6,65 | 23 | 5,29+2=7,29 | 33 | 6,24+2=8,24 |
| 4 | 3,77+2=5,77 | 14 | 4,75+2=6,75 | 24 | 5,44+2=7,44 | 34 | 6,25+2=8,25 |
| 5 | 3,88+2=5,88 | 15 | 4,78+2=6,78 | 25 | 5,63+2=7,63 | 35 | 6,27+2=8,27 |
| 6 | 4,11+2=6,11 | 16 | 4,88+2=6,88 | 26 | 5,65+2=7,65 | 36 | 6,32+2=8,32 |
| 7 | 4,15+2=6,15 | 17 | 5,08+2=7,08 | 27 | 5,68+2=7,68 | 37 | 6,40+2=8,40 |
| 8 | 4,24+2=6,24 | 18 | 5,09+2=7,09 | 28 | 5,75+2=7,75 | 38 | 6,51+2=8,51 |
| 9 | 4,28+2=6,28 | 19 | 5,18+2=7,18 | 29 | 5,80+2=7,80 | 39 | 6,78+2=8,78 |
| 10 | 4,49+2=6,49 | 20 | 5,22+2=7,22 | 30 | 5,88+2=7,88 | 40 | 7,05+2=9,05 |
Таблица 5.2
| N1 | 0 |
| а | 5+2=7 |
Таблица 5.3
| N1=0 , N2=2 | |||
| i | xi | i | xi |
| 1 | 2,47+2=4,47 | 6 | 4,59+2=6,59 |
| 2 | 3,85+2=5,85 | 7 | 4,79+2=6,79 |
| 3 | 4,34+2=6,34 | 8 | 5,16+2=7,16 |
| 4 | 4,35+2=6,35 | 9 | 5,42+2=7,42 |
| 5 | 4,47+2=6,47 | 10 | 5,88+2=7,88 |
Решение
-
Проведем группировку исходных данных, т.е. разобьем варианты на отдельные интервалы. Найдем разность между наибольшим и наименьшим значениями признака: xmax – xmin = 9,05 – 5,06 = 3,99. Тогда при разбивке на 5 интервалов длина интервала составит h = 3,99/5 = 0,798 ≈ 0,8. Для упрощения дальнейших расчетов выберем границы интервалов таким образом, чтобы середины интервалов являлись как можно более «круглыми» числами (с наименьшим числом знаков после запятой). Получим табл. 5.4.
Таблица 5.4
| № | Интервал | Середина интервала | Частота ni | Относительная частота  |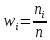
| 1 | 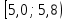 | 5,04 | 4 | 0,1 |
| 2 | 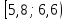 | 6,2 | 8 | 0,2 |
| 3 | 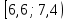 | 7 | 12 | 0,3 |
| 4 | 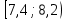 | 7,8 | 9 | 0,225 |
| 5 | 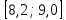 | 8,6 | 7 | 0,175 |
| Σ | 40 | 1 | ||
1.2 Построим для сгруппированного ряда гистограмму частот.
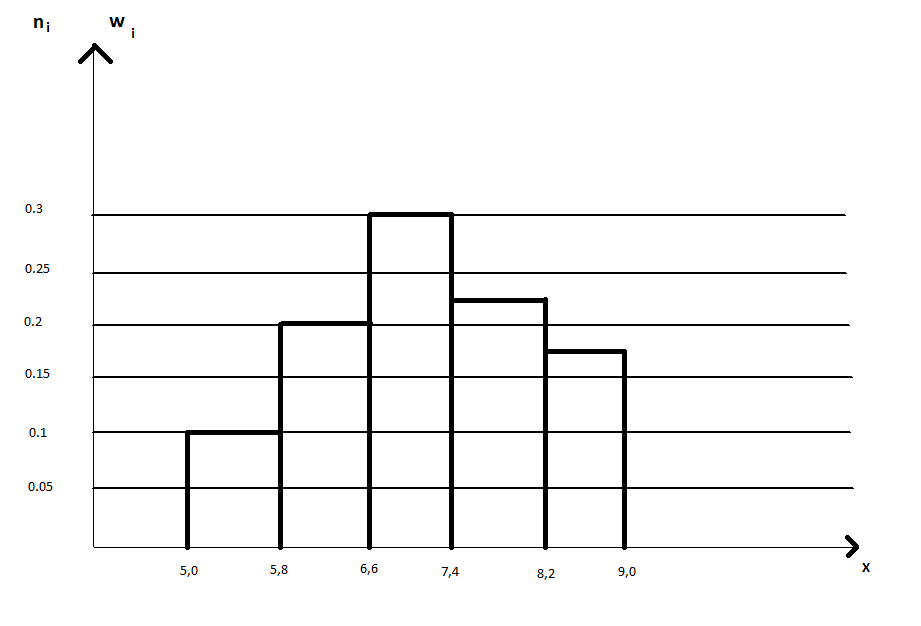
Рис. 1.
2.1 Найдем выборочную среднюю
:
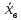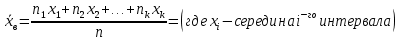
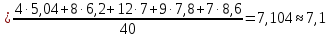
Найдем выборочную дисперсию Dв
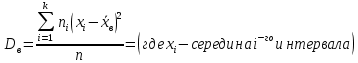
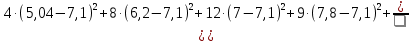
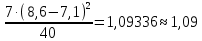
Найдем исправленную выборочную дисперсию:
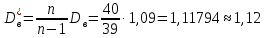
Найдем исправленное выборочное среднеквадратическое отклонение случайной величины Х
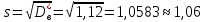
2.2 Построим доверительный интервал для генеральной средней с уровнем доверительной вероятности γ = 0,95. Так как значение генеральной дисперсии неизвестно, воспользуемся формулой
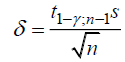. Найдем значение t1–γ, n–1 = t0,05;39 по таблице критических точек распределения Стьюдента при уровне вероятности α = 0,05 и числе степеней свободы k = n – 1 = 39. Получаем t0,05;39 = 2,02. Далее находим точность оценки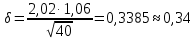 
Доверительный интервал для генеральной средней имеет вид
Подставляя значения, получаем, что с вероятностью 0,95 выполнено: x ∈ (6,76; 7,44)
Построим доверительный интервал для генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95.
Найдем значение
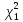по таблице критических точек распределения χ2 при уровне вероятности (1 + γ) / 2 = 0,975 и числе степеней свободы k = n – 1 = 39. Получаем 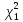= 22,9, следовательно, χ1 = 4,8. Найдем значение 
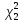по таблице критических точек распределения χ2 при уровне вероятности (1 – γ) / 2 = 0,025 и числе степеней свободы
k = n – 1 = 39. Получаем
= 58,1, следовательно, χ2 = 7,6. Доверительный интервал для генерального среднеквадратического отклонения имеет вид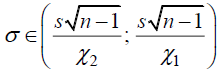 
. Подставляя значения, получаем, что с вероятностью 0,95 выполнено
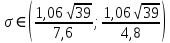или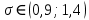 
3.1 При уровне значимости α = 0,05 проверим утверждение, что среднее значение величины Х соответствует проектному значению a = 7. Так как выборка имеет большой объем (n = 40 > 30), то для проверки нулевой гипотезы Н0:
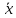a в качестве критерия проверки можно принять случайную величину U. При этом в качестве генерального среднеквадратического отклонения σ можно принять выборочное значение s.Вычислим наблюдаемое значение критерия
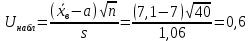
Конкурирующей является гипотеза Н1: x a , поэтому критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – α)/2 = 0,475. Получаем Uкр=1,96. Так как |Uнабл| < Uкр, то нет оснований отвергнуть нулевую гипотезу. Следовательно, утверждение, что среднее значение входного параметра Х соответствует проектному значению, является статистически обоснованным.
3.2 Для первой выборки объема n1 = 40 были получены значения
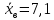; s1 = 1,06. Найдем выборочную среднюю и выборочное среднеквадратическое отклонение для второй выборки объема n2 = 10 (табл. 5.3).Найдем выборочную среднюю:
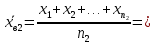
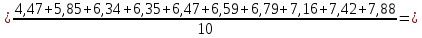
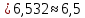
Найдем выборочную дисперсию:
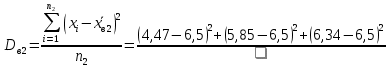
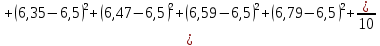
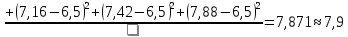
Найдем исправленную выборочную дисперсию по формуле
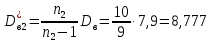
Найдем исправленное выборочное среднеквадратическое отклонение случайной величины