Файл: Пример в механизме строгального станка, общее количество звеньев.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Образец выполнения задания
Пример: в механизме строгального станка, общее количество звеньев k= 6, а число подвижных звеньев n = 5.
Дадим названия звеньям по характеру их движения.
Таблица 1.1 – Обозначение звеньев механизма
| Кинематическая схема | Звенья механизма |
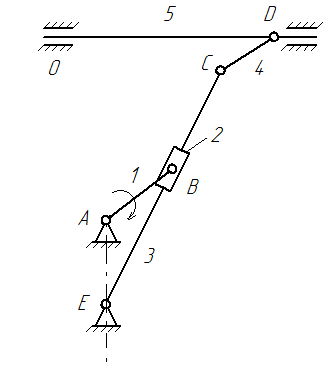 | 1 – кривошип 2 – ползун 3 – кулиса 4 – шатун 5 – ползун 0 – стойка – неподвижное звено |
Входным звеном является кривошип 1, совершающий вращательное движение, выходным звеном – ползун 5, совершающий поступательное движение.
Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой. В зависимости от характера соприкосновения звеньев кинематическая пара может быть низшей или высшей.
Характеристику кинематических пар сведем в таблицу 1.2.
Таблица 1.2 – Характеристика кинематических пар
| Обоз-наче-ние пары | Звенья, образующие пару | Подвижность пары (одно- или двухподвижная), класс пары | Разновидность пары: высшая или низшая; вращательная или поступательная |
| А01 | Стойка – кривошип | Одноподвижная, класс 5 (Р5) | Низшая, вращательная |
| B12 | Кривошип – ползун | Одноподвижная, класс 5 (Р5) | Низшая, вращательная |
| B23 | Ползун – кулиса | Одноподвижная, класс 5 (Р5) | Низшая, поступательная |
| C34 | Кулиса – шатун | Одноподвижная, класс 5 (Р5) | Низшая, вращательная |
| D45 | Шатун – ползун | Одноподвижная, класс 5 (Р5) | Низшая, вращательная |
| D50 | Ползун – стойка | Одноподвижная, класс 5 (Р5) | Низшая, поступательная |
| E30 | Кулиса – стойка | Одноподвижная, класс 5 (Р5) | Низшая, вращательная |
Число степеней свободы плоского механизма, т. е. число степеней свободы его подвижной кинематической цепи относительно стойки, определяется по формуле Чебышева:
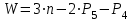,где n= 5 – число подвижных звеньев механизма;
p5= 7 – количество одноподвижных кинематических пар 5-го класса;
p4= 0 – количество двухподвижных кинематических пар 4-го класса.
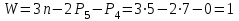.Разложим механизм на группы Ассура и определим их класс и порядок.
Характеристику групп Ассура и начального звена сведем в таблицу 1.3.
Таблица 1.3 – Характеристика групп Ассура
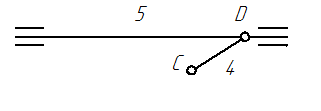 | Группа Ассура № 1 Класс – II Порядок – 2 |
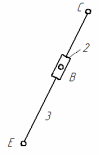 | Группа Ассура № 2 Класс – II Порядок – 2 |
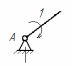 | Исходный механизм Класс – I |
Структурная формула образования механизма тогда запишется следующим образом:
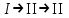, механизм II класса. Класс механизму присваивается по наивысшему классу группы Ассура.Если в механизме имеются пары четвертого класса, их следует заменить кинематической цепью, состоящей из пар пятого класса. При такой замене должно удовлетворяться условие: механизм, полученный после замены, должен обладать прежней степенью подвижности и сохранять относительные в рассматриваемом положении движения всех его звеньев.
На рис. 1 показаны примеры замены высших кинематических пар низшими парами.
Для образования заменяющего механизма любую из высших кинематических пар заменяют одним звеном и двумя низшими кинематическими парами.
Замену следует производить таким образом: в точке касания профилей к ним проводится нормаль, на которой находятся центры кривизны
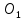
и
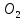кривых, образующих эти профили. Точки 
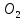и обозначают центры шарниров, которые затем соединяются условным звеном 3. Заменяющий механизм показан на схемах оранжевым цветом.Если один из соприкасающихся профилей представляет собой прямую, то центр кривизны этого профиля будет бесконечно удален и вращательная пара переходит в поступательную.
В случаях а и б замена производится на две вращательные пары
и 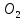и звено 3. В случаях в и г – на одну вращательную и одну поступательную низшие кинематические пары и условное звено.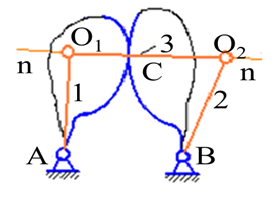
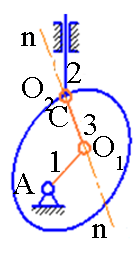
а б
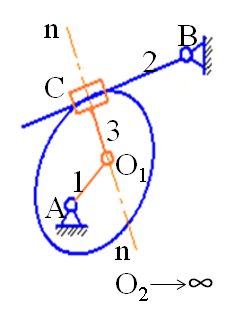
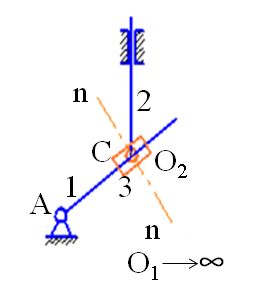
в г
Рис. 1. Замена высших кинематических пар низшими парами
Степень подвижности всех механизмов после замены не должна измениться.