Файл: Время выполнения На выполнение всей работы отводится 45 минут. Назначение работы Определить уровень овладения предметных результатов у учащихся 7 класса по итогам усвоения программы по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 51
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Промежуточная аттестацияПредмет: геометрия, 7 классУсловия проведения процедуры промежуточной аттестации: Работа проводится в классе, задания выполняются на двойном листочке в клеткуВремя выполнения:На выполнение всей работы отводится 45 минут.Назначение работы:Определить уровень овладения предметных результатов у учащихся 7 класса по итогам усвоения программы по предмету «Геометрия».Структура и содержание работы:Работа проводится в форме тестирования, состоит из 5 заданий:№1 Сумма углов треугольника№2 Свойство углов равнобедренного треугольника.№3 Свойства углов при параллельности прямых№4 Свойство биссектрисы и высоты треугольника.№5 Задача на доказательствоОбобщенный план:
Отметочная шкала:Задания 1-5 - 1 баллВыставление отметки:Предметные и метапредметные результаты оцениваются одной единой отметкой«5» - 5 баллов «4» - 4 балла«3» - 3 балла«2» - до 3 балловДемоверсия
. На плоскости даны четыре прямые. Известно, что ∠1 = 123°, ∠2 = 57°, ∠4 = 146°. Найдите ∠3. 1) 43 2) 34 3) 57 4) 1464. В треугольнике АВС углы А и С равны 30° и 70° соответственно. Найдите угол между высотой ВН и биссектрисой BD.1) 20 2) 30 3) 10 4) 705. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны. Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.2 вариант1. В треугольнике один угол в 2 раза больше второго и на 40° больше третьего угла. Найдите больший угол треугольника. 1) 44 2) 88 3) 40 4)802. В треугольнике АВС известно, что АВ = ВС, ∠АВС = 38° . Найдите угол ВАС. 1) 71 2) 38 3) 62 4) 173
. Прямые
m и n параллельны. Найдите ∠1, если ∠2 = 41°, ∠3 = 68°. 1)71 2) 41 3) 68 4) 1094. В треугольнике АВС углы А и С равны 60° и 80° соответственно. Найдите угол между высотой ВН и биссектрисой BD.1) 60 2) 80 3) 140 4) 305. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны. Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВD равен треугольнику СВЕ. Ответы
| № задания | Контролируемые элементы содержания (предметные результаты) | Связь с УУД (познавательные результаты) | Тип | Балл |
| 1 | Применение для решения задач геометрические факты, условия их применения которых заданы в явной форме | Перевод информации из графического представления в текстовое и наоборот | Б | 1 балл |
| 2 | Применение для решения задач геометрические факты, условия их применения которых заданы в явной форме | Перевод информации из графического представления в текстовое и наоборот | Б | 1 балл |
| 3 | Извлечение информации о геометрических фигурах, представленную на чертеже в явном виде | Перевод информации из графического представления в текстовое | Б | 1 балл |
| 4 | Применение для решения задач геометрические факты, условия их применения которых заданы в явной форме | Перевод информации из графического представления в текстовое и наоборот | Б | 1 балл |
| 5 | Доказательство геометрического утверждения | Построение доказательства | Б | 1 балл |
Отметочная шкала:Задания 1-5 - 1 баллВыставление отметки:Предметные и метапредметные результаты оцениваются одной единой отметкой«5» - 5 баллов «4» - 4 балла«3» - 3 балла«2» - до 3 балловДемоверсия
-
Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол.
-
В треугольнике АВС известно, что АВ = ВС, ∠АВС = 46° . Найдите угол ВСА. -
Н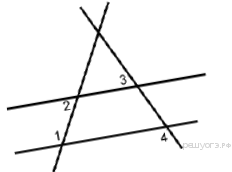 а плоскости даны четыре прямые. Известно, что ∠1 = 115°, ∠2 = 65°, ∠3 = 47°. Найдите ∠4.
-
В треугольнике АВС углы А и С равны 75° и 85° соответственно. Найдите угол между высотой ВН и биссектрисой BD. -
В треугольнике ABC угол B равен 36°, AB = BC, AD — биссектриса. Докажите, что треугольник AВD — равнобедренный.
. На плоскости даны четыре прямые. Известно, что ∠1 = 123°, ∠2 = 57°, ∠4 = 146°. Найдите ∠3. 1) 43 2) 34 3) 57 4) 1464. В треугольнике АВС углы А и С равны 30° и 70° соответственно. Найдите угол между высотой ВН и биссектрисой BD.1) 20 2) 30 3) 10 4) 705. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны. Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.2 вариант1. В треугольнике один угол в 2 раза больше второго и на 40° больше третьего угла. Найдите больший угол треугольника. 1) 44 2) 88 3) 40 4)802. В треугольнике АВС известно, что АВ = ВС, ∠АВС = 38° . Найдите угол ВАС. 1) 71 2) 38 3) 62 4) 173 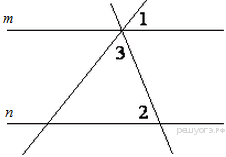. Прямые
m и n параллельны. Найдите ∠1, если ∠2 = 41°, ∠3 = 68°. 1)71 2) 41 3) 68 4) 1094. В треугольнике АВС углы А и С равны 60° и 80° соответственно. Найдите угол между высотой ВН и биссектрисой BD.1) 60 2) 80 3) 140 4) 305. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны. Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВD равен треугольнику СВЕ. Ответы
| № | 1 вариант | 2 вариант |
| 1 | 15° | 88° |
| 2 | 44° | 71° |
| 3 | 34° | 71° |
| 4 | 10° | 30° |
| 5 | Доказательство: BD=BE по условию, значит треугольник DBE равнобедренный. Следовательно, по свойству равнобедренного треугольника угол BDE равен углу BED.Угол ADB равен углу BEC как смежные равным углам BDE и BED соответственно. Треугольники ADB и CEB равны по двум сторонам и углу между ними (АВ=EC, BD=BE, угол ADB равен углу BEC). В равных треугольниках равны соответственные элементы, значит AB=BC. Треугольник АВС – равнобедренный. Что и требовалось доказать. | Доказательство: BD=BE по условию, значит треугольник DBE равнобедренный. Следовательно, по свойству равнобедренного треугольника угол BDE равен углу BED.Угол ADB равен углу BEC как смежные равным углам BDE и BED соответственно. Треугольники ADB и CEB равны по двум сторонам и углу между ними (АВ=EC, BD=BE, угол ADB равен углу BEC). Что и требовалось доказать. |