Добавлен: 11.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Бланк выполнения задания 2
| № п/п | Задача | Ответ | |||||||||||||||||
| 1. | Рассчитать наибольшее и наименьшее значения функции на заданном отрезке: | y=x3-3·x+1 Находим первую производную функции: y′=3·x2-3 Приравниваем ее к нулю 3·x2-3=0 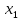 =-1 =-1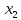 =1 =1Вычисляем значения функции на концах интервала f(-1)=3 f(1)=-1 f(0.5)=-0.375 f(2)=3 Ответ: fmin = -1, fmax = 3 | |||||||||||||||||
| 1) Найти первую производную и все критические точки: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| 2) Вычислить значения функции в критических точках: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| 3)Вычислить значения функции на концах промежутка: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| 4)Сравнить все полученные значения функции и выбрать среди них самое большое и самое малое: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| 2а. | Провести полное исследование и построить графики данных функций: | Построить график, используя полученные результаты | |||||||||||||||||
| Найти область определения функции, исследовать её поведение на границах этой области: | y= 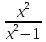 1)Найдем точки разрыва функции. x1=-1 x2=1 2)Четность или нечетность функции: y(-x)= 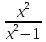 y(-x) = y(x), четная функция 3)Точки пересечения кривой с осями координат: Пересечение с осью 0Y: x=0, y=0 Пересечение с осью 0X: y=0  x1=0 x1=0 4)Находим интервалы возрастания и убывания: f(x)= 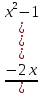 (производная ) (производная )Находим нули функции. Для этого приравниваем производную к нулю x=0 x1=0
5)Асимптоты кривой: Уравнения наклонных асимптот y = kx + b. По определению асимптоты: limx→∞ k·x+b-f(x) Находим коэффициент k= 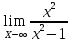 = =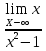 =∞ =∞Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует. 6)Исследование на экстремум: y(x)= 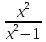 Найдем точки разрыва функции x1=-1 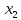 =1 =1Поскольку f(-x)=f(x), то функция является четной. 7)Найдем интервалы выпуклости и вогнутости функции: f(x)= 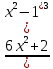 = 0 (производная) = 0 (производная)Для данного уравнения корней нет
| ||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки разрыва и классифицировать их с помощью односторонних пределов: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Исследовать периодичность, чётность (нечётность): | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти асимптоты: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки экстремума и интервалы монотонности: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки перегиба и интервалы выпуклости и вогнутости: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| 2б. | Провести полное исследование и построить графики данных функций: | Построить график, используя полученные результаты | |||||||||||||||||
| Найти область определения функции, исследовать её поведение на границах этой области: | y x lnx 1 1)Область определения функции. Точки разрыва функции: f(x)=ln(x), x>0 Для нашей функции: x+1>0 x=-1 2)Четность или нечетность функции: y(-x)=-x-ln(1-x) Функция общего вида 3)Точки пересечения кривой с осями координат: Пересечение с осью 0Y x=0, y=0 Пересечение с осью 0X y=0 x-ln(x+1)=0 x1=0 4)Асимптоты кривой: Находим коэффициент k: k= 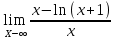 = =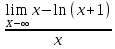 =1 =1Находим коэффициент b: b= 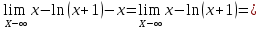 -∞ -∞Предел равен -∞, следовательно, наклонные асимптоты функции отсутствуют. 5) Находим интервалы возрастания и убывания. Первая производная. F(x)= 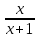 (производная) (производная)Находим нули функции. Для этого приравниваем производную к нулю: 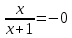 x=0 Откуда: x1=0 (-∞ ;0) (0; +∞) f'(x) < 0 f'(x) > 0 функция убывает функция возрастает 6)Найдем интервалы выпуклости и вогнутости функции. F(x)= 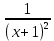 (производная) (производная)Находим корни уравнения. Для этого полученную функцию приравняем к нулю: 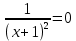 Для данного уравнения корней нет
| ||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки разрыва и классифицировать их с помощью односторонних пределов: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Исследовать периодичность, чётность (нечётность): | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти асимптоты: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки экстремума и интервалы монотонности: | |||||||||||||||||||
| Подробное решение: | |||||||||||||||||||
| Найти точки перегиба и интервалы выпуклости и вогнутости: | |||||||||||||||||||
| Подробное решение: |