Файл: Исследование типовых радиотехнических звеньев и структурные преобразования систем радиоавтоматики.doc

Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательноеучреждение высшего образованияТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМУПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)Кафедра радиотехнических систем (РТС)Контрольная работа № 1по дисциплине «Радиоавтоматика»Тема: Исследование типовых радиотехнических звеньеви структурные преобразования систем радиоавтоматики

	Выполнил	студент гр. з-140П5-4
		_______ Е. С. Дикусаренко
		«28» декабря 2022 г.
	Проверил	ст. преп. каф. ТОР
		__________ Д. Ю. Пелявин
		«__»_______ 2022 г.

2022

Задание 1

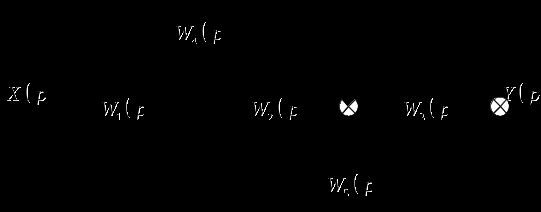
Определить передаточную функцию сложной системы радиоавтоматики, для чего произвести структурные преобразования.Рисунок 1 – Структурная схема системыТаблица 1 – Вид типовых радиотехнических звеньев

№
66

---

Таблица 2 – Параметры типовых радиотехнических звеньев

№
66	12	–	4	–	1	0,2	0,1	0,5	4	–	–	–	0,2

Решение

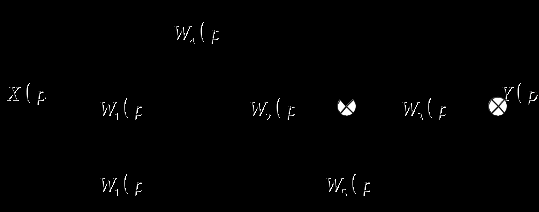
Последовательность преобразования структурной схемы (рис. 1) на основе правил структурных преобразований [1], представляется следующим алгоритмом: перенос узла ответвления через звено с передаточной функцией (рис. 2).После структурных преобразований системы РА определим передаточную функцию для системы и представим в виде аналитического выражения:Рисунок 2 – Преобразование структурной схемы исследуемой системы

---

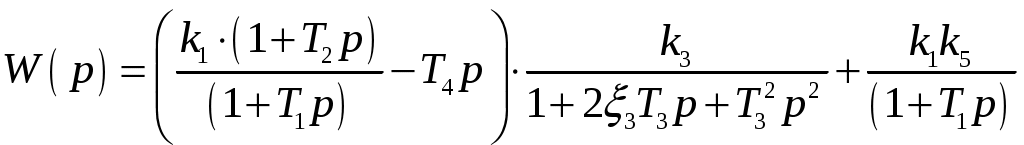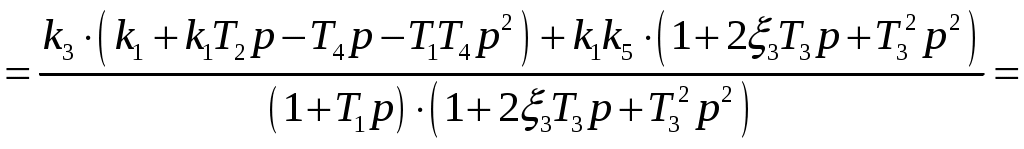
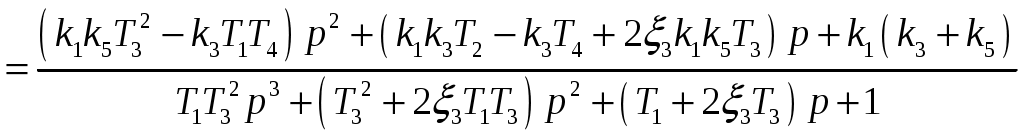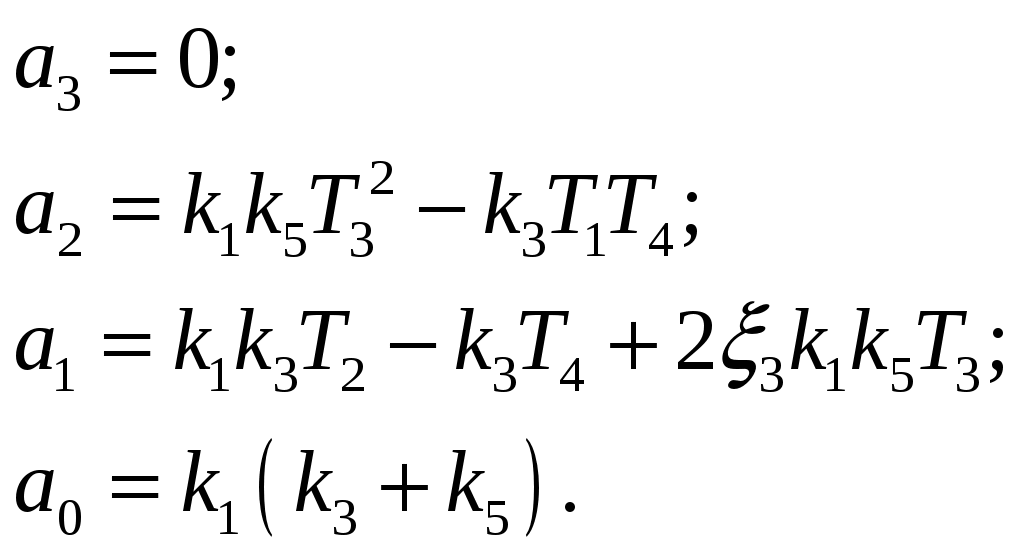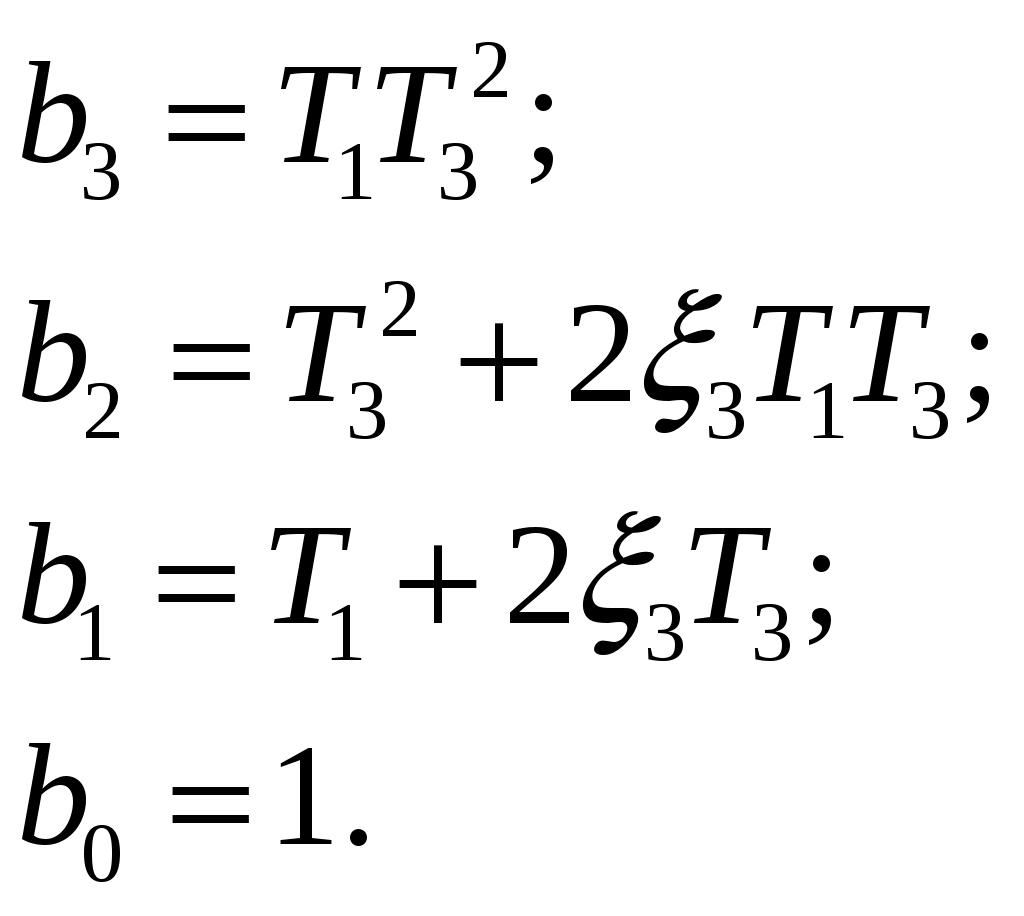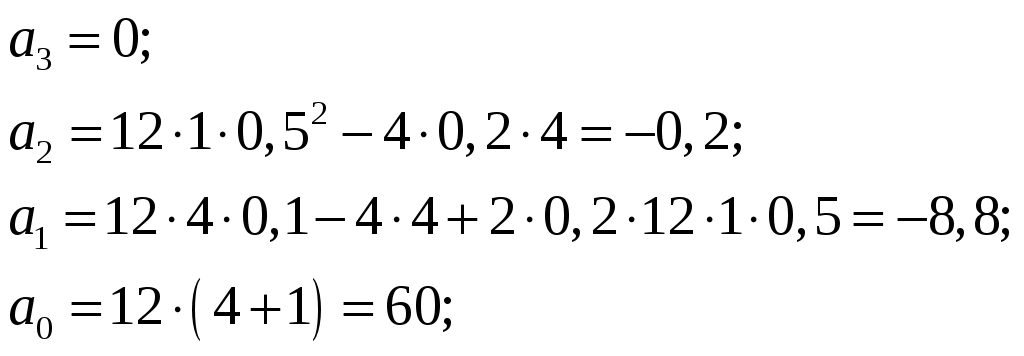
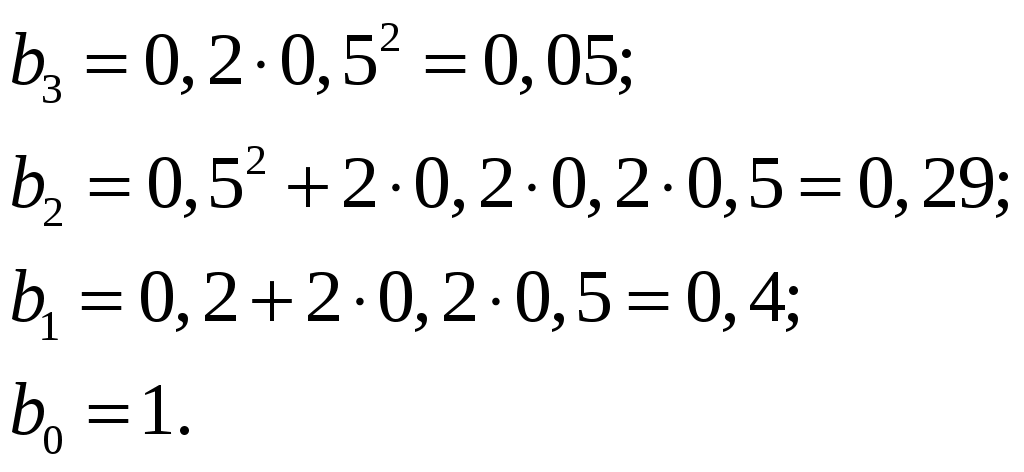
.Далее подставим значения звеньев структурной схемы из таблицы 1 и получим: ; .Далее, согласно заданию, представим полученные выражения числителя и знаменателя в виде полиномов: ,максимальная степень оператора Лапласа равна трём, а значит, полиномы, описывающие передаточные свойства системы, будут не выше третьего порядка: ; ,отсюда: и .Затем подставим значения элементов из таблицы 2 и получим:и Теперь передаточная функция будет выглядеть так: ,полученный результат запишем в форме: ; .В нашем случае: ; .

Задание 2

Построить линеаризованную ЛАЧХ и ЛФЧХ системы радиоавтоматики.Таблица 3 – Параметры передаточной функции

№	Передаточная функция
66		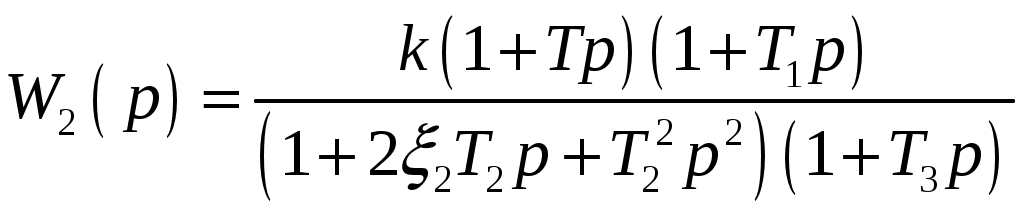30	0,2	0,1	0,2	0,2

---

Решение

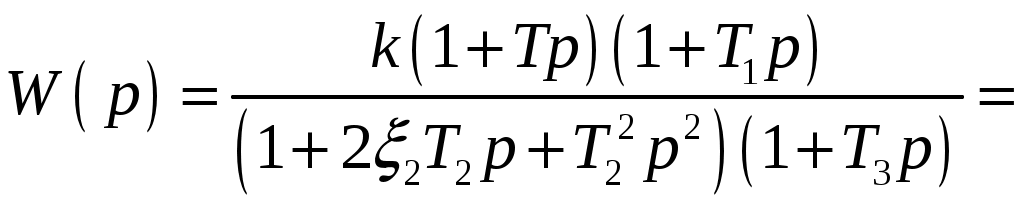
Заданная передаточная функция представляется в виде произведения типовых звеньев [1]: 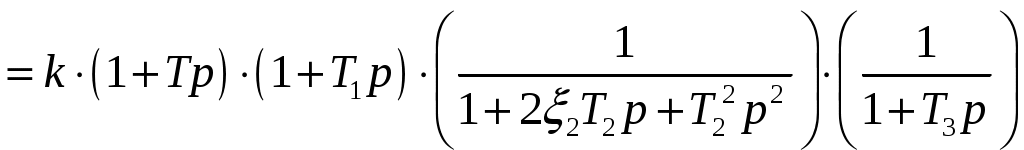.Коэффициент передачи системы в децибелах по формуле и сопрягающие частоты звеньев, входящих в систему по формуле: .Таблица 4 – Коэффициенты и сопрягающие частоты

Коэффициенты и постоянные времени	[раз]	, с	, с	, с	, с
	30	0,2	0,1	0,2	0,2
Сопрягающие частоты	[дБ]	, рад/с	, рад/с	, рад/с	, рад/с
	29,54	5	10	5	5

В системе присутствует два форсирующих, колебательное и апериодическое (инерционное) звенья.Построим АЧХ всех звеньев системы на одном графике [1], затем «сложим координаты» всех графиков в децибелах, чтобы получилась одна кривая (рис. 3). Аналогично поступаем при построении ФЧХ системы (рис. 4).

---

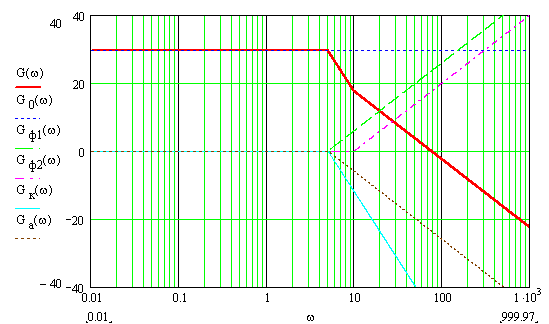
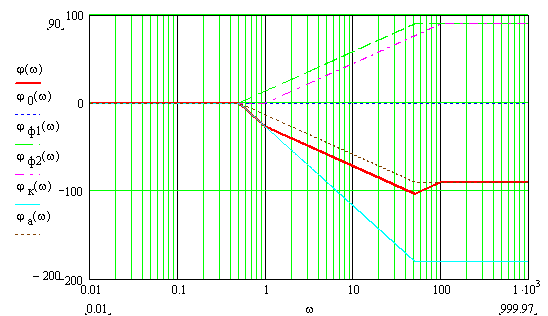
Рисунок 3 – АЧХ системы и типовых звеньевРисунок 4 – ФЧХ системы и типовых звеньевТаким образом, точки перегиба АЧХ находятся на частотах: 5; 10 рад/с, а ФЧХ: 0,5; 1; 50; 100 рад/с.Ответ на второе задание первой контрольной работы запишем в виде:АЧХ: 0 дБ/дек, 5 рад/с, –40 дБ/дек, 10 рад/с, –20 дБ/дек;ФЧХ: 0,5 рад/с, 0°; 1 рад/с, –27°; 50 рад/с, –104°; 100 рад/с, –90°.

Задание 3

Исследовать на устойчивость и определить запасы устойчивости, по заданному в таблице 5 параметру, замкнутой системы управления по заданной передаточной функции разомкнутой системы РА.Таблица 5 – Параметры системы и критерий устойчивости

№						Критерий	Параметр
66	30	0,2	0,1	0,2	0,2	Гурвица

Решение

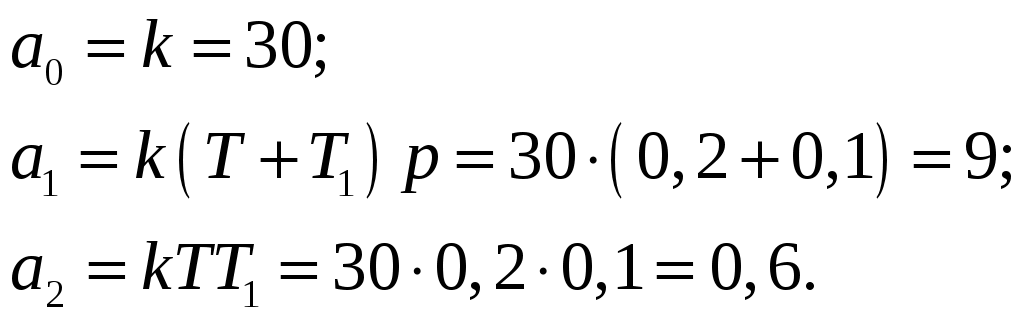
Числитель и знаменатель передаточной функции представим в виде полиномов, для этого раскроем скобки: ;Аналогично для знаменателя: ;

---