ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0 создает магнитный поток Φ, который совпадает с током I0 по фазе. Как уже указывалось, магнитный поток Φ индуктирует в первичной обмотке э.д.с. Е1, а во вторичной обмотке - э.д.с. Е2. Напомним, что всякая э.д.с., индуктируемая синусоидально изменяющимся магнитным потоком, отстает от потока по фазе на 90°. Поэтому векторы E1 и E2 мы откладываем под углом 90° от потока в сторону, обратную вращению векторов. Индуктированную в первичной обмотке э.д.с. Е1 уравновешивает напряжение сети U1.
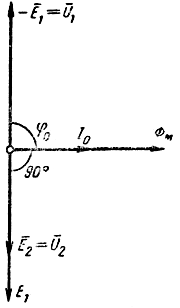
Рис. 2. Векторная диаграмма холостого хода идеального трансформатора
Э.д.с. E1 и напряжение U1 равны и взаимно противоположны (падение напряжения в первичной обмотке при этом режиме очень мало и им можно пренебречь).
Из векторной диаграммы видно, что ток I0, потребляемый идеальным трансформатором при холостой работе, отстает от напряжения сети U1 на 90°, т. е. является чисто реактивным.
У реального трансформатора из-за потерь в стали (на вихревые токи и гистерезис) возникает сдвиг по фазе между током холостого хода I0 и магнитным потоком Φ, причем ток будет опережать магнитный поток. Ток холостого хода I0 трансформатора имеет две составляющие (рис. 3): 1 - активную Ia = I0 ⋅ cos φ0, вызванную потерями в стали (эта составляющая очень мала, так как малы потери холостого хода), 2 - реактивную Ip = I0 ⋅ sin φ0, называемую током намагничивания, создающую магнитный поток Φ и совпадающую с ним по фазе. Так как активная составляющая I0 ⋅ cos φ0 мала, то намагничивающий ток почти равен всему току холостого хода I0. Поэтому I0 является почти целиком реактивным. В режиме холостого хода ток во вторичной обмотке отсутствует и поэтому напряжение на зажимах вторичной обмотки равно э.д.с., индуктированной в этой обмотке:
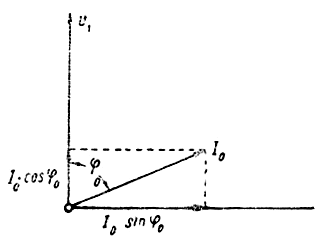
Рис. 3. Диаграмма тока холостого хода
§ 3. НАГРУЗОЧНЫЙ РЕЖИМ ТРАНСФОРМАТОРА
Нагрузочным режимом трансформатора называется режим, при котором вторичная обмотка замкнута на какое-либо сопротивление (рис. 4). При этом во вторичной обмотке будет проходить ток I0, который создает свой магнитный поток Φ2. Таким образом, при нагрузке трансформатора в нем будут действовать намагничивающие силы (сокращенно н. с.) двух обмоток, а в
сердечнике его будет проходить магнитный поток, (полученный действием н. с. обеих обмоток.
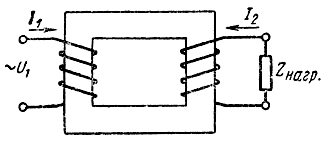
Рис. 4. Нагрузочный режим трансформатора
Согласно правилу Ленца магнитный поток вторичной обмотки стремится уменьшить поток первичной обмотки. Однако результирующий магнитный поток должен остаться постоянным (точнее, почти постоянным). Объясняется это тем, что индуктированная им э.д.с. Е1 при неизменном напряжении сети U1 должна остаться почти неизменной и почти равной напряжению U1, поскольку э.д.с. Е1 все время уравновешивается приложенным напряжением U1, а падение напряжения в обмотке невелико. Построим векторную диаграмму для режима идеального трансформатора в случае, когда к зажимам его вторичной обмотки подключено активное сопротивление Zнагр = rнагр.
Магнитный поток трансформатора Φ и намагничивающий ток I0 совпадают по фазе (рис. 5). Электродвижущие силы Е1 и E21 отстают по фазе на 90° от магнитного потока Φ. Так как нагрузка активная и трансформатор не имеет потерь, то ток I21 совпадает по фазе с э.д.с. E21. При нагрузке трансформатора геометрическая сумма намагничивающих сил первичной и вторичной обмоток будет почти равна намагничивающей силе первичной обмотки при холостом ходе:
I¯1w1 + I¯2w2 ≈ I¯0w1.
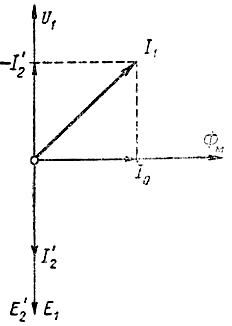
Рис. 5. Векторная диаграмма идеального трансформатора при активной нагрузке
Это вытекает из постоянства результирующего магнитного потока Φ при различных режимах работы трансформатора, если к нему подведено заданное напряжение U1.
Намагничивающая сила вторичной обмотки согласно правилу Ленца будет стремиться уменьшить поток первичной обмотки. Поэтому по виткам первичной обмотки должен проходить такой ток I1, который возбуждал бы по-прежнему магнитный поток Φ и, кроме того, компенсировал размагничивающее действие вторичной обмотки. Иначе говоря, намагничивающая сила первичной обмотки I¯1w1 должна слагаться из намагничивающей силы I¯0w1, создающей поток Φ, и намагничивающей силы - I¯2w2 компенсирующей намагничивающую силу вторичной обмотки I¯
2w2:
I¯1w1 = I¯0w1 - I¯2w2.
Сократив на w1 обе части уравнения, получим
I¯1 = I¯0 - I¯2 w2/w1 = I¯0 + (- I'2),
т.е. первичный ток (I¯1) равен геометрической сумме двух составляющих: одна из них (I¯0) обеспечивает создание основного потока Φ в магнитопроводе, а другая (- I12) компенсирует размагничивающее действие вторичного тока.
Таким образом, любое изменение нагрузочного тока во вторичной цепи трансформатора сопровождается соответствующим изменением тока, потребляемого трансформатором из сети.
До сих пор мы исходили из предположения, что магнитный поток Φ трансформатора целиком замыкается через сердечник. В действительности дело обстоит несколько иначе. Большая часть магнитных потоков, создаваемых первичной и вторичной обмотками трансформатора, замыкается через сердечник, другая - меньшая часть - в виде потоков рассеяния Фp1 и Фр2 замыкается вокруг отдельных витков через воздух (рис. 194). Здесь первичная и вторичная обмотки для наглядности расположены на различных стержнях. В действительности же для уменьшения потоков рассеяния Фр1 и Фр2 обмотки помещают на обоих стержнях.
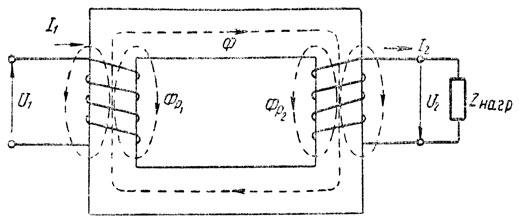
Рис. 194. Магнитные потоки трансформатора
Потоки рассеяния индуктируют в своих обмотках э.д.с., абсолютные величины которых могут быть определены по формулам:
E¯p1 = 2πfLp1I1;
E¯p2 = 2πfLp2I2,
где Lp1 и Lр2 - индуктивности рассеяния обмоток.
Обозначая
x1 = 2πfLp1, x2 = 2πfLp2,
получим;
Е¯р1 = - I¯1x1;
Е¯р2 = - I¯2x2,
где x1 и x2 - индуктивные сопротивления обмоток.
Рассматривая идеальный трансформатор, мы не учитывали падения напряжения в его обмотках, полагая U1 = E1(по абсолютной величине) и U2 = E2. В действительности, падение напряжения в каждой из обмоток составляет около 3% (для силовых трансформаторов, устанавливаемых на промышленных предприятиях), т. е. если бы коэффициент трансформации был равен единице (w1 = w2), то U2 отличалось бы от U1 примерно на 5-6%. Таким образом, напряжение U1, приложенное к зажимам первичной обмотки, должно уравновесить:
э.д.с. E1, индуктированную магнитным потоком трансформатора;
э.д.с. Eр1, индуктированную потоком рассеяния Φр1;
падение напряжения I1r1 в активном сопротивлении r. Следовательно, вектор первичного напряжения U¯1должен быть равен геометрической сумме - Е¯1, - E¯р1 и I¯1r1.
Таким образом, уравнение э.д.с. и напряжений первичной обмотки будет
U¯1 = (- Е¯1) + (- Е¯p1) + I¯1r1 = - Е¯1 + I¯1¯x¯1 + I¯1¯r¯1.
Напряжение U12 на зажимах вторичной обмотки трансформатора во время нагрузочного режима работы отличается от э.д.с. E12 на величину падения напряжения во вторичной обмотке:
U¯12 = E¯12 - I¯'2z'2.
Ток I12, проходя по виткам вторичной обмотки, вызывает активное падение напряжения I12r12, обусловленное наличием активного сопротивления r, и индуктивное падение напряжения I12x12 в индуктивном сопротивлении x12, вызванное потоком рассеяния вторичной обмотки.
Таким образом,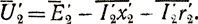
Следовательно, для получения вектора вторичного напряжения U12 необходимо из вектора вторичной э.д.с. E12вычесть векторы падений напряжений: активного - I¯12r¯12 и индуктивного - I¯12x¯12.
Построим векторную диаграмму нагруженного трансформатора в случае активно-индуктивной нагрузки (наиболее часто встречающийся случай). Построение диаграммы начнем с вектора основного магнитного потока Φ (рис. 195). Вектор тока I0 опережает по фазе поток Φ.
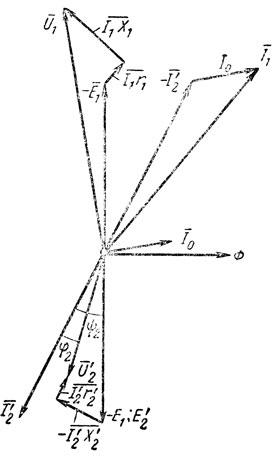
Рис. 195. Векторная диаграмма трансформатора под нагрузкой
Магнитный поток Φ, проходя по сердечнику, индуктирует в первичной обмотке э.д.с. Е1 и во вторичной обмотке э.д.с. E12, которые отстают от потока на 90°. Так как нагрузку трансформатора мы выбрали активно-индуктивной, то ток вторичной обмотки I12 отстает от э.д.с. Е12 на угол Ψ2. Вычитая из вектора E12 векторы активного и индуктивного падений напряжения во вторичной обмотке, получим вектор вторичного напряжения U12.
Для получения вектора тока в первичной обмотке воспользуемся уравнением
I¯1 = I¯0 + (- I¯12).
Откладывая вектор I12 в обратном направлении, получим вектор - I12 и, складывая его с вектором I0, получим вектор I1.
Для получения напряжения U1 первичной обмотки трансформатора применим уравнение, которое мы получили выше, а именно:
U¯1 = -E¯1 + I¯1r1 + I¯1х1.
Отложив вектор - E1 и складывая его с вектором активного и индуктивного падений напряжений в первичной обмотке, получим вектор U1.
Из векторной диаграммы видно, что увеличение нагрузки трансформатора приводит к увеличению тока I12, а это вызывает в свою очередь увеличение тока I1, потребляемого трансформатором из сети.

Рис. 2. Векторная диаграмма холостого хода идеального трансформатора
Э.д.с. E1 и напряжение U1 равны и взаимно противоположны (падение напряжения в первичной обмотке при этом режиме очень мало и им можно пренебречь).
Из векторной диаграммы видно, что ток I0, потребляемый идеальным трансформатором при холостой работе, отстает от напряжения сети U1 на 90°, т. е. является чисто реактивным.
У реального трансформатора из-за потерь в стали (на вихревые токи и гистерезис) возникает сдвиг по фазе между током холостого хода I0 и магнитным потоком Φ, причем ток будет опережать магнитный поток. Ток холостого хода I0 трансформатора имеет две составляющие (рис. 3): 1 - активную Ia = I0 ⋅ cos φ0, вызванную потерями в стали (эта составляющая очень мала, так как малы потери холостого хода), 2 - реактивную Ip = I0 ⋅ sin φ0, называемую током намагничивания, создающую магнитный поток Φ и совпадающую с ним по фазе. Так как активная составляющая I0 ⋅ cos φ0 мала, то намагничивающий ток почти равен всему току холостого хода I0. Поэтому I0 является почти целиком реактивным. В режиме холостого хода ток во вторичной обмотке отсутствует и поэтому напряжение на зажимах вторичной обмотки равно э.д.с., индуктированной в этой обмотке:

Рис. 3. Диаграмма тока холостого хода
§ 3. НАГРУЗОЧНЫЙ РЕЖИМ ТРАНСФОРМАТОРА
Нагрузочным режимом трансформатора называется режим, при котором вторичная обмотка замкнута на какое-либо сопротивление (рис. 4). При этом во вторичной обмотке будет проходить ток I0, который создает свой магнитный поток Φ2. Таким образом, при нагрузке трансформатора в нем будут действовать намагничивающие силы (сокращенно н. с.) двух обмоток, а в
сердечнике его будет проходить магнитный поток, (полученный действием н. с. обеих обмоток.

Рис. 4. Нагрузочный режим трансформатора
Согласно правилу Ленца магнитный поток вторичной обмотки стремится уменьшить поток первичной обмотки. Однако результирующий магнитный поток должен остаться постоянным (точнее, почти постоянным). Объясняется это тем, что индуктированная им э.д.с. Е1 при неизменном напряжении сети U1 должна остаться почти неизменной и почти равной напряжению U1, поскольку э.д.с. Е1 все время уравновешивается приложенным напряжением U1, а падение напряжения в обмотке невелико. Построим векторную диаграмму для режима идеального трансформатора в случае, когда к зажимам его вторичной обмотки подключено активное сопротивление Zнагр = rнагр.
Магнитный поток трансформатора Φ и намагничивающий ток I0 совпадают по фазе (рис. 5). Электродвижущие силы Е1 и E21 отстают по фазе на 90° от магнитного потока Φ. Так как нагрузка активная и трансформатор не имеет потерь, то ток I21 совпадает по фазе с э.д.с. E21. При нагрузке трансформатора геометрическая сумма намагничивающих сил первичной и вторичной обмоток будет почти равна намагничивающей силе первичной обмотки при холостом ходе:
I¯1w1 + I¯2w2 ≈ I¯0w1.

Рис. 5. Векторная диаграмма идеального трансформатора при активной нагрузке
Это вытекает из постоянства результирующего магнитного потока Φ при различных режимах работы трансформатора, если к нему подведено заданное напряжение U1.
Намагничивающая сила вторичной обмотки согласно правилу Ленца будет стремиться уменьшить поток первичной обмотки. Поэтому по виткам первичной обмотки должен проходить такой ток I1, который возбуждал бы по-прежнему магнитный поток Φ и, кроме того, компенсировал размагничивающее действие вторичной обмотки. Иначе говоря, намагничивающая сила первичной обмотки I¯1w1 должна слагаться из намагничивающей силы I¯0w1, создающей поток Φ, и намагничивающей силы - I¯2w2 компенсирующей намагничивающую силу вторичной обмотки I¯
2w2:
I¯1w1 = I¯0w1 - I¯2w2.
Сократив на w1 обе части уравнения, получим
I¯1 = I¯0 - I¯2 w2/w1 = I¯0 + (- I'2),
т.е. первичный ток (I¯1) равен геометрической сумме двух составляющих: одна из них (I¯0) обеспечивает создание основного потока Φ в магнитопроводе, а другая (- I12) компенсирует размагничивающее действие вторичного тока.
Таким образом, любое изменение нагрузочного тока во вторичной цепи трансформатора сопровождается соответствующим изменением тока, потребляемого трансформатором из сети.
До сих пор мы исходили из предположения, что магнитный поток Φ трансформатора целиком замыкается через сердечник. В действительности дело обстоит несколько иначе. Большая часть магнитных потоков, создаваемых первичной и вторичной обмотками трансформатора, замыкается через сердечник, другая - меньшая часть - в виде потоков рассеяния Фp1 и Фр2 замыкается вокруг отдельных витков через воздух (рис. 194). Здесь первичная и вторичная обмотки для наглядности расположены на различных стержнях. В действительности же для уменьшения потоков рассеяния Фр1 и Фр2 обмотки помещают на обоих стержнях.

Рис. 194. Магнитные потоки трансформатора
Потоки рассеяния индуктируют в своих обмотках э.д.с., абсолютные величины которых могут быть определены по формулам:
E¯p1 = 2πfLp1I1;
E¯p2 = 2πfLp2I2,
где Lp1 и Lр2 - индуктивности рассеяния обмоток.
Обозначая
x1 = 2πfLp1, x2 = 2πfLp2,
получим;
Е¯р1 = - I¯1x1;
Е¯р2 = - I¯2x2,
где x1 и x2 - индуктивные сопротивления обмоток.
Рассматривая идеальный трансформатор, мы не учитывали падения напряжения в его обмотках, полагая U1 = E1(по абсолютной величине) и U2 = E2. В действительности, падение напряжения в каждой из обмоток составляет около 3% (для силовых трансформаторов, устанавливаемых на промышленных предприятиях), т. е. если бы коэффициент трансформации был равен единице (w1 = w2), то U2 отличалось бы от U1 примерно на 5-6%. Таким образом, напряжение U1, приложенное к зажимам первичной обмотки, должно уравновесить:
э.д.с. E1, индуктированную магнитным потоком трансформатора;
э.д.с. Eр1, индуктированную потоком рассеяния Φр1;
падение напряжения I1r1 в активном сопротивлении r. Следовательно, вектор первичного напряжения U¯1должен быть равен геометрической сумме - Е¯1, - E¯р1 и I¯1r1.
Таким образом, уравнение э.д.с. и напряжений первичной обмотки будет
U¯1 = (- Е¯1) + (- Е¯p1) + I¯1r1 = - Е¯1 + I¯1¯x¯1 + I¯1¯r¯1.
Напряжение U12 на зажимах вторичной обмотки трансформатора во время нагрузочного режима работы отличается от э.д.с. E12 на величину падения напряжения во вторичной обмотке:
U¯12 = E¯12 - I¯'2z'2.
Ток I12, проходя по виткам вторичной обмотки, вызывает активное падение напряжения I12r12, обусловленное наличием активного сопротивления r, и индуктивное падение напряжения I12x12 в индуктивном сопротивлении x12, вызванное потоком рассеяния вторичной обмотки.
Таким образом,
Следовательно, для получения вектора вторичного напряжения U12 необходимо из вектора вторичной э.д.с. E12вычесть векторы падений напряжений: активного - I¯12r¯12 и индуктивного - I¯12x¯12.
Построим векторную диаграмму нагруженного трансформатора в случае активно-индуктивной нагрузки (наиболее часто встречающийся случай). Построение диаграммы начнем с вектора основного магнитного потока Φ (рис. 195). Вектор тока I0 опережает по фазе поток Φ.

Рис. 195. Векторная диаграмма трансформатора под нагрузкой
Магнитный поток Φ, проходя по сердечнику, индуктирует в первичной обмотке э.д.с. Е1 и во вторичной обмотке э.д.с. E12, которые отстают от потока на 90°. Так как нагрузку трансформатора мы выбрали активно-индуктивной, то ток вторичной обмотки I12 отстает от э.д.с. Е12 на угол Ψ2. Вычитая из вектора E12 векторы активного и индуктивного падений напряжения во вторичной обмотке, получим вектор вторичного напряжения U12.
Для получения вектора тока в первичной обмотке воспользуемся уравнением
I¯1 = I¯0 + (- I¯12).
Откладывая вектор I12 в обратном направлении, получим вектор - I12 и, складывая его с вектором I0, получим вектор I1.
Для получения напряжения U1 первичной обмотки трансформатора применим уравнение, которое мы получили выше, а именно:
U¯1 = -E¯1 + I¯1r1 + I¯1х1.
Отложив вектор - E1 и складывая его с вектором активного и индуктивного падений напряжений в первичной обмотке, получим вектор U1.
Из векторной диаграммы видно, что увеличение нагрузки трансформатора приводит к увеличению тока I12, а это вызывает в свою очередь увеличение тока I1, потребляемого трансформатором из сети.