Лабораторная работа №4

Определение вязкости жидкости методом Стокса

Вязкость – появление сил трения между слоями газа или жидкости, движущимися относительно друг друга параллельно с различными по величине скоростями. Вследствие обмена молекулами за счет их хаотического теплового движения более быстрый слой ускоряет соседний с ним медленный слой, и, наоборот. Силы внутреннего трения направлены по касательным к слоям газа или жидкости.

Скорость беспорядочного теплового движения молекул в текущем газе или жидкости в среднем одинакова во всех точках рассматриваемого пространства, но скорость направленного движения одинакова только для молекул данного слоя газа или жидкости и различна для различных слоев. В жидкости внутреннее трение в значительной мере определяется действием межмолекулярных сил. Расстояние между молекулами в жидкости невелики, а сила взаимодействия значительны. Молекулы жидкости колеблются около положений равновесия.

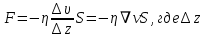– расстояние между двумя ближайшими слоями жидкости, S – площадь между этими слоями, 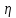– динамический коэффициент внутреннего трения или просто коэффициент вязкости.

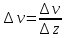– поперечный градиент скорости, показывающий как изменяется скорость потока в направлении оси Z.

Стокс установил, что при небольших скоростях движения, то есть при малых значениях числа Рейнольдса, сила сопротивления, с которой действует жидкая среда на движущееся твердое тело, пропорциональна коэффициенту динамической вязкости жидкости, скорости движения тела относительно жидкости и характерному размеру тел. Для шара, если в качестве взять радиус шара, коэффициент пропорциональности равен 6П

---

Сила сопротивления движения шарика в жидкостях при небольших скоростях в соответствии с формулой Стокса равна (для малых размеров и малых скоростей движения относительно жидкости):

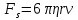
Закон Стокса применим, если течение жидкости ламинарное, такое, при котором каждый выделенный слой скользит параллельно соседним, не перемешиваясь с ним.

Турбулентное или вихревое – течение, при возрастании скорости в жидкости которого, возникает интенсивное перемешивание и вихреобразование. В этом случае сила сопротивления становится пропорциональной квадрату скорости.

Характер течения жидкости определяется безразмерным числом Рейнольдса:

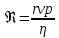, где r – величина, характеризующая линейные размеры тела, обтекаемого жидкостью, v – скорость течения, p – плотность жидкости

Если Re превышает определенное критическое значение, то поток становится турбулентным; при значениях меньше критического – ламинарным. Число Рейнольдса можно использовать в качестве критерия применимости закона Стокса.

Контрольные вопросы
1. Силы внутреннего трения и их природа. От каких факторов зависит коэффициент динамической вязкости?
Вязкость – появление сил трения между слоями газа или жидкости, движущимися относительно друг друга параллельно с различными по величине скоростями. Вследствие обмена молекулами за счет их хаотического теплового движения более быстрый слой ускоряет соседний с ним медленный слой, и, наоборот. Силы внутреннего трения направлены по касательным к слоям газа или жидкости.

– динамический коэффициент внутреннего трения или просто коэффициент вязкости. Зависит от свойств жидкости и температуры.
2. Напишите формулу Ньютона для сил внутреннего трения. Поясните понятие градиента скорости течения жидкости с помощью рисунка.
– расстояние между двумя ближайшими слоями жидкости, S – площадь между этими слоями, – динамический коэффициент внутреннего трения или просто коэффициент вязкости.

---

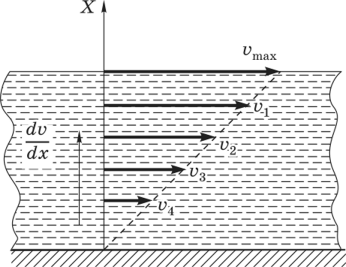
3. Объясните метод Стокса определения вязкости жидкости и дайте вывод формулы 9.
Стокс установил, что при небольших скоростях движения, то есть при малых значениях числа Рейнольдса, сила сопротивления, с которой действует жидкая среда на движущееся твердое тело, пропорциональна коэффициенту динамической вязкости жидкости, скорости движения тела относительно жидкости и характерному размеру тел. Для шара, если в качестве взять радиус шара, коэффициент пропорциональности равен 6П

Сила сопротивления движения шарика в жидкостях при небольших скоростях в соответствии с формулой Стокса равна (для малых размеров и малых скоростей движения относительно жидкости):

Закон Стокса применим, если течение жидкости ламинарное

4. Как различаются течения ламинарное и турбулентное. Число Рейнольдса.
Течение жидкости ламинарное, такое, при котором каждый выделенный слой скользит параллельно соседним, не перемешиваясь с ним.

Турбулентное или вихревое – течение, при возрастании скорости в жидкости которого, возникает интенсивное перемешивание и вихреобразование. В этом случае сила сопротивления становится пропорциональной квадрату скорости.

Характер течения жидкости определяется безразмерным числом Рейнольдса:

, где r – величина, характеризующая линейные размеры тела, обтекаемого жидкостью, v – скорость течения, p – плотность жидкости

Если Re превышает определенное критическое значение, то поток становится турбулентным; при значениях меньше критического – ламинарным. Число Рейнольдса можно использовать в качестве критерия применимости закона Стокса.
5. Получите формулы 14-16

---

Смотрите также файлы

• На странице создания приложения указать тип "Вебприложение".docx

• Год написания 1866 г. История создания.docx

• Колледж Инфраструктурных Технологий.docx

• Кыргызская философия.pdf

• 2. в этом городе Печориным раскрыта банда контрабандистов.docx