Файл: Решение. Разобьем множество всех возможных выборок, удовлетворяющих заданному условию, на два непересекающихся подмножества.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1. Сколькими способами из колоды в 36 карт можно выбрать неупорядоченный набор из 4-х карт так, чтобы в этом наборе было бы в точности 2 карты красной масти, 2 туза?
Решение.
Разобьем множество всех возможных выборок, удовлетворяющих заданному условию, на два непересекающихся подмножества.
| Среди четырех выбранных карт | |
| 2 туза черной масти и 2 карты красной масти | 2 туза красной масти и 2 карты черной масти |
| Количество способов выбрать: | |
|
|
| Число выборок заданной структуры равно: | |
| 1* 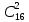 = 1*120 = 120. = 1*120 = 120. | 1* 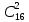 = 1*120 = 120. = 1*120 = 120. |
Общее число способов выбора 4-х карт, удовлетворяющих условию задачи, составляет:
120+120 = 240.
Задание 2. Дано множество А = {0, 3, 8, 9}.
Для каждого пункта, указанного ниже, нужно найти количество объектов, а также получить сами соответствующие объекты.
-
Сколькими способами из множества А можно выбрать 2 различные цифры? -
Сколько различных трехзначных чисел можно записать из цифр, входящих в множество А (цифры в записи числа могут повторяться)? -
Сколько различных трехзначных чётных (нечётных) чисел можно записать из цифр, входящих в множество А (цифры в записи числа могут повторяться)? -
Сколько различных трехзначных чисел можно записать из цифр, входящих в множество А (все цифры в записи числа различны)? -
Сколько различных трехзначных чётных (нечётных) чисел можно записать из цифр, входящих в множество А (все цифры в записи числа различны)?
Решение.
Дано множество А = {0, 3, 8, 9}.
-
Сколькими способами из множества А можно выбрать 2 различные цифры?
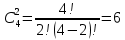 .
.Получим сами сочетания:
{{0,9}, {0,8}, {0,3}, {3,9}, {3,8}, {8,9}}.
-
Сколько различных трехзначных чисел можно записать из цифр, входящих в множество А (цифры в записи числа могут повторяться)?
3*4*4=48.
Получим эти числа в виде векторов (кортежей):
(A\{0}) A×A = {3, 8, 9} × {0, 3, 8, 9} × {0, 3, 8, 9} =
= {(3,0,0), (3,0,3), (3,0,8), (3,0,9), (3,3,0), (3,3,3), (3,3,8), (3,3,9), (3,8,0), (3,8,3), (3,8,8), (3,8,9), (3,9,0), (3,9,3), (3,9,8), (3,9,9), (8,0,0), (8,0,3), (8,0,8), (8,0,9), (8,3,0), (8,3,3), (8,3,8), (8,3,9), (8,8,0), (8,8,3), (8,8,8), (8,8,9), (8,9,0), (8,9,3), (8,9,8), (8,9,9), (9,0,0), (9,0,3), (9,0,8), (9,0,9), (9,3,0), (9,3,3), (9,3,8), (9,3,9), (9,8,0), (9,8,3), (9,8,8), (9,8,9), (9,9,0), (9,9,3), (9,9,8), (9,9,9)}.
Полученных кортежей, соответствующих заданным трехзначным числам, действительно 48.
-
Сколько различных трехзначных нечетных чисел можно записать из цифр, входящих в множество А (цифры в записи числа могут повторяться)?
Здесь последняя цифра выбирается из подмножества {3,9} множества A. Имеем:
3*4*2= 24.
Получим соответствующие числа.
(A\{0}) ×A× {3, 9} = {3, 8, 9} × {0, 3, 8, 9} × {3, 9} =
={(3,0,3), (3,0,9), (3,3,3), (3,3,9), (3,8,3), (3,8,9), (3,9,3), (3,9,9), (8,0,3), (8,0,9), (8,3,3), (8,3,9), (8,8,3), (8,8,9), (8,9,3), (8,9,9), (9,0,3), (9,0,9), (9,3,3), (9,3,9), (9,8,3), (9,8,9), (9,9,3), (9,9,9).
Сколько различных трехзначных четных чисел можно записать из цифр, входящих в множество А (цифры в записи числа могут повторяться)?
Здесь последняя цифра выбирается из подмножества {0, 2} множества A. Имеем:
3*4*2=24.
Получим соответствующие числа.
(A\{0}) ×A× {3, 9} = {3, 8, 9} × {0, 3, 8, 9} × {0, 8} =
={(3,0,0), (3,0,8), (3,3,0), (3,3,8), (3,8,0), (3,8,8), (3,9,0), (3,9,8), (8,0,0), (8,0,8), (8,3,0), (8,3,8), (8,8,0), (8,8,8), (8,9,0), (8,9,8), (9,0,0), (9,0,8), (9,3,0), (9,3,8), (9,8,0), (9,8,8), (9,9,0), (9,9,8).
-
Сколько различных трехзначных чисел можно записать из цифр, входящих в множество А (все цифры в числе различны)?
Первая цифра числа выбирается из множества A\{0} (3 варианта). После выбора первой цифры один из элементов множества A\{0} уже использован и не может быть повторно выбран, но зато элемент 0 возвращается в рассмотрение – его можно использовать в качестве второй цифры. Таким образом, для выбора второй цифры также есть 3 возможности. К моменту выбора третьей цифры, две цифры из имеющихся четырёх уже выбраны. Поэтому остается 2 возможности выбрать третью цифру. Имеем:
3*3*2=18.
Получим эти 18 чисел в виде кортежей.
{3} × ({0}×{8, 9} ∪ {8}×{0, 9} ∪ {9}×{0, 8}) ∪
∪{8} × ({0}×{3, 9} ∪ {3}×{0, 9} ∪ {9}×{0, 3}) ∪
∪ {9} × ({0}×{3, 8} ∪ {3}×{0, 8} ∪ {8}×{0, 3}) =
= {3}×{0}×{8, 9} ∪ {3}×{8}×{0, 9} ∪ {3}×{9}×{0, 8} ∪
∪ {8}×{0}×{3, 9} ∪ {8}×{3}×{0,9} ∪ {8}×{9}×{0, 3} ∪
∪ {9}×{0}×{3, 8} ∪ {9}×{3}×{0, 8} ∪ {9}×{8}×{0, 3} =
= {(3,0,8), (3,0,9), (3,8,0), (3,8,9), (3,9,0), (3,9,8)} ∪
∪ {(8,0,3), (8,0,9), (8,3,0), (8,3,9), (8,9,0), (8,9,3)} ∪
∪ {(9,0,3), (9,0,8), (9,3,0), (9,3,8), (9,8,0), (9,8,3)} =
= {(3,0,8), (3,0,9), (3,8,0), (3,8,9), (3,9,0), (3,9,8), (8,0,3), (8,0,9), (8,3,0), (8,3,9), (8,9,0), (8,9,3), (9,0,3), (9,0,8), (9,3,0), (9,3,8), (9,8,0), (9,8,3)}.
-
Сколько различных трехзначных нечётных чисел можно записать из цифр, входящих в множество А (все цифры в числе различны)?
Последнюю цифру можно выбрать двумя способами из множества {3, 9}. Для выбора первой цифры остается множество {8} и один (не выбранный) элемент множества {3, 9} (т.е. всего две возможности). К моменту выбора третьей цифры остается два невыбранных элемента множества А, т.е. тоже две возможности. Имеем:
2*2*2=8.
Формируем выражение, позволяющее получить искомые числа, в виде кортежей:
Числа вида 3_9: {3} × {0, 8} × {9}
Числа вида 8_3 и 8_9: {8} × ({0} × {3, 9} ∪ {3} × {9} ∪ {9} × {3})
Числа вида 9_3: {9} × {0, 8} × {3}
{3} × {0, 8} × {9}∪{{8} × ({0} × {3, 9} ∪ {3} × {9} ∪ {9} × {3}) ∪{{9} × {0, 8} × {3} =
= {(3, 0, 9), (3, 8, 9), (8, 0, 3), (8, 0, 9), (8, 3, 9), (8, 9, 3), (9, 0, 3), (9, 8, 3)}.
Сколько различных трехзначных чётных чисел можно записать из цифр, входящих в множество А (все цифры в числе различны)?
Последнюю цифру можно выбрать двумя способами – из множества {0,8}. Разобьем множество всех чисел, удовлетворяющих заданным условиям, на два непересекающихся подмножества: в первое подмножество входят все числа, заканчивающиеся на 8 (вида __8),
а во второе – все числа, заканчивающиеся на 0 (вида __ 0).
Для чисел из первого подмножества первую цифру можно выбрать двумя способами (из множества {3, 9}), тогда вторую – тоже двумя способами (0 и одна из оставшихся цифр: 3 или 9). Таким образом, количество чисел в первом подмножестве равно 2*2*1 = 4.
Для чисел из второго подмножества первую цифру можно выбрать тремя способами (из множества {3, 8, 9}), а вторую – двумя способами (из двух элементов множества {3, 8, 9}, которые остались после выбора первой цифры). Таким образом, количество чисел во втором подмножестве равно 3*2*1 = 6.
По правилу суммы получаем общее количество возможных чисел: 4 + 6 = 10, и сами числа:
({3} × {0, 9} ∪ {9} ×{0, 3}) × {8} ∪ ({3} × {8, 9} ∪ {8} × {3, 9} ∪ {9} × ×{3, 8}) × {0} =
= {(3, 0, 8), (3, 9, 8), (9, 0, 8), (9, 3, 8), (3, 8, 0), (3, 9, 0), (8, 3, 0), (8, 9, 0), (9, 3, 0), (9, 8, 0)}.
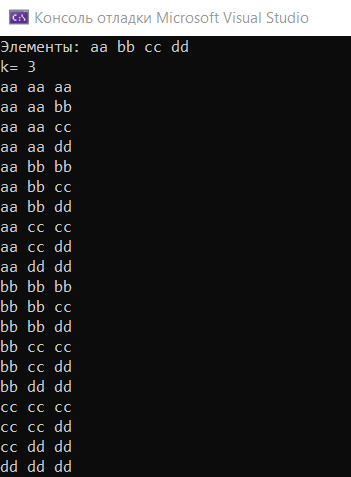
Задание 3. Написать программу для получения из заданных элементов
всех сочетаний заданной длины k с повторениями элементов.
Листинг кода:
#include
using namespace std;
bool next_comb(int index[], const int& n, const int& m)
{
int j = m - 1;
while (index[j] == n && j >= 0)
j--;
if (j < 0)
return false;
if (index[j] >= n)
j--;
index[j]++;
if (j == m - 1)
return true;
for (int k = j + 1; k < m; k++)
index[k] = index[j];
return true;
}
int main()
{
setlocale(LC_ALL, "rus");
string char_set[] = { "aa", "bb", "cc", "dd"};
int N = sizeof(char_set) / sizeof(char_set[0]);
for (int i = 0; i < N; ++i)
std::cout << char_set[i] << " ";
std::cout << std::endl;
int n;
cin >> n;
int k = N > n ? N : n;
int* index = new int[k];
for (int i = 0; i < k; i++)
index[i] = 1;
do
{
for (int i = 0; i < n; ++i)
std::cout << char_set[index[i] - 1] << " ";
std::cout << std::endl;
} while (next_comb(index, N, n));
delete[] index;
//std::cin.get();
}
Пример работы программы: