ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, просто разные методы и итоговые значения будут одинаковыми, только знаки противоположными.
Не могу с уверенностью сказать почему у строителей изгибающий момент направлен в сторону растянутых волокон. Возможно из-за того, что при данном рассмотрении эпюра моментов во многих случаях повторяет изгиб балки.
Мы будем рассматривать метод, которым пользуются строители.
Определяем напряжения M на участке AC
Рассмотрим участок от точки A до точки C.
Значение изгибающего момента в точке A равно нулю, в точке B тоже равно нулю т.к. мы имеем однопролетную шарнирно-опертую балку.
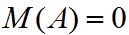
На значение изгибающего момента в точке C влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки C), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до C в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2)
Вычислим значения изгибающего момента в точке C:
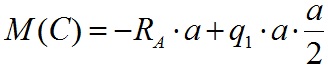
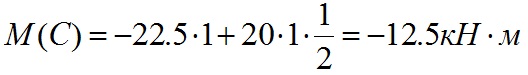
Т.к. на данном участке действует равномерно-распределенная нагрузка, то форма эпюры M на данном участке имеет изгиб в сторону действия нагрузки. Эпюра M на данном участке будет выглядеть следующим образом:
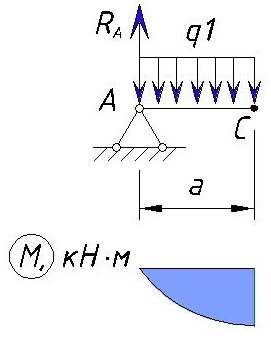
Определяем напряжения M на участке CD
На участке между точками C и D нет никаких нагрузок, а в точке D приложен изгибающий момент M1, поэтому необходимо считать вначале значение изгибающего момента без учета M1 (точка D слева), затем считать с учетом изгибающего момента M1 (точка D справа). На эпюре в точке D будет скачок напряжения изгибающих моментов.
На значение изгибающего момента в точке D влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки D), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до D в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
Вычислим значение изгибающего момента в точке D слева:
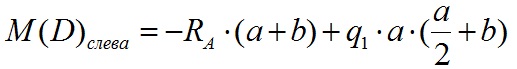
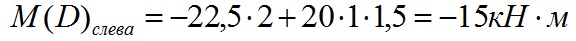
Вычислим значение изгибающего момента в точке D справа:
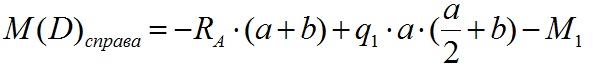
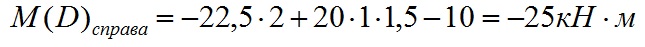
Эпюра M между точками C и D изменяется прямолинейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:
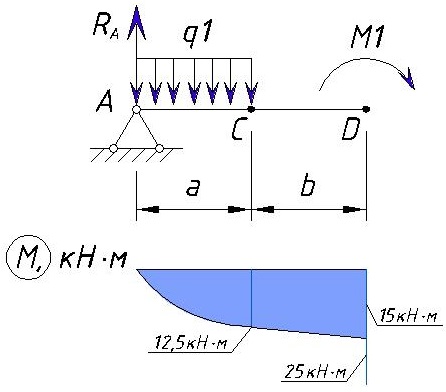
Определяем напряжения M на участке DE
На участке между точками D и E нет никаких нагрузок, а в точке E приложена сосредоточенная нагрузка F1, но т.к. плечо в данной точке равно нулю, то и изгибающий момент сила F не создает в точке E.
На значение изгибающего момента в точке E влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки E), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до E в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b+c)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
Вычислим значение изгибающего момента в точке E:
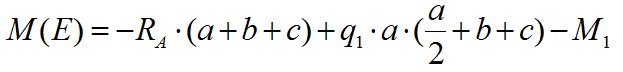
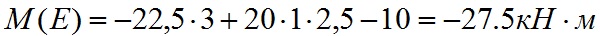
Эпюра M между точками D и E изменяется линейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:
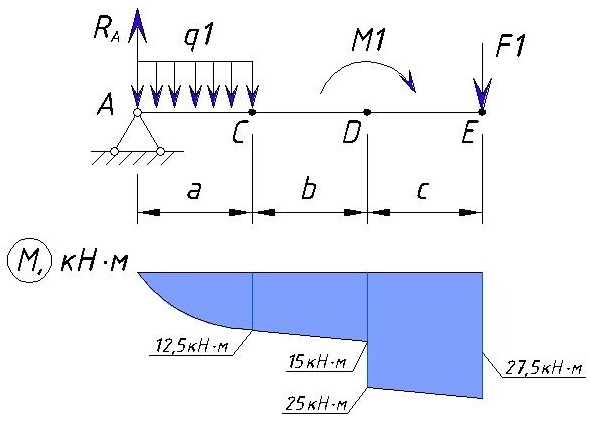
Определяем напряжения M на участке EB
На участке между точками E и B нет никаких нагрузок, а в точке B приложена опорная нагрузка Rb, но т.к. плечо в данной точке равно нулю, то и изгибающий момент опорная сила Rb не создает.
Изгибающий момент в точке B должен быть равен нулю, мы это сейчас проверим.
На значение изгибающего момента в точке B влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки E), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до B в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b+c+d)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
4) Сила F1. Действие силы растягивает верхние волокна, поэтому учитывается со знаком плюс. Плечо действия силы равно d.
Вычислим значение изгибающего момента в точке B:
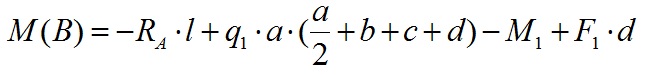
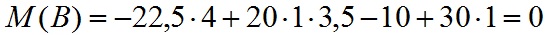
В принципе это тоже самое уравнение, которое мы решали при определении опорных реакций.
Т.к. на участке EB нет никаких нагрузок, то изменение изгибающего момента происходит прямолинейно.
Итоговая эпюра M
Теперь нарисуем всю эпюру M для данного примера
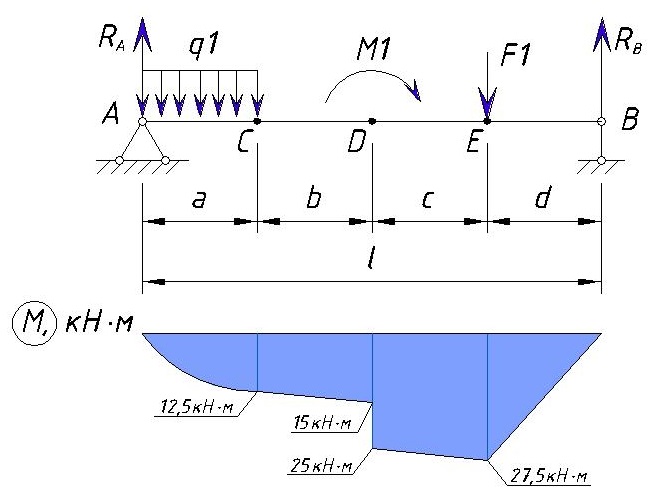
Можно отметить следующие правила при построении эпюры изгибающих моментов:
1) на участке приложения равномерно-распределенной или переменной нагрузки эпюра имеет изгиб
2) на участках где не приложены силы эпюра изменяется прямолинейно
3) в точке где приложен изгибающий момент происходит скачок напряжения
Итоговая эпюра Q и M
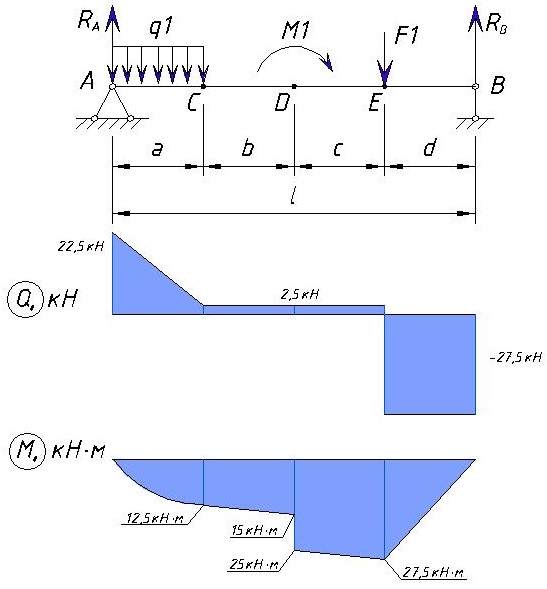
ГАОУ ВПО «Дагестанский государственный университет народного хозяйства»
Реферат
На тему:
«Геометрические правила построения эпюр поперечной силы и изгибающего момента однопролётной балки»
Выполнил:
Студент 2 курса
Группы 9С-22 ИК
Алиханов Ш.К.
Махачкала 2023
Не могу с уверенностью сказать почему у строителей изгибающий момент направлен в сторону растянутых волокон. Возможно из-за того, что при данном рассмотрении эпюра моментов во многих случаях повторяет изгиб балки.
Мы будем рассматривать метод, которым пользуются строители.
Определяем напряжения M на участке AC
Рассмотрим участок от точки A до точки C.
Значение изгибающего момента в точке A равно нулю, в точке B тоже равно нулю т.к. мы имеем однопролетную шарнирно-опертую балку.
На значение изгибающего момента в точке C влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки C), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до C в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2)
Вычислим значения изгибающего момента в точке C:
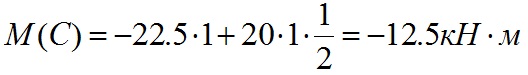
Т.к. на данном участке действует равномерно-распределенная нагрузка, то форма эпюры M на данном участке имеет изгиб в сторону действия нагрузки. Эпюра M на данном участке будет выглядеть следующим образом:

Определяем напряжения M на участке CD
На участке между точками C и D нет никаких нагрузок, а в точке D приложен изгибающий момент M1, поэтому необходимо считать вначале значение изгибающего момента без учета M1 (точка D слева), затем считать с учетом изгибающего момента M1 (точка D справа). На эпюре в точке D будет скачок напряжения изгибающих моментов.
На значение изгибающего момента в точке D влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки D), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до D в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
Вычислим значение изгибающего момента в точке D слева:
Вычислим значение изгибающего момента в точке D справа:
Эпюра M между точками C и D изменяется прямолинейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:

Определяем напряжения M на участке DE
На участке между точками D и E нет никаких нагрузок, а в точке E приложена сосредоточенная нагрузка F1, но т.к. плечо в данной точке равно нулю, то и изгибающий момент сила F не создает в точке E.
На значение изгибающего момента в точке E влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки E), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до E в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b+c)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
Вычислим значение изгибающего момента в точке E:
Эпюра M между точками D и E изменяется линейно т.к. между этими нет сил. Эпюра на этом участке выглядит следующим образом:

Определяем напряжения M на участке EB
На участке между точками E и B нет никаких нагрузок, а в точке B приложена опорная нагрузка Rb, но т.к. плечо в данной точке равно нулю, то и изгибающий момент опорная сила Rb не создает.
Изгибающий момент в точке B должен быть равен нулю, мы это сейчас проверим.
На значение изгибающего момента в точке B влияют следующие силы:
1) Опорная реакция Ra. Действие силы растягивает нижние волокна (если рассматривать силу Ra вокруг точки E), поэтому значение изгибающего момента учитывается со знаком минус. Значение изгибающего момента от действия силы Ra равно произведению этой силы на плечо (расстояние от A до B в данном случае)
2) Равномерно-распределенная нагрузка q1. Действие силы растягивает верхние волокна, поэтому значение изгибающего момента от действия нагрузки q1 принимается со знаком плюс. Значение изгибающего момента от действия равномерно-распределенной нагрузки q1 равно произведению значения этой нагрузки (q1*a) на плечо (расстояние от центра равномерно-распределенной нагрузки до заданной точки, в данном случае a/2+b+c+d)
3) Изгибающий момент M1. Значение изгибающего момента не зависит от расстояния до нагрузки. Для расчета необходимо вначале рассчитать значение слева от точки где приложен данный момент, не учитывая его, и справа с учетом действия этого момента. Т.к. изгибающий момент растягивает нижние волокна, то учитываем его со знаком минус.
4) Сила F1. Действие силы растягивает верхние волокна, поэтому учитывается со знаком плюс. Плечо действия силы равно d.
Вычислим значение изгибающего момента в точке B:
В принципе это тоже самое уравнение, которое мы решали при определении опорных реакций.
Т.к. на участке EB нет никаких нагрузок, то изменение изгибающего момента происходит прямолинейно.
Итоговая эпюра M
Теперь нарисуем всю эпюру M для данного примера

Можно отметить следующие правила при построении эпюры изгибающих моментов:
1) на участке приложения равномерно-распределенной или переменной нагрузки эпюра имеет изгиб
2) на участках где не приложены силы эпюра изменяется прямолинейно
3) в точке где приложен изгибающий момент происходит скачок напряжения
Итоговая эпюра Q и M

ГАОУ ВПО «Дагестанский государственный университет народного хозяйства»
Реферат
На тему:
«Геометрические правила построения эпюр поперечной силы и изгибающего момента однопролётной балки»
Выполнил:
Студент 2 курса
Группы 9С-22 ИК
Алиханов Ш.К.
Махачкала 2023