С учетом ОДЗ получаем решение неравенства:

Ответ:

Из рассмотренного метода рационализации вытекают следствия:



Пример. Решите неравенство:

Решение.

ОДЗ:











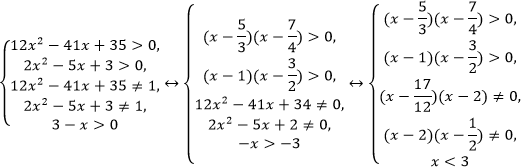
Применим метод рационализации:





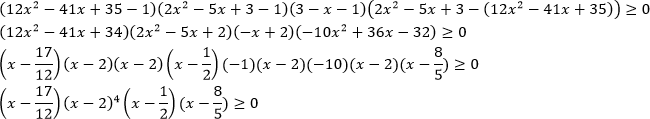
С учетом ОДЗ:

Ответ:

Метод рационализации для неравенств с модулем



При сравнении двух чисел по модулю нас не интересует знак числа, поэтому можем от знака избавиться при помощи чётной степени. избавит нас от знака. При дальнейшей работе с полученным неравенством выполнять возведение в квадрат не обязательно, лучше применить формулу разности квадратов.

Пример. Решите неравенство

---

Решение. Воспользуемся методом рационализации:





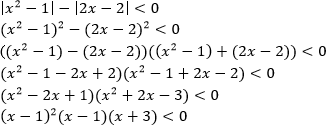
Решением неравенства является интервал (-3;1)

Ответ:

Пример. Решите неравенство



Решение. Воспользуемся равносильным переходом:





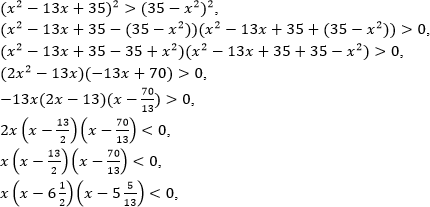
Решением неравенства является промежуток

Ответ:

Метод рационализации для иррациональных неравенств



Пример. Решите неравенство .

Решение.

ОДЗ (находим ОДЗ для меньшего из выражений, ОДЗ для большего выражения выполнится автоматически):



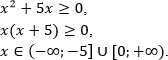
Воспользуемся методом рационализации:



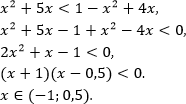
С учетом ОДЗ получаем окончательное решение неравенства:

Ответ:

Метод рационализации для показательных неравенств

---

Для показательно-степенных неравенств действуют те же правила, что и для логарифма. При основании, большем 1, знак неравенства мы можем сохранить, при основании меньше единицы, знак неравенства должен измениться при переходе к степеням. Тогда мы можем записать это, как произведение двух скобок, в первой мы будем сравнивать основание с единицей, а во второй – значения показателей степеней.

Пример. Решите неравенство



ОДЗ:

Воспользуемся методом рационализации:





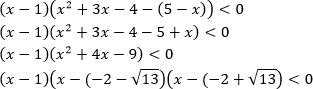
Видим, что решением является промежуток:

С учетом ОДЗ:

Ответ:

Сведем все рассмотренные равносильные преобразования в таблицу

---

Смотрите также файлы

• Практическая работа к теме Семья традиции.docx

• Решение экрана, тип локомотива и нажать кнопку Запуск тренажёра.rtf

• Планирование потребностей в материальных ресурсах и персонале службы.docx

• Методические указания студенту по выполнению программы преддипломной практики.docx

• Сущность и функции управления производством на режимных объектах.docx