Файл: Сабаты таырыбы Бір фазалы синусоидалы ток тізбектері.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Бір фазалы синусоидалы ток тізбектерітақырыбы бойынша сабақта да практикалық жұмысты (шығармашылық сипаттағы тапсырмалар) орындатамыз
Сабақтың тақырыбы: Бір фазалы синусоидалы ток тізбектері.
Сабақтың мақсаты: Бір фазалы, екі фазалы және үш фазалы токтар, айнымалы токты алу әдістері және оны сипаттайтын шамаларды күрделі схемаларға қолдану
Тақырып бойынша бір фазалы синусоидалы ток тізбегін есептеу мысалын қарастырамыз.
28-суреттегі схемада ЭҚК шамалары және кедергі, конденсатор, катушка параметрлері берілген. Осы тізбектегі токтарды табыңыз?
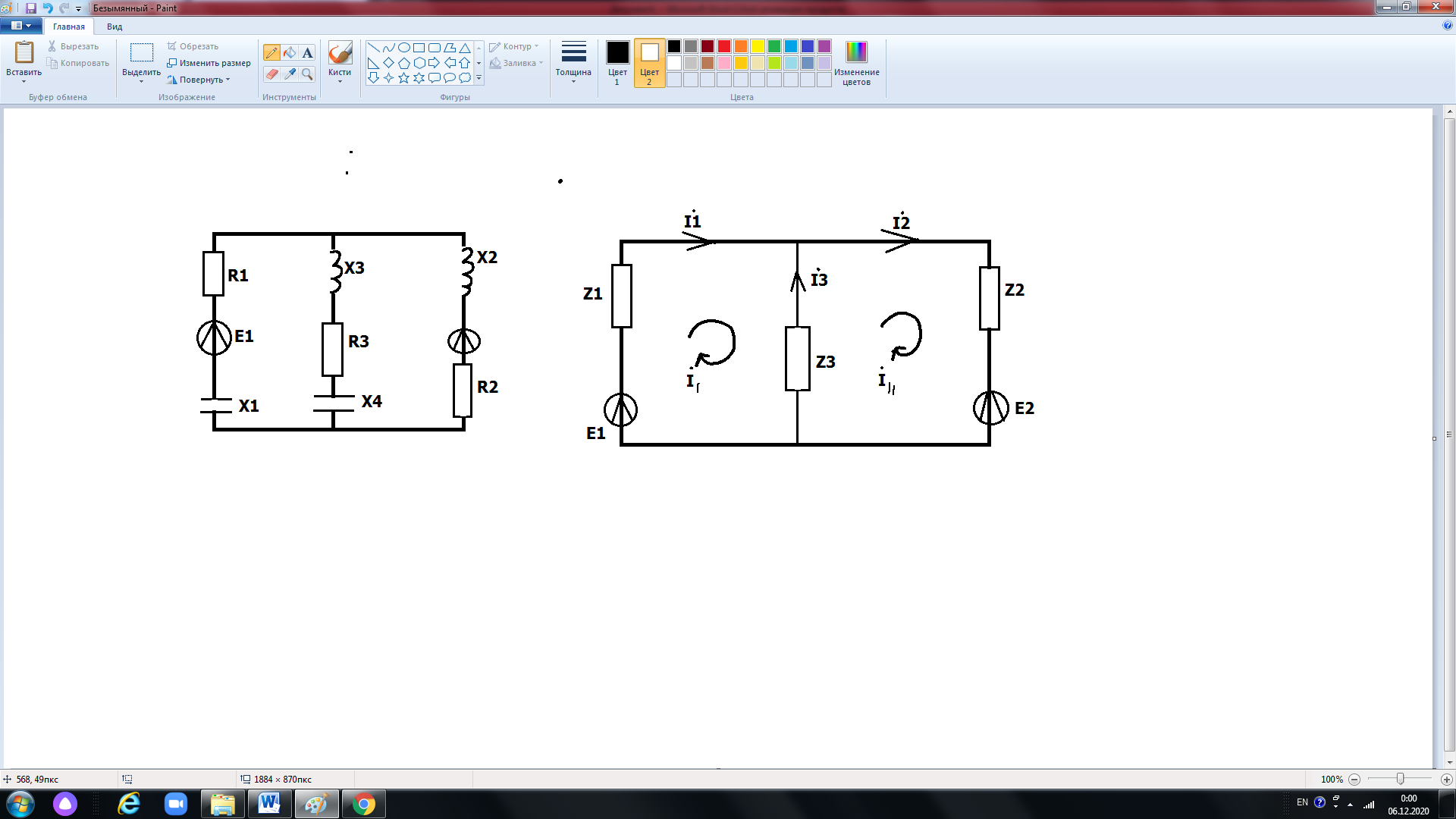
Сурет 28 –Тармақталған айнымалы токтың электр тізбегі
Есептің шығарылу жолы:
Контурлы токтар әдісімен тармақтардағы токтарды есептеу
ЭҚК мен тармақтардың кедергісін комплексті түрде жазамыз:
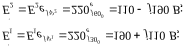
Мұнда
, ЭҚК мәні.Комплексті кедергілер:
Ом;
Ом;
Ом.Эквивалентті есептеу сұлбасы 29 – суретте көрсетілген.
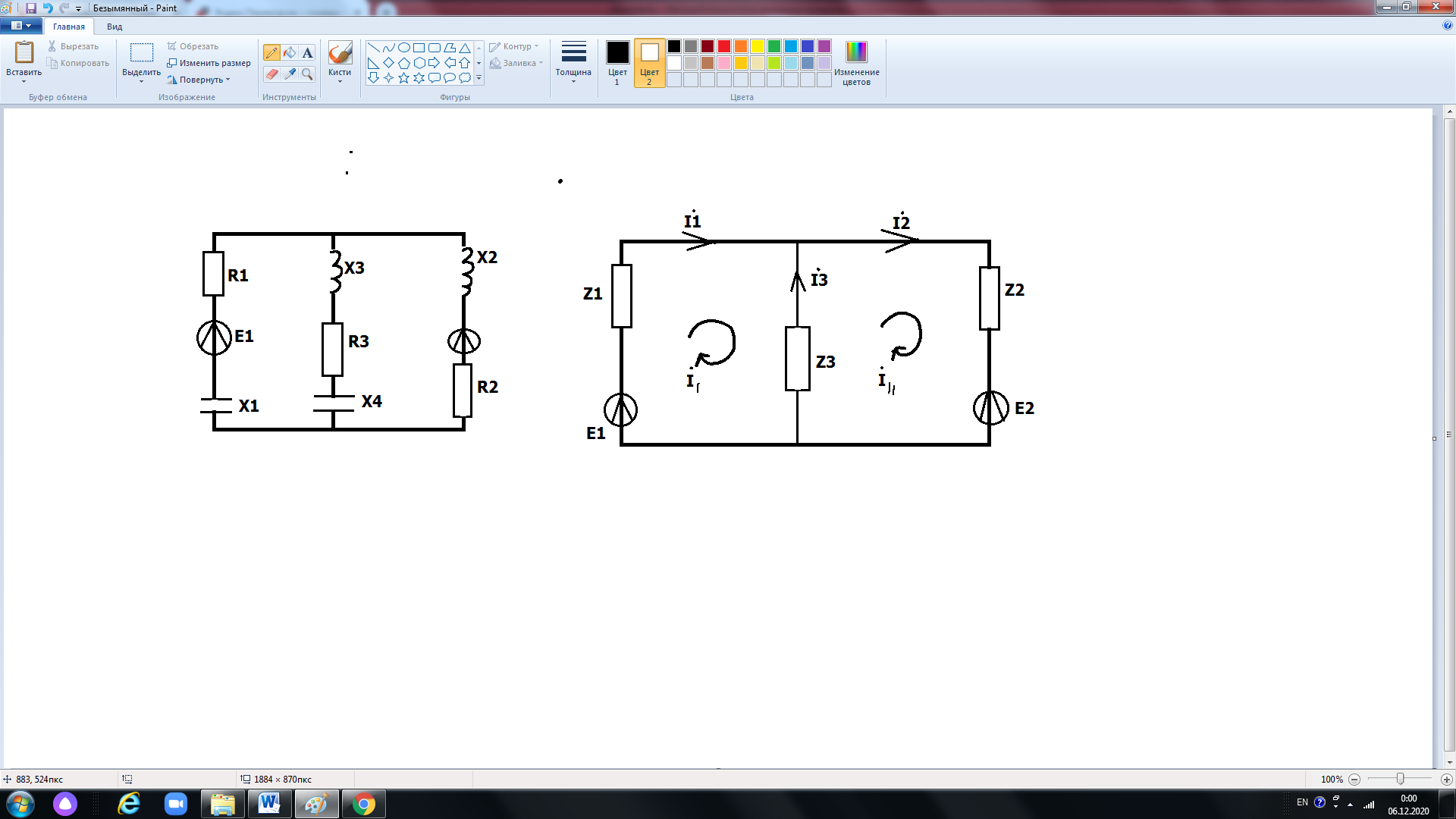
Сурет 29 – Контур бағыттары
Сұлбада екі іргелес контур бар. Сондықтан контур токтарының әдісіне сәйкес екі теңдеу жазамыз. Біз контурлық токтардың бағыттарын белгілейміз (тізбектерде оларды бірдей бағыттау ыңғайлы, мысалы, сағат тілімен) және Кирхгофтың екінші заңы бойынша теңдеулер құрастырамыз.
Бірінші контур бойынша кедергі:
Екінші контур бойынша кедергі:
1-ші 2 контурлар үшін іргелес тармақтың кедергісі
ЭҚК пен кедергілердің мәндерін қою арқылы:
Теңдеулер жүйесін АКТ қолдана отырып, теңдеулер жүйесін есептеу үшін «матрица» есептеу қажет.
Контурлы токтардың комплексін алгебралық формада жазамыз.
Мұндағы
және 
-
контурлық токтардың нақты құрамдастары:
Жақшаны ашатын болсақ
Комплексті сандардың белгілі қасиетін қолдана отырып, екі комплексті сан тең болады, егер олардың нақты және жорамал бөліктері сәйкесінше тең болса, онда біз теңдеулер жүйесін келесі түрде жазамыз:
Теңдеулер жүйесін шешу үшін компьютерде алынған коэффициенттерден матрица құрамыз. Матрицаның түрі:
| |  |  |  |  |
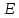| 15 | 20 | -5 | 12 | 190 |
| -20 | 15 | -12 | -5 | 110 |
| -5 | 12 | 20 | -20 | -110 |
| -12 | -5 | 20 | 20 | 190 |
Матрицаны ЭЕМ енгізу арқылы келесі нәтижені аламыз:
Токтың тармақтары контурлы токтармен байланысты:
токты анықтау үшін, үлкен модульдегі контурлы токтан 
-ден 
азайтамыз, және токты үлкен контурлы токқа бағыттаймыз .Токтың әсерлік мәндері:
Жауабы:
