Файл: Эффективные пути решения математических задач на уроках географии.docx

КОММУНАЛЬНОЕ ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ШКОЛА №16 ИМЕНИ Д.М.КАРБЫШЕВА ОТДЕЛА ОБРАЗОВАНИЯ ГОРОДА ТАРАЗ УПРАВЛЕНИЯ ОБРАЗОВАНИЯ АКИМАТА ЖАМБЫЛСКОЙ ОБЛАСТИ»

Доклад на тему «Эффективные пути решения математических задач на уроках географии»


Составил (-а) : Тучина Т.В.

Учитель географии сш № 16


Тараз-2022


Ум заключается не только в знаниях,
но и в умении использовать их на практике. Аристотель
Заданием современного школьного географического образования является осуществление переориентации ее целей на формирование таких жизненно важных компетенций школьников, которые способствовали бы их адаптации к активному участию в жизни общества, повышению уровня обучения, целеустремленной выработки практических умений и навыков.

Сегодня качество знаний определяется не столько тем, что знает и может воссоздать ученик, сколько тем, как он умеет воспользоваться своими знаниями. Слабым звеном учебных программ по естественным наукам в основной школе была перегруженность теоретическими знаниями и оторванность от практических умений в жизни. Как следствие, выпускники во многих жизненных ситуациях чувствуют себя беспомощными, поскольку их не научили или недостаточно закрепили умения применять полученные знания в жизни.

Современное школьное географическое образование предусматривает всестороннее развитие личности обучающихся с учетом их способностей, интересов и потребностей. Изменения, которые происходят в нашем государстве, требуют изменений и в уровне компетенций нынешних учащихся, которые станут гражданами нового государства. Знания, которые дает общеобразовательное учреждение, должны иметь большую практическую направленность.

Умение применять приобретенные знания на практике - важный показатель того, что ученики сознательно усвоили материал. Поэтому важно, чтобы в процессе изучения географии учитель акцентировал внимание учеников не только на теоретических вопросах, но и учил, использовать эти знания во время выполнения практических заданий, решения задач, работы с картами.

Математика и география – это две науки тесно связанные между собой. Математика позволяет определить обычные явления в природе, обществе, даже в нашем селе и в стране, которые основываются на приблизительных описаниях, на язык точных формул, которые можно получить не приблизительно, а точно. География складывается из всего окружающего: леса, океаны, пустыни, почва, общество, экономические отношения, животные и растения, климат и погода, круговорот веществ в природе и многое другое.

Каждая из цивилизаций, начиная с древнего мира, вырабатывала свои собственные, неповторимые пути познания мира, уникальные понятия, с помощью которых обдумывалось и излагалось полученное знание. Определить количество жителей, проживающих на определённой территории, рассчитать рельеф местности, измерить территорию, чтобы создать замечательное изобретение человечества- карту. «Рассчитать» - это главное слово, из всего выше сказанного.

Только с использованием «чисел», главного и основного орудия «царицы всех наук» - математики, можно познать одну из самых трудно-поддающихся изучению, науку Географию.

Составной частью современного образования и важным средством развития личности является географическое образование, существенная роль в котором отводится обучению решению различных задач, в том числе и расчетных. Умение решать расчетные задачи является одним из показателей уровня развития географического мышления учащихся, глубины усвоения ими учебного материала.

Некоторые учителя уделяют недостаточно внимания этому важному вопросу, сетуя на ограниченность времени, низкую мотивированность учащихся к решению подобных задач и их слабую математическую подготовку. В результате, как показывают олимпиады, единый государственный экзамен, учащиеся плохо справляются с решением расчетных географических задач или игнорируют их. Выход из положения – усиление дидактической роли расчетных географических задач и поиск новых подходов обучения их решению

Учебный предмет «география», изобилует большим количеством цифровых данных, которые нуждаются в правильной обработке и интерпретации. Изучение ряда тем школьного курса географии сопряжено с решением расчетных задач, под которыми условимся понимать задачи, требующие поиска необходимой величины, получения ее числового значения. В свою очередь, расчетные задачи в географии можно разделить на две группы :

• 
  расчетные задачи, требующие поиска числового значения характеристик физико-географических объектов, явлений или процессов (высоты полуденного Солнца, средней тем-пературы воздуха, амплитуды температур, уклона реки, падения реки и т. д.);
  

• 
  расчетные задачи, требующие поиска числового значения характеристик социально-экономических объектов, явлений или процессов (коэффициентов естественного прироста, смерт-ности, рождаемости, миграционного прироста, локализации, специализации и т. д.).
  

Обобщенный перечень расчетных географических задач представлен в Таблице 1.

Типовые расчетные географические задачи

№	Тема, раздел	Проверяемые умения	Пример формулировки задачи
	школьного курса
	географии
1	План и карта	Умение учащихся пользоваться масштабом,	Определите масштаб карты, если известно,
		определять расстояния на плане и карте, опре-	что расстояние в 80 км на ней показано отрез-
		делять масштаб карты, если известна площадь	ком в 2 см
		на карте и местности
2	Атмосфера	Умение определять атмосферное давление в	Атмосферное давление на вершине холма 740
		миллибарах, температуру воздуха, абсолют-	мм рт. ст., а температура воздуха –
		ную и относительную влажность воздуха,	8°С. Определите атмосферное давление у его
		коэффициент увлажнения, а также высоту,	подножия, если температура воздуха в состав-
		если известны температура и давление воздуха	ляет 12°С
3	Вращения Земли и	Умение определять географическую долготу	Определите точное время на Гринвичском
	их географические	по местному времени, и наоборот – рассчиты-	меридиане, если на 180° меридиане по мест-
	следствия	вать время при перемещении из одного часо-	ному времени 24 часа
		вого пояса (зоны) в другой
		Умение определять высоту полуденного	Определите полуденную высоту Солнца над
		Солнца по известной широте, и наоборот –	горизонтом в Ярославле на 15 число каждого
		время восходя и захода Солнца, продолжи-	месяца.
		тельность дня	Определите продолжительность дня, если
			известно что угол между точками восхода и
			захода на угломерном приборе составил 120q
4	Гидросфера	Умение определять уклон и падение реки,	Определите уклон реки, если известно, что
		вычислять содержание солей в океанической	исток находится на высоте 850 м, устье – 50 м
		воде или ее соленость	над уровнем моря, а длина реки составляет
			500 км
5	Население (мира,	Умение определять демографические показа-	Определите, на сколько и как изменилась чис-
	России)	тели (коэффициенты рождаемости, смертно-	ленность населения страны, если известно, что
		сти, естественного прироста, миграционный	на начало года она составляла 200 тыс. чел. В
		прирост) и на их основе вычислять изменение	течение года родилось 20 тыс. чел., умерло –
		численности населения территории	15 тыс. чел., выбыло из страны – 3 тыс. чел., а
			прибыло – 7 тыс. чел.
6	Хозяйство России,	Умение определять специализацию страны	Используя данные об объемах производства
	мира	(региона), долю отдельных отраслей в форми-	продукции и численности населения в Яро-
		ровании валового национального (региональ-	славской области и стране в целом, определи-
		ного) продукта, экспорте или импорте	те отрасли специализации региона
7	Ресурсы мира	Умения рассчитывать ресурсообеспеченность	Определите, на сколько лет (при сохранении
		территории	существующих тенденций добычи и уровня
			развития техники) в России хватит нефти,
			если ежегодно добывается 547 млн т, а ее за-
			пасы оцениваются в 14,1 млрд т

Так, уже в пятом классе идет речь об ориентировании на местности и определении сторон света с точностью до румбов, говорится о шаровидной форме Земли и представлении земной поверхности с помощью карт, однако работа с картами (масштаб, азимут) начинается в шестом классе. Пожалуй, именно эти понятия – первые, которые связывают географию и математику в школе. Для решения задач на определение расстояний и азимута по карте ученикам требуется математический навык работы с пропорциями и нахождения углов с помощью транспортира.

Задача 1. Определить название пункта А, для этого выяснить расстояние, направление и азимут при движении от пункта А до пункта В . по карте с помощью линейки и транспортира

Задача 1 решается в 6 классе с помощью линейки и транспортира. Такие задачи наверняка станут интереснее, если предложить учащимся карты местности, которая им знакома, или дать им возможность самостоятельно выбрать территории и объекты на топографической карте. Безусловно, задача поддается тиражированию и способствует знакомству учащихся с окружающим миром и краеведением.

В седьмом классе на уроках географии школьники, возможно, впервые встречаются с функциональными зависимостями и их графическим изображением – раньше, чем в математике. К примеру, суточное изменение температуры воздуха и зависимость температуры от высоты над поверхностью Земли. Здесь вполне уместны задачи на нахождение средних значений: среднесуточная, среднемесячная температура, причем возможно использование графика.

Кроме температуры, речь может идти об атмосферном давлении. Для решения таких задач ученикам необходимы навыки арифметических действий с десятичными дробями и умение разложить задачу на элементарные вычислительные шаги.

Задача 2. В годы Великой Отечественной войны над городом, временно оккупированном фашистами, несколько дней подряд кружились в воздухе листовки. Три дня фашистские дозорные следили за небом, пытаясь обнаружить в нем самолет, но безуспешно, самолета не было видно, а листовки продолжали опускаться на землю. Как потом выяснилось, один мальчик, по имени Саша, очень хотел помочь партизанам в борьбе с ненавистными гитлеровцами. Он пришел к ним и предложил свою помощь, рассказал, что придумал, как можно распространить листовки. И вот Саша взял листовки, сложил их стопкой в потухшей топке заводской трубы, которая имела высоту 30 метров. Листовки кружились в воздухе и медленно опускались на землю, их них люди узнавали правду о военных действиях Советской Армии.

Вопросы для обсуждения.

Объясните, какую закономерность использовал мальчик?

-Давайте еще раз вспомним, как изменяется давление с высотой, определите атмосферное давление на вершине трубы.

• 
  1) 30м:10,5м=2,9м
  
• 
  2) 760-3=757,1 мм рт. ст.
  
• 
  -Какую закономерность использовал Саша? (движение воздуха)
  
• 
  -Как движется воздух (из области высокого давления в область низкого- показать стрелкой на схеме)
  
• 
  -Аналогично воздух движется и в горизонтальном направлении. Так в чем же причина ветра (разница в атмосферном давлении)
  
• 
  -А почему возникает разница в давлении над земной поверхностью (из-за разницы в температуре)
  
• 
  -(Давайте вспомним теплый воздух какой?- (легкий), что с ним происходит? - (поднимается в верх), область какого давления образуется (НД), наоборот холодный воздух какой (тяжелый), что с ним происходит (скапливается в низу), что он делает (давит на земную поверхность), область с каким давлением образуется (ВД)
  

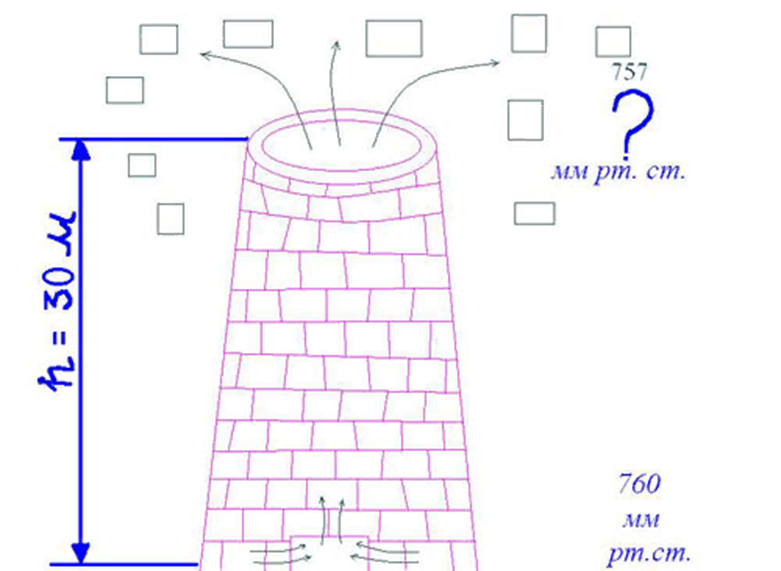
Рис.2. Иллюстрация к задаче 2

Задача 2 позволяет давать разные числовые данные и использовать информацию о местности и условиях, в которых проживают учащиеся. Учитывая наличие высотных домов в городах, можно задавать вопрос какое давление будет на N-ом этаже, если на первом 760 мм. рт. столба? На каком этаже давление будет равно 750 мм. рт. столба (1 этаж приблизительно равен 3 м. по высоте)?

Седьмой класс . Учебный материал изобилует числовой информацией: высоты и глубины географических объектов, длины рек и горных систем, площади островов и океанов и, конечно, географические координаты. Геометрические знания и навыки, которыми овладевают обучающиеся в 7 классе,

Задача 3. В Индийском океане произошло землетрясение (эпицентр имеет координаты 1⁰ ю.ш., 97⁰ в.д.), в результате которого возникли гигантские волны-цунами. Через какой промежуток времени цунами, достигнут одного из Мальдивских островов (1⁰ ю.ш., 72⁰ в.д.), если скорость их движения составляет 900 км/ч?

В шестом классе учащиеся впервые сталкиваются с понятием часовых поясов – ограниченных двумя меридианами частей земного шара шириной 15, в пределах которых время суток одинаково. С другой стороны, в каждой точке поверхности вводится солнечное (астрономическое) время – время на меридиане, проходящем через эту точку. Наконец, приводится карта часовых поясов, установленных на территории мира , и говорится про декретное время, которое на 1 час больше поясного. Совершенно уместны в этом случае задачи на местное время, правда, в них не учитывается карта часовых поясов. С точки зрения математики эти задачи просты: нужно только не забыть, что каждые 24 часа меняются сутки и помнить про линию перемены дат.

Задача 4. Задание. Томас и Акио познакомились на чемпионате мира по футболу. Акио живёт в столице Японии, а Томас — в столице Германии. Подростки общаются через Интернет, и при общении им приходится учитывать разницу во времени между их городами.
Часы на рисунках отображают время в городах, где живут подростки. Подпишите названия городов под соответствующими часами

В восьмом классе учащиеся знакомятся с задачами по экономической и социальной географии . Большой простор для задач математического содержания дает тема «Численность населения». Эти задачи связаны с такими понятиями естественный прирост (ЕП), миграционный прирост (МП), рождаемость (Р), смертность (С), коэффициенты рождаемости и смертности (Кр и Кс). Отдельно стоит отметить понятие промилле (‰) – количество тысячных долей, которое используется наряду с понятием процент (%). Так, коэффициент рождаемости измеряется в промилле: отношение числа родившихся к общей численности населения, умноженное на 1000.

В девятом классе решаем задачи на проценты по темам Миграция населения ,национальный состав ,Урбанизация

Задача 6 В стране с населением 18 млн человек и территорией 2724 тыс.км² городское население составляет 59%. Определите плотность сельского населения в этой стране и данную страну

В десятом и одиннадцатом классе решаем различные задачи по ресурсообеспеченности и загрязнеии окражающей среды

Задача 6

Исследование

Я исследовал, какое количество мусора выбрасывают жители нашего села за неделю. В эксперименте участвовало 10 семей моих одноклассников, количественный состав которых 2, 3, 4, 5 человек.

Результаты: Количество мусора выбрасываемого за неделю:

Семья из двух человек	5 килограмм
Семья из двух человек	10 килограмм
Семья из четырех человек	12 килограмм
Семья из трех человек	9 килограмм
Семья из трех человек	8 килограмм
Семья из пяти человек	15 килограмм
Семья из двух человек	4 килограмм
Семья из четырех человек	10 килограмм
Семья из трех человек	10 килограмм
Семья из четырех человек	13 килограмм

Выводы:

В результате за неделю10 семей выбрасывают 96 килограмм мусора.

Большую часть мусора составляют предметы из пластмассы (70%), на втором месте стеклянные и жестяные предметы (25%), и на третьем месте деревянные и бумажные (5%).

В среднем получается, что на одного человека в неделю приходится 3 кг. мусора. В месяц 12 кг. В год 156 кг. Это при условии ,что мы проживаем в селе и отходы от продуктов питания уходят на корм домашних животных, собираем макулатуру и жестяные банки из под консервированных продуктов.

Это мы делаем чтобы мусорных отходов стало меньше. И улучшилась экология села.

Задачи позволяют генерировать различные модификации, причем привязывать их к определенной местности, группе людей, явлениям природы , связанных с реальной жизнью наших учеников. Таким образом, каждая из приведенных выше задач

может рассматриваться как опорная для множества задач на данную тему. При этом задачи становятся интереснее для учащихся, если привязывать их к региону проживания учащихся либо к достопримечательным географическим объектам.

Задачи стимулируют продуктивную учебную деятельность, формируют познавательный интерес и развивают интеллектуальные и творческие способности.

Использование задач математического содержания на уроках географии разовьет не только географические компетенции учащихся, но и их математические навыки, стимулируя поисковую и познавательную активность учащихся, способствует формированию практических умений. Систематическое решение географических задач является важным шагом в подготовке учеников к ГИА , ЕНТ и олимпиадам по предмету.