№	Задания
1	Найдите ве­ли­чи­ну угла DOK, если OK — бис­сек­три­са угла AOD, ∠DOB = 108°. Ответ дайте в градусах.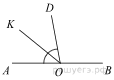
2	Найдите гра­дус­ную меру центрального ∠MON, если известно, NP — диаметр, а гра­дус­ная мера ∠MNP равна 18°.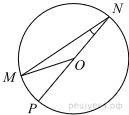
3	Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.
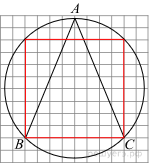
4	Найдите угол ABC. Ответ дайте в градусах.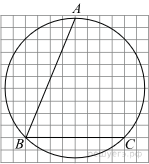
5	Укажите но­ме­ра верных утверждений.   1) Бис­сек­три­са равнобедренного треугольника, проведённая из вершины, про­ти­во­ле­жа­щей основанию, делит ос­но­ва­ние на две рав­ные части. 2) В любом пря­мо­уголь­ни­ке диагонали вза­им­но перпендикулярны. 3) Для точки, ле­жа­щей на окружности, рас­сто­я­ние до цен­тра окружности равно радиусу.   Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.
6	Медиана равностороннего треугольника равна 9√3. Найдите сторону этого треугольника.
7	Найдите гра­дус­ную меру ∠ACB, если известно, что BC яв­ля­ет­ся диа­мет­ром окружности, а гра­дус­ная мера центрального ∠AOC равна 96°.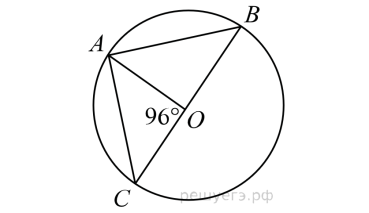

Ответы:

1. 
   36
   
2. 
   144
   
3. 
   1600
   
4. 
   67,5
   
5. 
   13
   
6. 
   18
   
7. 
   42
   

Решение:

1. Углы AOD и DOB — смежные, вместе составаляют развёрнутый угол, следовательно, ∠

---

AOD = 180° − ∠DOB = 180° − 108° = 72°. Поскольку OK — биссектриса угла AOD, ∠AOK = ∠KOD = ∠AOD/2 = 72°/2 = 36°.

 

Ответ: 36.

2. Треугольник MON — равнобедренный. Тогда ∠MON = 180° − 2·18° = 144°.

 

Ответ: 144.

3. Все стороны квадрата равны, поэтому сторона длина стороны квадрата равна 160:4=40. Найдём площадь квадрата как квадрат его стороны: S=40²=1600

 

Ответ: 1600.

4. Проведём вспомогательное построение. Заметим, что дуга BC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°. Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги BC: 90°/2 = 45°. Треугольник ABC — равнобедренный, следовательно,:

 


 

 

 

Ответ: 67,5.

5. Проверим каждое из утверждений.

1) «Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части» — верно по свойству равнобедренного треугольника.

2) «В любом прямоугольнике диагонали взаимно перпендикулярны» — неверно, это утверждение справедливо исключительно для ромба, а не для прямоугольника.

3) «Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу» — верно, т. к. окружность — множество точек, находящихся на заданном расстоянии от данной точки.

 

Ответ: 13.

6. . Так как треугольник АВС равносторонний, то его медиана BH является и биссектрисой, и высотой. Тогда треугольник ABH - прямоугольный. Тогда:

 



 

 

Ответ: 18

7. Так как ∠AOC и ∠AOB — смежные, ∠AOB = 84°. Центральный угол равен дуге на которую он опирается, поэтому градусная мера дуги AB равна 84°. Угол ACB — вписанный и равен половине дуги, на которую опирается, поэтому ∠

---

ACB = 42°.

 

Ответ: 42.

---

Смотрите также файлы

• Проекты Проекты по литературе Подготовили ученицы 5 б класса Горшенина Алла Томакова Дарья Учитель.ppt

• Семинар 14. Народная игровая культура как педагогическое явление.rtf

• Более детально расписаны требования к условиям реализации программы общего образования, в том числе обеспечивающие формирование функциональной грамотности новый вид общесистемные требования.docx

• Экономическими моделями.docx

• !Сйытар мен газдарды озалысы туралы ылымгидромеханика задарымен жылдамдыты анытайтын процестер.docx