КВАДРАТ
a d	Определение Квадрат – это прямоугольник, у которого все стороны равны.
a – сторона d - диагональ P = 4a –периметр – сторона ч/з периметр S = a2– площадь ч/з сторону – площадь ч/з диагональ	Свойства: 1) противоположные стороны равны; 2) противоположные углы равны; 3) диагонали точкой пересечения делятся пополам; 4) диагонали равны; 5) диагонали взаимно перпендикулярны; 6) диагонали делят углы пополам

ПРЯМОУГОЛЬНИК
b a d	Определение Прямоугольник – параллелограмм, у которого все углы прямые.
a – длина b- ширина d - диагональ P = 2(a+b)- периметр S = ab- площадь ,  - угол м/у диагоналями	Свойства: 1) противолежащие стороны равны; 2) противолежащие углы равны; 3) диагонали точкой пересечения делятся пополам; 4) сумма углов, прилежащих к одной стороне равна 180; 5) диагонали равны.
Если в параллелограмме хотя бы один угол прямой, то он является прямоугольником.	Если в параллелограмме сумма двух противоположных углов равна 180 - это прямоугольник.
В четырехугольнике, в котором три угла прямые – прямоугольник.	Если биссектриса прямоугольника делит пополам сторону, которую она пересекает, то одна из сторон прямоугольника в два раза больше другой его стороны.
Если все углы четырехугольника равны – это прямоугольник.	Если в четырехугольнике диагонали равны и в точке пересечения делятся пополам, то такой четырехугольник – прямоугольник.

---

ПАРАЛЛЕЛОГРАММ
b a 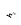h1 a, b – стороны h1, h2 – высоты	Определение Параллелограмм – это четырехугольник, противолежащие стороны которого попарно параллельны.
P S = a b sin- площадь = 2(a+b)- периметр - площадь	Свойства: 1) противолежащие стороны равны; 2) противолежащие углы равны; 3) диагонали точкой пересечения делятся пополам; 4) сумма углов, прилежащих к одной стороне равна 180.
b  a
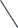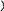 d1 d2  - угол м/у диагоналями S =	Признаки: 1) Если две противолежащие стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм. 2) Если противолежащие стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм. 3) Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм. 4) Если в четырехугольнике сумма углов, прилежащих к каждой из двух смежных сторон равна 180, то этот четырехугольник — параллелограмм. 5) Если противоположные углы четырехугольника равны, то такой четырехугольник – параллелограмм
Любой отрезок с концами на противолежащих сторонах параллелограмма, проходящий через точку пересечения его диагоналей, делится этой точкой пополам.
Биссектрисы двух соседних углов параллелограмма перпендикулярны
Биссектрисы двух противолежащих углов параллельны или лежат на одной прямой.
Угол между высотами параллелограмма, проведенными из одной вершины, равен углу параллелограмма при соседней вершине.

---

Как действовать

1. 
   Чтобы установить, что четырехугольник – параллелограмм, докажите, что в нем:
   

ЛИБО 1) противоположные стороны попарно параллельны (определение параллелограмма);

2) противоположные стороны попарно равны (признак);

3) две противоположные стороны равны и параллельны (признак);

4) диагонали точкой их пересечения делятся пополам (признак).

2. 
   Для того, чтобы установить, что данный параллелограмм – прямоугольник, докажите, что у него:
   

ЛИБО 1) все его углы прямые (определение прямоугольника);

2) диагонали равны (признак).

3. 
   Для утверждения, что четырехугольник является прямоугольником, докажите, что:
   

ЛИБО 1) этот четырехугольник – параллелограмм, а параллелограмм - прямоугольник;

2) три угла четырехугольника – прямые.

Р a – сторона h – высота  - угол ромба P = 4a –периметр S = a2 sin ОМБ
a 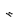 d1, d2–диагонали 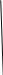d1 d2	Определение Ромб – это параллелограмм, в котором все стороны равны. Свойства: 1) противолежащие стороны равны; 2) противолежащие углы равны; 3) диагонали точкой пересечения делятся пополам; 4) сумма углов, прилежащих к одной стороне равна 180; 5) диагонали взаимно перпендикулярны; 6) диагонали делят углы пополам.
	Признак: Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм – ромб.
Диагональ ромба разделяет его на два равных треугольника.	Диагонали ромба разделяют его на четыре равных прямоугольных треугольника.
Ромб, в котором один угол nрямой,- квадрат	Четырёхугольник, все стороны которого равны, является ромбом.
Параллелограмм, диагонали которого делят углы пополам, - ромб.

---

Как действовать

Чтобы установить, что данный параллелограмм - ромб, докажите ,что в нем:

ЛИБО 1) все стороны равны (определение ромба);

2) диагонали взаимно перпендикулярны (признак);

Т a РАПЕЦИЯ
b h	Определение Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие – не параллельны.
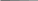m a, b – основания трапеции h – высота m – средняя линия	Средняя линия трапеции – это отрезок, соединяющий середины её боковых сторон. Свойство средней линии трапеции: Средняя линия трапеции параллельна основаниям и равна их полусумме.
	ПРЯМОУГОЛЬНАЯ ТРАПЕЦИЯ– трапеция, в которой одна из боковых сторон перпендикулярна основаниям (или один угол равен 90)
Сумма градусных мер двух углов трапеции. Прилежащих к боковой стороне, равна 180.	РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ– трапеция, в которой боковые стороны равны. Свойство: углы при основании равны; диагонали равнобедренной трапеции равны. диагонали образуют с ее основанием равные углы Признак: Если в трапеции углы при основании равны, то такая трапеция является равнобедренной.
Если боковая сторона трапеции равна меньшему основанию, то диагональ, соединяющая их концы, - биссектриса угла, прилежащего к большему основанию.
Если диагонали трапеции взаимно перпендикулярны, то средняя линия трапеции равна ее высоте.
Отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности.	В равнобедренной трапеции сумма противолежащих углов равна 180
	Если в трапеции сумма противоположных углов равна 180, то трапеция равнобедренная

---

Как действовать

Если в условии задачи дана трапеция, то полезно такое дополнительное построение: проведите через вершину трапеции прямую, параллельную боковой стороне, и используйте свойства полученных параллелограмма и треугольника.

---

Смотрите также файлы

• Электролитическая диссоциация (ЭД) Способность проводить электрический ток.ppt

• Водоросли 5 класс.docx

• Урока однкнр Взросление человека в культуре народов России.docx

• Учёный Его вклад в развитие биологии.docx

• Новости Статьи.pdf