Файл: Методические рекомендации по выполнению практических работ по учебной дисциплине математика для профессий.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 46

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство образования и науки Хабаровского края

Краевое государственное бюджетное образовательное учреждение

«Профессиональный электротехнический лицей № 7»
МАТЕМАТИКА
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ

МНОГОГРАННИКИ

ПРИЗМА




Хабаровск

2017г.

Одобрены

на заседании МС

общеобразовательных

дисциплин

председатель МС

_________________ Ильин П.В.

« »______________2017 г.





Методические рекомендации по выполнению практических работ по учебной дисциплине «МАТЕМАТИКА» для профессий:
09.01.02 Наладчик компьютерных сетей;

13.01.05 Электромонтер по техническому обслуживанию электростанций и сетей;

13.01.10 Электромонтер по ремонту и обслуживанию электрооборудования (по отраслям).

270843.04 Электромонтажник электрических сетей и электрооборудования

Организация-разработчик: КГБПОУ «Профессиональный электротехнический лицей № 7»
Разработчики: Канова В.М. – преподаватель математики
Рецензенты:

СОДЕРЖАНИЕ

Пояснительная записка
…………………………………………………………………..Стр. 4

Практическая работа №2
…………………………………………………………….Стр. 5 – 13

Список литературы
…………………………………………………………………Стр. 14


ПОЯСНИТЕЛЬНАЯ ЗАПИСКА



Цель изучения дисциплины «МАТЕМАТИКА»

  • развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления;

  • овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения смежных естественно - научных дисциплин на базовом уровне и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

  • воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.

Ведущей дидактической целью практических занятий является формирование практических умений вычислять площади и объемы многогранников.

В соответствии с ведущей дидактической целью содержанием практических занятий является:

  • повторение теоретического материала;

  • выполнение тренировочных упражнений;

  • выполнение практической работы по образцу.


Данное пособие содержит методические указания по выполнению практических работ по дисциплине «МАТЕМАТИКА». Пособие рассчитано на 3 часа практических занятий. В каждой теме дана краткая теоретическая информация по теме, порядок выполнения типовых действий по образцу.

ПРАКТИЧЕСКАЯ РАБОТА. ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЕМ ПРИЗМЫ.
Цель: закрепить навыки решения практических задач на вычисление площади поверхности и объема призмы.
Теоретическая часть:




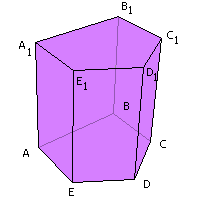
Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.
Грани призмы, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами.

Все боковые ребра равны между собой как параллельные отрезки, ограниченные двумя параллельными плоскостями. Все боковые грани призмы являются параллелограммами.
Высота призмы — это расстояние между ее основаниями. Для прямой призмы, у которой все ребра перпендикулярны основаниям, — это любое из ребер.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы.

Прямой призмой называется призма, у которой боковое ребро перпендикулярно плоскости основания.




Правильной призмой называется прямая призма, основанием которой является правильный многоугольник.




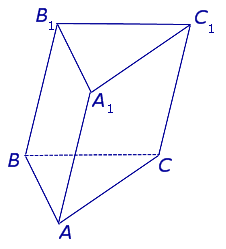Наклонной называют такую призму, боковые ребра которой не будут перпендикулярны к основаниям.





Призма, основанием которой является параллелограмм, называется параллелепипедом.



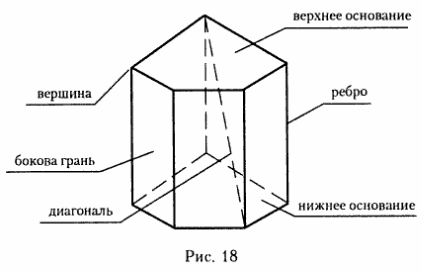
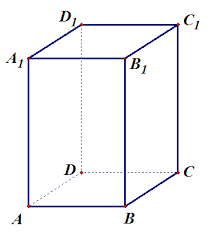
На рис. 1 — пятигранная прямоугольная призма (в основании призмы лежит пятиугольник). У нее 10 вершин; 5 боковых граней; 2 основания (верхнее и нижнее). Для прямоугольной призмы высотой служит любое ребро, расположенное перпендикулярно основанию.



Рис. 1.

Разверткой призмы называется перенос без искажения размеров всех ее граней в одну плоскость. Развертка призмы, приведена на рис. 2.

Рис. 2.
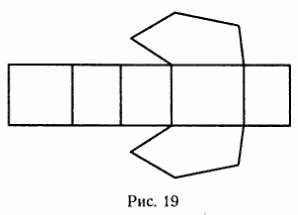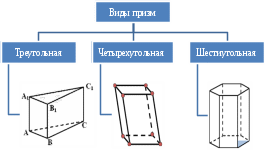
Н а рис. 2 прямоугольник, разделенный ребрами на 5 меньших прямоугольников, составляет развертку боковой поверхности, а сверху и снизу от нее расположены многоугольники верхнего и нижнего оснований. Площадь всей этой фигуры и составит полную площадь поверхности призмы.


В зависимости от числа углов в основании призма называется треугольной, четырёхугольной, пятиугольной и т. д.

На рисунках 3, 4, 5 даны изображения и развёртки правильных призм: треугольной, четырёхугольной и шестиугольной.


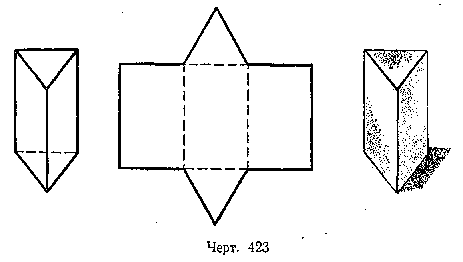
Рис. 3.



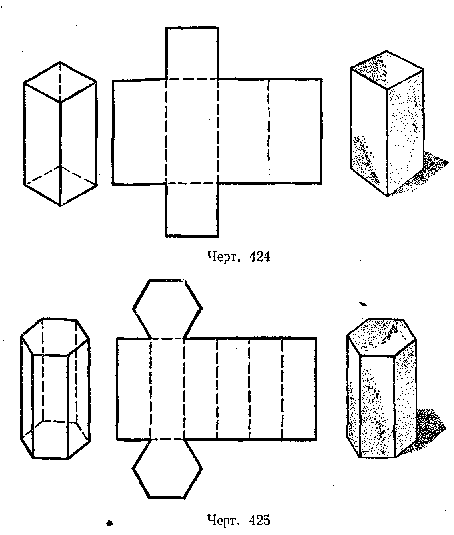
Рис. 4.



Рис. 5.

Боковыми гранями любой правильной призмы служат прямоугольники.
Определение. Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью ее боковой поверхности призмы – сумма площадей боковых граней.

Площадь Sполн полной поверхности выражается через площадь Sбок боковой поверхности и площадь Sосн основания призмы формулой:




Sполн = Sбок + 2Sосн.,
где Sполн – площадь полной поверхности,

Sбок
– площадь боковой поверхности,

Sосн.- площадь основания
Теорема: Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Sбок = ·h
где Sбок — площадь боковой поверхности

 — периметр основания призмы (многоугольника, лежащего в основании);
h — высота призмы (для прямоугольной — это длина бокового ребра призмы).








Формулы для нахождения площадей фигур



Прямоугольник: S = a·b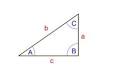


Прямоугольный треугольник: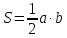



Квадрат: S = a2


Равнобедренная трапеция: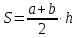



Равносторонний треугольник: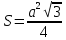



Равнобедренный треугольник: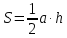



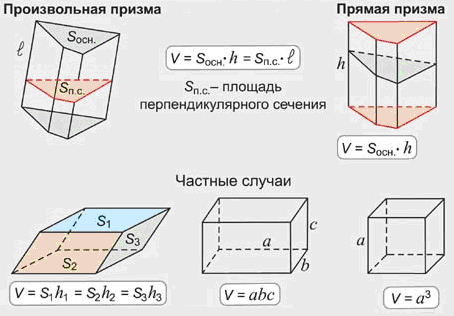
Определение. Объем прямой призмы
 равен произведению площади основания на высоту призмы.

V = Sосн.h
где: V — объем призмы;
Sосн. — площадь основания призмы (многоугольника, лежащего в основании призмы);

h — высота призмы (для прямоугольной - длина бокового ребра призмы).
Упражнения:

  1. Прямая призма в основании имеет квадрат со стороной 6 см. Высота призмы 12 см. Чему равна площадь полной и боковой поверхностей этой призмы?




  1. В основании прямой призмы лежит треугольник со сторонами 3см, 4см и 5см, высота призмы равна 5см. Чему равна площадь боковой поверхности этой призмы?




  1. Основание прямой призмы является прямоугольный треугольник со сторонами АС = 10 см, АВ = 6 см. Высота ВВ1 = 9 см. Найдите площадь полной и боковой поверхностей, и объем прямой призмы.

Образец выполнения работы.

Пример 1: Прямая призма в основании имеет квадрат со стороной 3 см. Высота призмы 6 см. Чему равна площадь полной и боковой поверхностей этой призмы?

Дано:

Решение:

ABCDA1B1C1D1 - прямая призма

ABCD – квадрат

AB = 3 см

h = 6 см

Sбок. - ?

Sполн - ?



Sп.п. = Sбок +2Sосн

Sбок = h = АА1 (прямая призма).

Так как в основании прямой призмы лежит квадрат, то

= 4·АВ

= = 4·3 = 12 см

Sбок = 12·6 = 72 см2

Sосн = а2 = 32 = 9 см2

Sполн = 72 + 2·9 = 90 см2




Ответ: Sполн = 90 см2, Sбок = 72 см2

Смотрите также файлы