Файл: Методические рекомендации по выполнению практических работ по учебной дисциплине математика для профессий.docx
Добавлен: 12.12.2023
Просмотров: 43
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
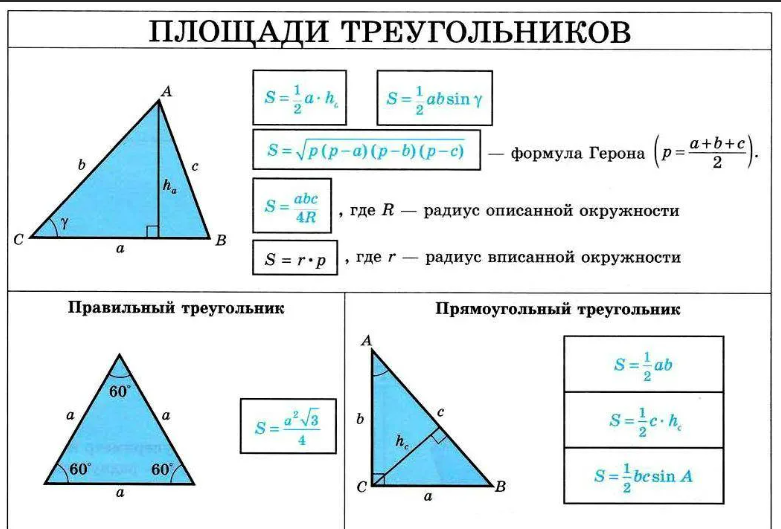
Пример 2: В основании прямой призмы лежит треугольник со сторонами 2см, 3см и 4см, высота призмы равна 4см. Чему равна площадь боковой поверхности этой призмы?
 Дано: Дано: | Решение: | |
| ABCA1B1C1 - прямая призма ABC – треугольник AB = 2 см BC = 3см AC = 4 см h = 4 см  | Sбок =  h = h =  АА1 (прямая призма). АА1 (прямая призма).  = АВ +ВС+АС = АВ +ВС+АС = 2+3+4 = 9 см = 2+3+4 = 9 смSбок =9·4 = 36 см2 | 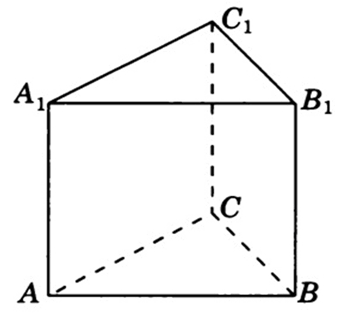 |
| Sбок. - ? | | |
| Ответ: Sбок = 36 см2 | | |
Пример 3: Основание прямой призмы является прямоугольный треугольник со сторонами АС = 25 см, АВ = 7 см, высота ВВ1 = 9 см. Найдите площадь полной и боковой поверхностей, и объем прямой призмы.
 Дано: Дано: | Решение: | |
| ABCDA1B1C1D1 – прямая призма ABC – прямоугольный треугольник АС = 25 см ВС = 7 см  ВВ1 = 5 см ВВ1 = 5 см Sбок - ? Sп.п. - ?  - ? - ? | Sп.п.= Sбок +2Sосн Sбок =  ·h = ·h =  ·АА1 (прямая призма). ·АА1 (прямая призма). = АВ+ВС+АС = АВ+ВС+АСРассмотрим ∆ АВС – прямоугольный треугольник По теореме Пифагора: АС2 = АВ2 +ВС2 ВС2 = АС2 - АВ2 ВC = 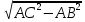 ВC = 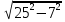 = = 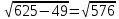 = 24 см = 24 см = 25+7+24 = 56 см = 25+7+24 = 56 смSбок =24·5 = 120 см2 Sосн = 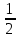 · АВ·ВС · АВ·ВСSосн = 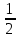 ·7·24 = 84 см2 ·7·24 = 84 см2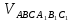 = Sосн ·h = Sосн ·h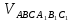 = 84+5 = 420 см3 = 84+5 = 420 см3 |     5 ? 7 25     ? 7 25 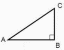 |
| Ответ: Sбок =120 см2; Sосн = 84 см2; 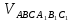 = 420 см3 = 420 см3 | ||
Вариант 1
Все задания выполняются в ТЕТРАДИ
Часть А
-
Многогранник, который состоит из двух плоских многоугольников, совмещенных параллельным переносом, называется:
-
пирамидой -
призмой -
цилиндром -
параллелепипедом
-
Если боковые ребра призмы перпендикулярны основанию, то призма является:
-
наклонной -
правильной -
прямой -
выпуклой
-
Если в основании призмы лежит параллелограмм, то она является:
-
правильной призмой -
параллелепипедом -
правильным многоугольником -
пирамидой
-
Сколько граней имеет шестиугольная призма?
-
6 -
8 -
10 -
4
-
Сколько ребер имеет семиугольная призма
-
21 -
18 -
15 -
12
Часть В. Оформление 2, 3 (чертеж, буквенные обозначения, дано, найти, решение, формулы)
-
Какое наименьшее число граней, ребер, вершин может иметь призма?
Ответ:______________________________
-
Прямая призма в основании имеет квадрат со стороной 6 см. Высота призмы 12 см. Чему равна площадь боковой поверхности этой призмы?
-
Основание прямой призмы является прямоугольный треугольник со сторонами АС = 10 см, АВ = 6 см. Высота ВВ1 = 15 см. Найдите площадь полной и боковой поверхностей, и объем прямой призмы.
Часть С. Оформление (чертеж, буквенные обозначения, дано, найти, решение, формулы)
-
В основании прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120° между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите площадь боковой поверхности призмы.
Вариант 2
Все задания выполняются в ТЕТРАДИ
Часть А
-
Многогранник, который состоит из двух плоских многоугольников, совмещенных параллельным переносом, называется:
-
пирамидой -
призмой -
цилиндром -
параллелепипедом
-
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
-
диагональю -
ребром -
гранью -
осью
-
У призмы боковые ребра: равны
-
симметричны -
параллельны и равны -
параллельны -
симметричны и параллельны
-
Сколько ребер имеет шестиугольная призма ребер
-
6 -
10 -
18 -
15
-
Сколько граней имеет семиугольная призма
-
5 -
8 -
9 -
10
Часть В. Оформление 2, 3 (чертеж, буквенные обозначения, дано, найти, решение, формулы)
-
Какое наименьшее число граней, ребер, вершин может иметь призма?
Ответ:_________________________
-
В основании прямой призмы лежит треугольник со сторонами 3см, 4см и 5см, высота призмы равна 5см. Чему равна площадь боковой поверхности этой призмы?
-
Основание прямой призмы является прямоугольный треугольник со сторонами АС = 10 см, АВ = 6 см. Высота ВВ1 = 10 см. Найдите площадь полной и боковой поверхностей, и объем прямой призмы.
Часть С. Оформление (чертеж, буквенные обозначения, дано, найти, решение, формулы)
-
В основании прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120° между ними. Наибольшая из площадей боковых граней равна 55 см2. Найдите площадь боковой поверхности призмы.
Расчетное время выполнения практической работы: 45 минут
Контрольная работа оценивается по 14 – бальной системе.
Максимальное количество баллов по заданиям:
Часть А
Задание 1 - 1 балл
Задание 2 - 1 балл
Задание 3 - 1 балл
Задание 4 - 1 балл
Задание 5 – 1 балл
Часть В
Задание 1 - 2 балла
Задание 2 - 2 балла
Задание 3 - 2 балла
Часть С
Задание 1 - 3 балла
Шкала перевода баллов в отметки по 5 – бальной системе
12 – 14 баллов – 5
11 –9 баллов – 4
8 – 6 баллов – 3
5 и меньше баллов – 2
Ответы и критерии оценки знаний.
| | Вариант 1 | Вариант 2 |
| Часть А | ||
| 1 | А | А |
| 2 | В | А |
| 3 | Б | В |
| 4 | Б | В |
| 5 | А | В |
| Часть В | ||
| 1 | Вершин 6, ребер 9, граней 5 | Вершин 6, ребер 9, граней 5 |
| 2 | 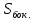 = 288 см2 = 288 см2 | 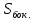 = 60 см2 = 60 см2 |
| 3 | 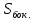 = 360 см2; = 360 см2; 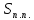 = 408 см2; = 408 см2; = 360 см3. = 360 см3. | 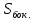 = 240 см2; = 240 см2; 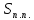 = 288 см2; = 288 см2; = 240 см3. = 240 см3. |
| Часть С | ||
| 1 | 77 см2 | 121 см2 |
СПИСОК ЛИТЕРАТУРЫ
Основные источники:
-
Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия 10-11 (базовый и профильный уровни) – М.: Просвещение, 2008. – 206с. -
М.И.Башмаков Математика: учебник для учреждений нач. и сред. Проф. образования – М.: Академия, 2012. – 302с. -
Алгебра и начала анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни – М.: Просвещение, 2010. – 336с.
Дополнительные источники:
-
В.А. Гусев, С.Г. Григорьев, С.В. Иволгина Математика для профессий и специальностей социально – экономического профиля: учебник для образовательных учреждений нач. и сред. проф. образования – М.: Академия, 2012. – 384с. -
С.Г. Григорьев, С.В. Математика для образоват. учреждений сред. проф. образования. – М.: Академия, 2012. – 376с.