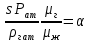(13)

Очевидно, 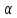– безразмерная величина.

Тогда выражение для газового фактора можно записать так:

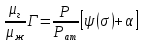(14)

При установившемся движении газовый фактор всюду в пласте будет одинаков. Все изложенное выше преследовало одну цель —установить связь между давлением и насыщенностью, чего мы и добились. Обозначим:

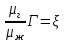(15)

При Г = const 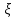также постоянно, тогда из этого следует:

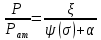(16)

Обозначим:

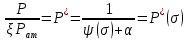(17)

где 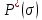- известная функция насыщенности.

График зависимости 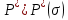может быть легко построен по исходным кривым фазовых проницаемостей и по последней формуле. Он имеет примерно вид, показанный на рисунке: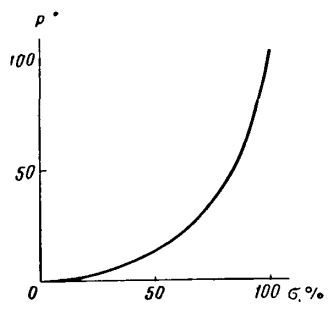



Рисунок 4. Зависимость

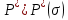
При расчетах стационарного движения газированной нефти наиболее интересной величиной является — расход жидкости. Поскольку газовый фактор известен, согласно формуле 10 определяем расход газа: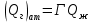

(18)

Формулу для , учитывая относительную проницаемость можно представить в виде: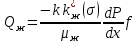

(19)

В этом уравнении 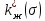— известная функция насыщенности и, кроме того, как мы видели, давление 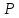— также однозначная.

Таким образом, насыщенность является параметром, связывающим зависимости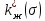

---

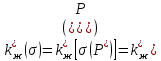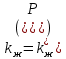и . Зная эти зависимости из рисунка относительных фазовых проницаемостей для газированной жидкости и функции насыщенности легко построить зависимость , т. е. связать фазовую проницаемость c давлением . График зависимости представлен на рисунке: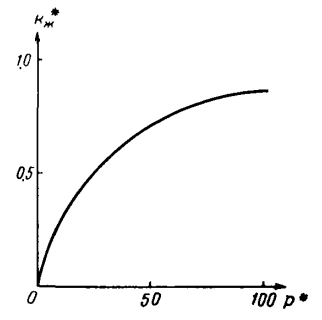



Рисунок 5. Зависимость

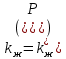
Теперь, когда установлена однозначная зависимость 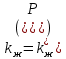, вводим новую функцию Н, полный дифференциал которой равен 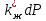. Эта функция имеет размерность давления и называется функцией Христиановича:

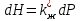(20)

Теперь уравнение для дебита жидкости можно записать так:

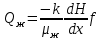(21)

Данное уравнение ничем не отличается от обычного закона Дарси, но только роль давления играет функция Н.

Следовательно, для установившегося движения газированной жидкости сохраняются все формулы для движения однородной несжимаемой жидкости с заменой давления на функцию Христиановича.

Функция Христиановича Н определяется из уравнения:

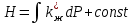(22)

Для вычисления функции Н можно поступить следующим образом:

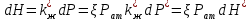(23)

где дифференциал безразмерной функции 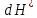равен:

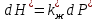(24)

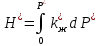(25)

Зависимость 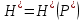строится по графику зависимости 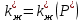графическим интегрированием по вышеуказанному уравнению. Она была впервые построена Бернардом Борисовичем Лапуком и имеет вид:

---

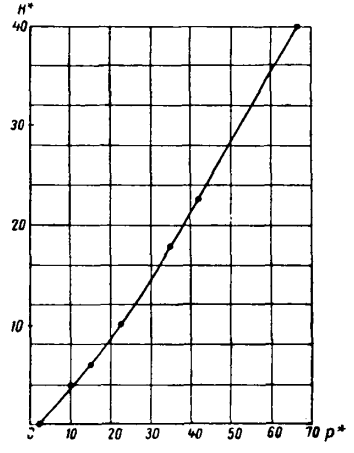
Рисунок 6. График зависимости

Константин Алексеевич Царевич составил подробные таблицы, позволяющие определить значения функции 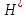при разных значениях для сцементированных и несцементированных песков.

Таким образом, получаем возможность использовать при расчетах стационарного движения газированной нефти все формулы для движения однородной несжимаемой жидкости, в которых давление должно быть заменено функцией Христиановича 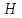. Получаем:

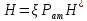(26)

Например, дебит жидкости из скважины, находящейся в центре кругового пласта, равен согласно формуле Дюпюи:

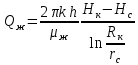(27)

Функция 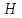здесь будет распределена так же, как давление при фильтрации однородной несжимаемой жидкости: для радиального движения — по закону логарифмической кривой, для прямолинейного движения — по линейному закону.

Последовательность расчетов такова. Зная контурные давления 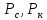и газовый фактор Г, по формуле 17 находят 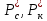и затем из графика 6 находят , .

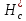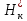Зная 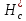, , 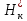из уравнения 26 находят 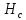, , 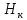после чего все элементы движения определяются без затруднений. Для ускорения и облегчения расчетов можно также воспользоваться таблицами К. А. Царевича.

Эту трудоемкую методику расчетов можно упростить. Обратим внимание, что в широком диапазоне зависимость

---

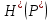
линейная, т. е.:

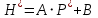(28)

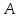где и 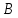– постоянные.

Параметр А является угловым коэффициентом прямой, В — свободным членом.

Разность 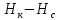можно выразить через разность давлений:

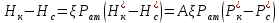(29)

или учитывая уравнение 28:

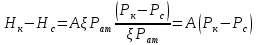(30)

Формула показывает, что для приближенных расчетов газированную жидкость можно рассматривать как фиктивную однородную несжимаемую жидкость. Из графика

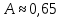
Тогда формула Дюпюи примет вид:

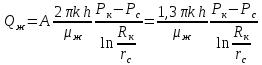(31)

В дальнейшем прием сведения установившегося движения газированной жидкости к движению фиктивной однородной несжимаемой жидкости М. М. Глоговским и М. Д. Розенбергом был использован и развит. Ими было показано, что параметр 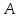в довольно широких пределах удовлетворительно описывается формулой:

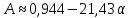, (32)

где

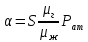
При этом предполагается условие:

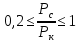(33)

Таким образом, практические расчеты стационарного движения газированной жидкости можно производить, пользуясь этой заменой, что чрезвычайно облегчает их выполнение.

1.2 НЕУСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ГАЗИРОВАННОЙ ЖИДКОСТИ.

Неустановившееся движение газированной жидкости является наименее разработанной задачей. Некоторые авторы решают ее методом материального баланса, связывая среднее пластовое давление с насыщенностью и отбором из всего месторождения в целом.

В основе метода материального баланса лежит закон сохранения материи, который применительно к залежам углеводородов формулируется следующим образом: количество углеводородов, находящихся в залежи до начала разработки, равно количеству извлеченных и оставшихся в залежи углеводородов на любую произвольную дату разработки.

---

Запасы нефти, содержащиеся в залежи, подсчитываются с учетом изменения основных показателей разработки, физических свойств нефти, воды и породы в зависимости от снижения давления в процессе разработки залежи. Добыча нефти, растворенного газа и воды, закачка воды и газа в залежь вызывают непрерывное перераспределение флюидов вследствие изменения пластового давления. При этом баланс между количеством УВ, содержавшихся в залежи до начала разработки, и количеством УВ, извлеченных и оставшихся на момент разработки, не нарушается.

При этом рассмотрении исключается роль скважин. Между тем знание поведения скважины является весьма важным, например связь дебита при нестационарном режиме с забойным давлением и т. д. Ряд существенно важных результатов, основанных на применении метода последовательной смены стационарных состояний, был получен К. А. Царевичем.

К. А. Царевич решил задачу об истощении месторождения, которое эксплуатировалось при режиме растворенного газа. При этом месторождение рассматривалось как замкнутый нефтяной подземный резервуар, где давление первоначально равно давлению насыщения. Резервуар вскрывался скважиной, и начинался отбор жидкости.

К. А. Царевич исследовал вторую фазу нестационарного движения, когда условная воронка депрессии дошла до границ резервуара и начиналось истощение залежи в целом.

Аналогичные расчеты методом конечных разностей выполнил В. А. Архангельский и получил очень сходные результаты. Эти результаты кратко заключаются в следующем.

Будем откладывать по оси ординат среднее пластовое давление, которое можно принять с большой точностью равным контурному давлению. По оси абсцисс будем откладывать насыщенность, также среднюю по пласту:



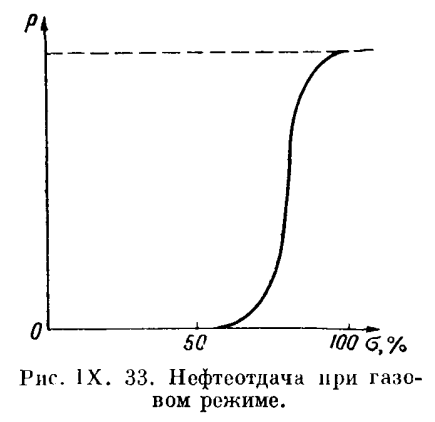
Рисунок 7. Нефтеотдача при газовом режиме.

Как следует из рисунка, когда давление падает до нуля, насыщенность не снижается ниже 60-70%. Это означает, что за счет энергии растворенного газа из пласта может быть отобрано только около 30% всего запаса.

К. А. Царевич также рассчитал изменение газового фактора в зависимости от времени при неустановившемся режиме растворенного газа.

Если откладывать по оси абсцисс время, а по оси ординат газовый фактор, то оказывается, что газовый фактор сначала растет, а потом падает.

---

Смотрите также файлы

• Диагностика и техническое обслуживание Системы смазки.docx

• Актуальность темы исследования. Правовое регулирование.docx

• Программа, программа.docx

• Инвестиционный климат г. Сызрань.docx

• Ранняя профилизация обучения как основа самоопределения обучающихся. Профориентация.ppt